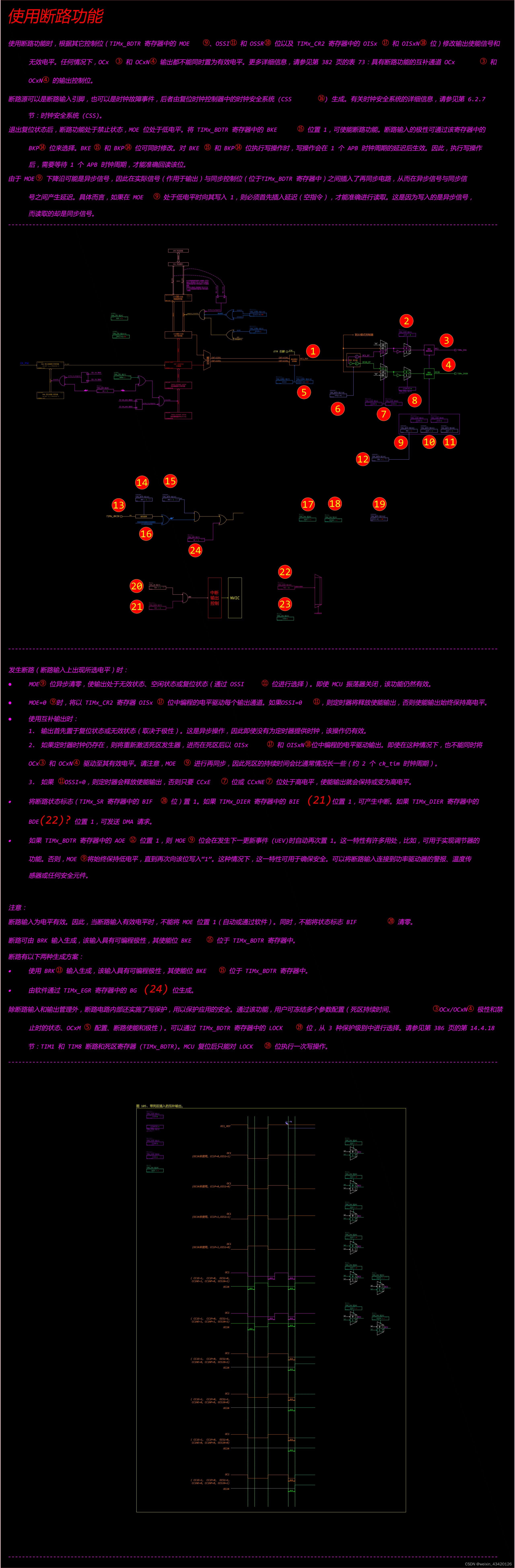
使用断路功能
使用断路功能时，根据其它控制位（TIMx_BDTR 寄存器中的 MOE⑨、OSSI⑪ 和 OSSR⑩ 位以及 TIMx_CR2 寄存器中的 OISx⑰ 和 OISxN⑱ 位）修改输出使能信号和无效电平。任何情况下，OCx③ 和 OCxN④ 输出都不能同时置为有效电平。更多详细信息，请参见第 382 页的表 73：具有断路功能的互补通道 OCx③ 和 OCxN④ 的输出控制位。
断路源可以是断路输入引脚，也可以是时钟故障事件，后者由复位时钟控制器中的时钟安全系统 (CSS⑯) 生成。有关时钟安全系统的详细信息，请参见第 6.2.7 节：时钟安全系统 (CSS)。
退出复位状态后，断路功能处于禁止状态，MOE 位处于低电平。将 TIMx_BDTR 寄存器中的 BKE⑮ 位置 1，可使能断路功能。断路输入的极性可通过该寄存器中的 BKP⑭ 位来选择。BKE⑮ 和 BKP⑭ 位可同时修改。对 BKE⑮ 和 BKP⑭ 位执行写操作时，写操作会在 1 个 APB 时钟周期的延迟后生效。因此，执行写操作后，需要等待 1 个 APB 时钟周期，才能准确回读该位。
由于 MOE⑨ 下降沿可能是异步信号，因此在实际信号（作用于输出）与同步控制位（位于TIMx_BDTR 寄存器中）之间插入了再同步电路，从而在异步信号与同步信号之间产生延迟。具体而言，如果在 MOE⑨ 处于低电平时向其写入 1，则必须首先插入延迟（空指令），才能准确进行读取。这是因为写入的是异步信号，而读取的却是同步信号。
---------------------------------------------------------------------------------------------------------------------------------------------

---------------------------------------------------------------------------------------------------------------------------------------------

发生断路（断路输入上出现所选电平）时：
●    MOE⑨ 位异步清零，使输出处于无效状态、空闲状态或复位状态（通过 OSSI⑪ 位进行选择）。即使 MCU 振荡器关闭，该功能仍然有效。
●    MOE=0 ⑨时，将以 TIMx_CR2 寄存器 OISx⑰ 位中编程的电平驱动每个输出通道。如果OSSI=0⑪，则定时器将释放使能输出，否则使能输出始终保持高电平。
●    使用互补输出时：
1.    输出首先置于复位状态或无效状态（取决于极性）。这是异步操作，因此即使没有为定时器提供时钟，该操作仍有效。
2.    如果定时器时钟仍存在，则将重新激活死区发生器，进而在死区后以 OISx⑰ 和 OISxN⑱位中编程的电平驱动输出。即使在这种情况下，也不能同时将 OCx③ 和 OCxN④ 驱动至其有效电平。请注意，MOE⑨ 进行再同步，因此死区的持续时间会比通常情况长一些（约 2 个 ck_tim 时钟周期）。
3.    如果 ⑪OSSI=0，则定时器会释放使能输出，否则只要 CCxE⑦ 位或 CCxNE⑦ 位处于高电平，使能输出就会保持或变为高电平。
·    断路状态标志（TIMx_SR 寄存器中的 BIF⑳ 位）置 1。如果 TIMx_DIER 寄存器中的 BIE(21)位置 1，可产生中断。如果 TIMx_DIER 寄存器中的 BDE(22)? 位置 1，可发送 DMA 请求。
·    ‚果 TIMx_BDTR 寄存器中的 AOE⑫ 位置 1，则 MOE⑨ 位会在发生下一更新事件 (UEV)时自动再次置 1。这一特性有许多用处，比如，可用于实现调节器的功能。否则，MOE⑨将始终保持低电平，直到再次向该位写入“1”。这种情况下，这一特性可用于确保安全。可以将断路输入连接到功率驱动器的警报、温度传感器或任何安全元件。

注意： 
断路输入为电平有效。因此，当断路输入有效电平时，不能将 MOE 位置 1（自动或通过软件）。同时，不能将状态标志 BIF⑳ 清零。
断路可由 BRK 输入生成，该输入具有可编程极性，其使能位 BKE⑮ 位于 TIMx_BDTR 寄存器中。
断路有以下两种生成方案：
·    用 BRK⑬ 输入生成，该输入具有可编程极性，其使能位 BKE⑮ 位于 TIMx_BDTR 寄存器中。
·    1软件通过 TIMx_EGR 寄存器中的 BG(24) 位生成。
除断路输入和输出管理外，断路电路内部还实施了写保护，用以保护应用的安全。通过该功能，用户可冻结多个参数配置（死区持续时间、③OCx/OCxN④ 极性和禁止时的状态、OCxM⑤ 配置、断路使能和极性）。可以通过 TIMx_BDTR 寄存器中的 LOCK⑲ 位，从 3 种保护级别中进行选择。请参见第 386 页的第 14.4.18 节：TIM1 和 TIM8 断路和死区寄存器 (TIMx_BDTR)。MCU 复位后只能对 LOCK⑲ 位执行一次写操作。
---------------------------------------------------------------------------------------------------------------------------------------------

---------------------------------------------------------------------------------------------------------------------------------------------