题目链接:ZZULIOJ
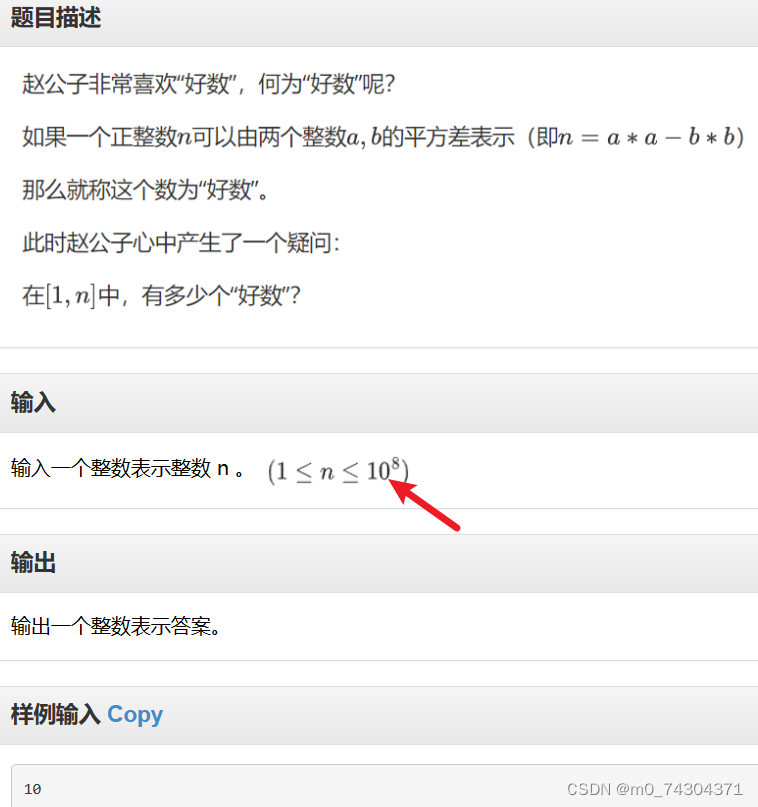
3110: 数(shu)数(shu)问题
分析:
看到这个题第一步想的是 先把每个平方数给求出来 然后枚举 但是时间复杂度大于1e8 交了一下TLE 但后来打表发现,好数太多了要是枚举的话 注定TLE 能不能间接的去做呢? 把不是的减去,那不就是好数了吗? 这个时候又是打表,会发现要是100以内的好数的话,2 6 10 14 22....不是好数 咱们分析 2 = 2 * 1, 6 = 2 * 3, 10 = 2 * 5, 14 = 2 * 7......so
代码:
#include<bits/stdc++.h>
using namespace std;
int n, m, ret = n;
signed main() {
cin >> n;
ret = n;
for(int i = 1, j = 1; 2 * i <= n; i = j * 2 + 1,++j, ret--) {}
cout << ret << endl;
return 0;
}3111: 点(dian)点(dian)问题

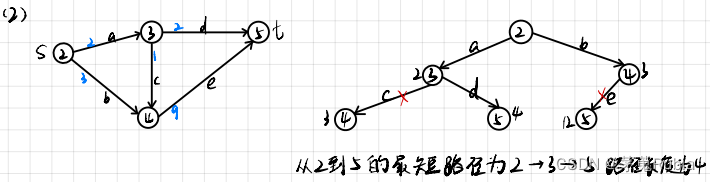
这个题的大致意思就是 在x轴上给你n个点, 让你求一个点x 使得这n个点到这个x的距离是最小的,问你最小的距离是多少?
分析:
这个题是一个典型的 绝对值贪心问题, 这个题的模板是 厂库选址的问题 ,结论是 选的那个点,就是给的这n个点(从小到大排序) 的中位点,也就是中间位置的那个点, 然后枚举这个n个点 ret += abs(a[i] - x) ret就是最后的答案
证明:
设最后选取的点是x 那么这n个点到x的距离就是 dis = |x1 - x| + |x2 - x| + ..... + |xn - x|
第一个和最后一个 第二个和倒数第二个 ..... 结合在一起 这里需要用到的是 |a - x| + |b - x| >= |a - b| 当且仅当 x在a和b的中间的时候 等号成立
因此 这个x只要 都在 每两两结合(第一个和最后一个 第二个和倒数第二个.......)的中间的话 就是最小的 那么 就是中位数那个点 就是最后选择的那个点
代码:
#include<bits/stdc++.h>
#define y1 Y1
#define fi first
#define endl "\n"
#define se second
#define PI acos(-1)
#define int long long
#define pb(x) push_back(x)
#define PII pair<int, int>
#define Yes cout << "Yes\n";
#define No cout << "No\n";
#define YES cout << "YES\n";
#define NO cout << "NO\n";
#define _for(i, a, b) for(int i = a; i <= b; ++i)
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
using namespace std;
const int N = 2e5 + 10;
int a[N];
int n, m, ret = 0;
string s;
signed main() {
IOS;
cin >> n;
_for(i, 1, n)cin >> a[i];
int t = a[(n + 2 - 1) / 2]; // a / b向上取整是 (a + b - 1) / b
for(int i = 1; i <= n; ++ i ) {
ret += abs(a[i] - t);
}
cout << ret << endl;
return 0;
}
/*
贪心问题:
设建在x的位置上 则 距离是
dis = |x1 - x| + |x2 - x| + ..... + |xn - x|
第一个和最后一个 第二个和倒数第二个 ..... 结合在一起 这里需要用到的是 |a - x| + |b - x| >= |a - b| 当且仅当x在a和b的中间的时候 等号成立
因此 这个x只要都在的话 就是最小的 那么 就是中位数那个点 就是答案
*/