目录
一、基于最大间隔分隔数据
二、寻找最大间隔
1. 最大间隔
2. 拉格朗日乘子法
3. 对偶问题
三、SMO高效优化算法
四、软间隔
五、SMO算法实现
1. 简化版SMO算法
2. 完整版SMO算法
3. 可视化决策结果
六、核函数
1. 线性不可分——高维可分
2. 核函数
七、垃圾邮件分类
八、总结
上次实验使用的logistic回归是一种线性分类模型,其基本思想是根据数据集训练出一个线性回归模型,再使用sigmoid函数将输出映射到0到1范围内,这个输出值就是样本预测为正例的概率,根据概率分类样本,因此logistic回归是根据所有数据样本来确定一个线性模型的。
这次实验实验的支持向量机(Support Vector Machines,SVM)和logistic回归很类似,SVM也是一种解决二分类问题的线性分类算法,与logistic回归不同的是,SVM分类只考虑样本分界线附近的样本点,即支持向量,其选择划分数据集的超平面是只根据支持向量来决定的,而logistic回归训练模型时所有样本都有参与计算,因此logistic回归是考虑所有样本点的。因此,它们的训练目标是不一样的,logistic回归是为了得到最拟合数据集的线性模型,而SVM是为了得到使支持向量之间间隔最大的超平面。
一、基于最大间隔分隔数据
我们先从一个简单的二维的数据集开始,这个二维数据集中的样本都分布在二维平面,其中“+”和“-”分别代表两种类别的样本。要划分下面这个数据集,我们需要一条能将正负样本区分隔开的直线。如下图所示。
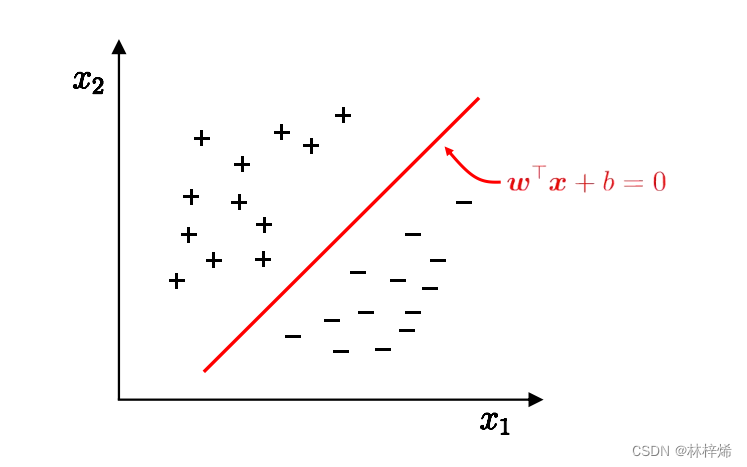
寻找一条划分数据集的直线很简单,但是会有一个问题,划分数据集的直线可以有很多条,我们究竟应该选择那一条直线呢?

我们直观看上去,肯定是选择红色的这条直线a0,而不是其他的直线,因为红色这条直线离正负样本的距离都较远,使用它作为划分直线能够很好的将正负样本分隔开。而对于其他的直线,它们离某一类的样本太接近了,这样的划分直线虽然在训练集上划分效果很好,但是遇到没见过的样本,它的预测性能就可能比较差了,比如很接近正样本的划分直线a1,它在训练集上能完全将正负样本区分开,但是如果遇到一个相对比较靠近负样本的样本,它实际上是正样本,但a1却会将其划分为负样本,对于划分直线a2也是一样。
我们希望得到的划分直线的容忍性好,鲁棒性好,泛化能力强,就需要选择一条使样本之间间隔最大的直线。
在二维数据集中,划分数据集的是一条直线,在三维数据集中,划分数据集的就得是平面了,那么再更高维的数据集中,应该使用什么对象来划分数据集呢?在高维数据集中,用来划分数据集的对象被称为超平面,也就是分类的决策边界。所有用来划分数据集的对象都可以称作超平面,包括二维的直线和三维的平面。
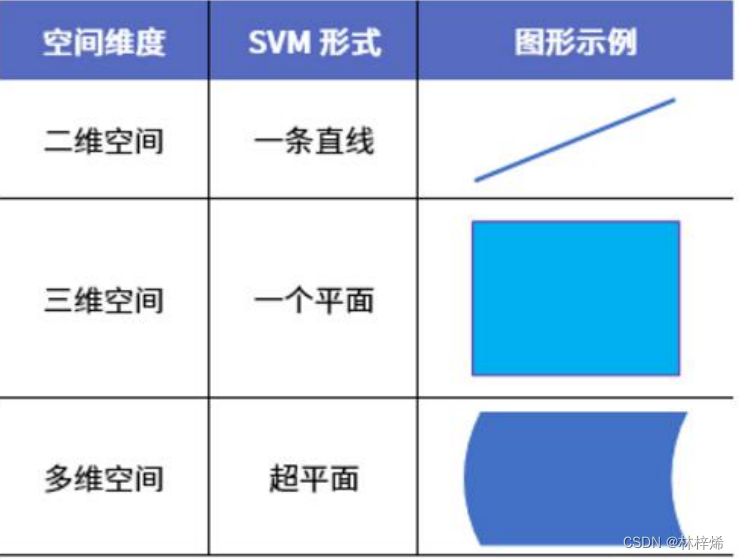
SVM的训练目标就是找到一个能最大化分类边界的超平面,用该超平面来分类预测样本。
二、寻找最大间隔
1. 最大间隔
既然支持向量机的目标是找到一个与正负样本间隔最大的超平面,那么首先我们需要知道间隔的表达式。
对于训练数据:
该数据集线性可分当且仅当:
,且
上式的w和x都是用向量来表示的,w={w1,w2,...,wn),x={x1,x2,...,xn}。
这里,我们使用的类别标签是-1和+1,而不是0和1,因为使用+1和-1我们可以通过一个统一的公式来表示间隔。
上式可以等价于:
上式中c是一个任意的正常数,我们可以将左右两边除以c,得到
而w和b是我们要求的参数,将其除以一个常数仍然还是参数w和b,因此可以上式写作
根据的取值,可以得到两个式子:
可以用两个超平面方程来表示
如下图所示。
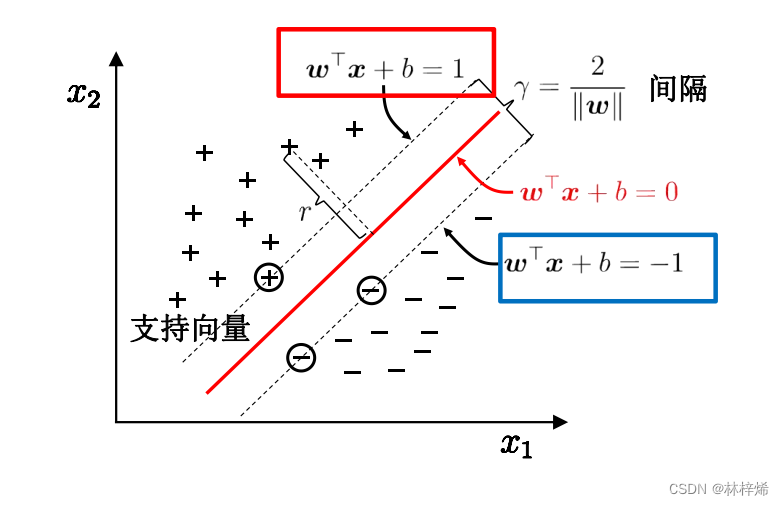
这样,在超平面之上的样本分类为正样本,在超平面
之下的样本分类为负样本,而我们要求的超平面的方程就是两个超平面中间的超平面
。最大化正负样本之间的间隔就变为了最大化超平面
和
之间的距离。
两个超平面之间的距离为:
从上图我们也能看出,SVM求解线性模型的时候是只考虑支持向量的,它要求的最大间隔也是支持向量之间的最大间隔,具体量化这个距离是根据支持向量到分隔超平面的距离计算的,需要计算的就是正负支持向量到分隔超平面的距离之和。
比如正例支持向量到分隔超平面的距离就是(w是超平面的法向量):
负例支持向量到到分隔超平面的距离与正例相同,而,那么分类间隔就是:
和上面计算的结果是一样的,感觉上面计算的更好理解一点。
现在,我们要求解的问题就变为寻找参数w和b,使得分类间隔最大:
我们可以将上式改为:
为什么改成而不是
呢?因为
在后面使用拉格朗日乘子法求解时比较方便,对w求导能得到w的表达式,便于计算。
下面使用一个简单的例子来计算求解最佳参数w,b。
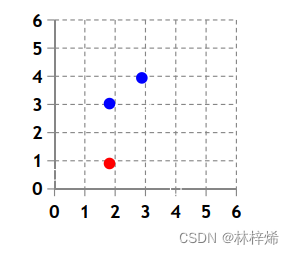
上面是一个简单的二维数据集,只包含三个样本,其中蓝色的是正样本,红色的是负样本。
我们要求解的是:
将上述三个样本点(2,3)、(3,4)、(2,1)代入方程,得到:
将上式消去b得到:
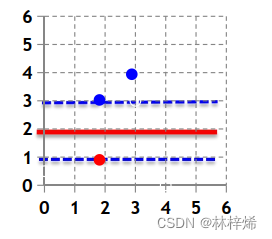
在系数坐标轴中画出两条直线和
。

上图中横坐标为x1,纵坐标为x2。
同时满足上述两式的点在图中浅蓝色区域内,我们需要的是在这个区域内寻找使得最小的参数w和b,
的最小值也就是
的最小值,
的最小值在坐标系中可以表示为点到原点的距离,我们可以做一个与这个区域范围下方相切的圆心为原点的圆,那么到原点距离最短的点就是切点,这个点的坐标是(0,1),也就是
。
把代入原本的三式可以得到:
根据上述三式可以得到:b=-2
最终得到的超平面方程为:
使用该超平面划分数据集,如下图。
上述是直接根据样本代入约束条件得到满足条件的参数范围,并从中寻找使得最小的参数w、b,这样的方法实现比较简单,但它有个问题,就是在高维的时候计算需要的样本也会很多,n维的数据集需要n+1个样本,得到n+1个方程,计算起来就比较麻烦了,而且这种方法计算的极小值点可能是不唯一的。因此我们需要使用其他的方法来求解问题。
2. 拉格朗日乘子法
拉格朗日乘子法是一种多元函数在变量受到条件约束时,求极值的方法,SVM求解的目标正好就属于这里问题,因此可以使用拉格朗日乘子法来求解问题。
给定一个目标函数,希望找到
,在满足约束条件g(x)=0的前提 下,使得f(x)有最小值。该约束优化问题记为:
可建立拉格朗日函数:
其中 λ 称为拉格朗日乘数。因此,可将原本的约束优化问题转换成等价的 无约束优化问题: 。
分别对待求解参数求偏导,可得:
一般联立方程组可以得到相应的解。
将约束等式 g(x)=0 推广为不等式 g(x)≤0。这个约束优化问题可改:
同理,其拉格朗日函数为:
其约束范围为不等式,因此可等价转换成Karush-Kuhn-Tucker(KKT)条件:
在此基础上,通过优化方式(如二次规划或SMO)求解其最优解。
3. 对偶问题
现在回到待求解问题上,我们的待求解问题是:
约束条件是,需要更改成下式:
接着引入拉格朗日乘子得到拉格朗日函数:
令对w和b的偏导为0:
得到:
原式可以写作:
将代入
可以得到:
化简得到:
这样原问题就转换为对偶问题了,得到的关系式是关于变量的,那么对这个式子,我们需要求的是
还是
。这个可以证明最后要求的目标是
,也就是:
根据KKT条件,可以得到如下的约束条件:
前面说过在超平面和
上的样本就是划分边界上的样本点,也就是支持向量,对应
,也就是说支持向量都满足关系式
,此时
。而对应其他不在划分边界上的点,
,又因为
,所以
,根据上面推导出的
,对于这类不在划分边界上的样本点,都有
,样本
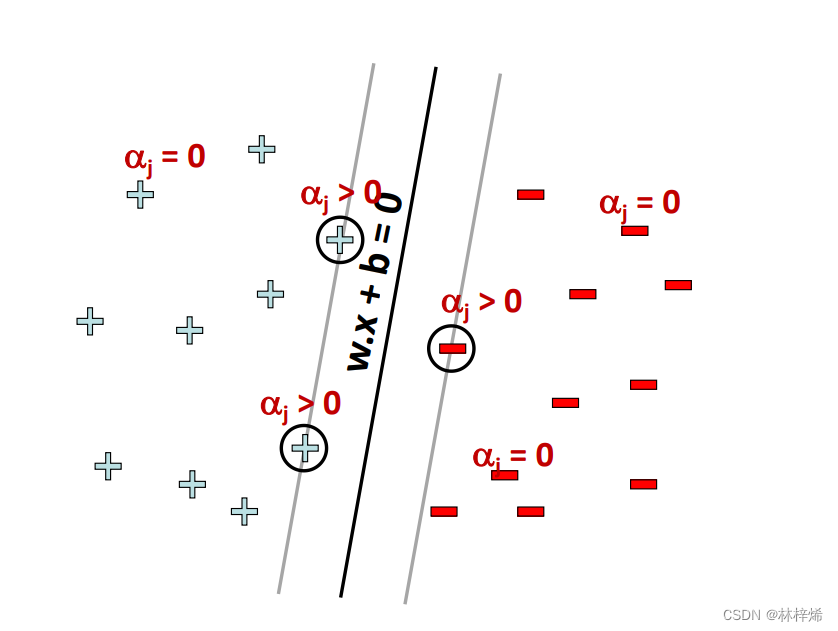
单项计算的结果为0,该样本对w的值没有贡献,也就是前面说的最终模型只与支持向量有关,其他样本都会被舍弃。如下图所示。
三、SMO高效优化算法
前面我们已经将原问题转换为对偶问题:
对于这个问题,我们该如何求解呢?对于这类二次规划问题的求解方法有很多,其中一种就是SMO算法,SMO表示序列最小优化(Sequential Minimal Optimization)。SMO算法是将大优化问题分解为多个小优化问题来求解的。这些小优化问题往往很容易求解,并且对它们进行顺序求解的结果与将它们作为整体求解的结果是完全一致的,同时总求解的时间还会短很多。
SMO算法的目标是求出一系列的和b,求出了这些
,就能根据对应的关系式得到权重w,也就能得到划分数据集的超平面了。
SMO算法的工作原理是:
1. 选取两个需要更新的变量
和
;
2. 固定
和
以外的参数,求解对偶问题更新
和
;
重复执行上述两个步骤直到模型收敛。
仅考虑和
时,对偶问题的约束条件变为:
更新公式为:
算法流程:

假设最优解为:
可得
根据w和b就能得到分隔超平面:
四、软间隔
前面的实现都有一个假设:数据100%线性可分,也就是能找到一个划分边界,使得数据集中的样本完全分类正确,这样的模型不允许有数据点处于分隔面的错误一侧。但实际上,一般的数据集都不会是100%线性可分的,都会或多或少存在一些不能正确分类的数据点,因此我们需要引入松弛变量和惩罚系数的概念。
原问题变为:
其中C是惩罚因子,用于控制“最大化间隔”和“保证大部分点的函数间隔小于1.0”这两个目标的权重。在优化算法的实现代码中,C是一个参数,可以通过调整C来得到不同的结果。
是松弛变量,作用是给限制条件加上一个值使得等式重新成立。
接着在使用拉格朗日乘子法构造目标函数:
将上式分别对w、b、求偏导,将得到的结果代入原式,就能得到对偶问题:
五、SMO算法实现
1. 简化版SMO算法
SMO算法的完整实现比较复杂,在此之前,我们先实现一个简化版的SMO算法,之后再实现完整版。
完整版SMO算法再外循环确定要优化的最佳alpha对,而简化版会跳过这个步骤,改为从遍历alpha集合中的每一个alpha值,然后在剩下的alpha集合中随机选取另一个alpha,从而构成alpha对。
在实现简化版SMO算法之前需要先定义三个辅助函数,分别用于读取数据集、随机选择alpha值、限制alpha值的范围。
# 读取数据集
def loadDataSet(filename):
dataSet = []
labelList = []
fp = open(filename)
lines = fp.readlines()
for line in lines:
lineSplit = line.strip().split()
dataSet.append([float(lineSplit[0]), float(lineSplit[1])])
labelList.append(float(lineSplit[2]))
return dataSet, labelList
# 随机选择alpha
def selectJrand(i, m):
j = i
# 随机选择一个下标不等于j的alpha的下标
while j == i:
j = int(random.uniform(0, m))
return j
# 限制alpha值的范围
def clipAlpha(aj, H, L):
if aj > H:
aj = H
if L > aj:
aj = L
return aj
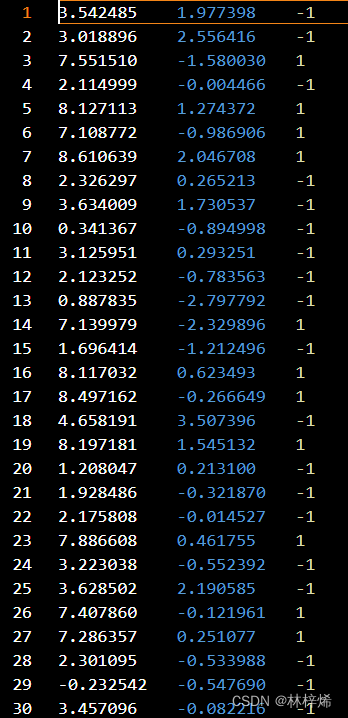
部分数据集:
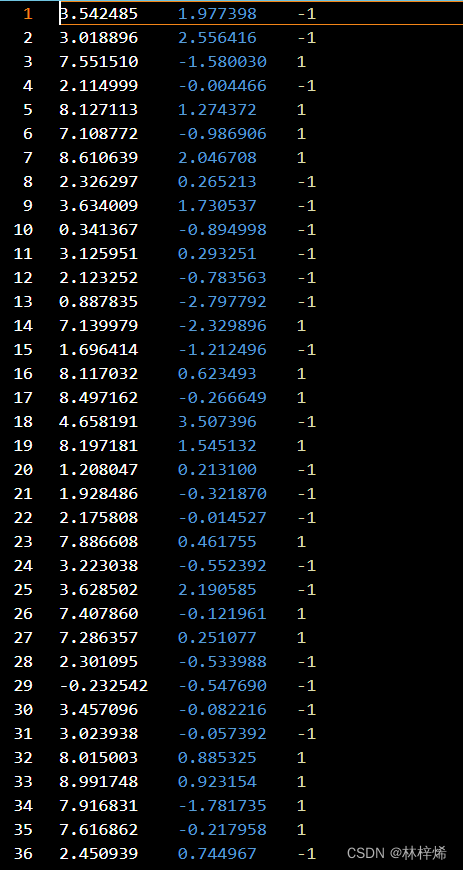
读取数据集:

SMO算法伪代码如下:
1. 创建一个alpha向量并初始化为全零;
2. 当迭代次数小于最大迭代次数时:
2.1. 对数据集中的每个数据向量:
2.1.1.判断该数据向量是否需要优化:
2.1.1.1. 随机选择另一个数据向量;
2.1.1.2. 同时优化这两个向量;
2.1.1.3. 如果两个向量都不能被优化,则退出内循环;
2.2. 如果所有向量都没有被优化,增加迭代数目,继续下一次循环;
代码实现如下:
# C:惩罚因子,toler:容错率,maxIter:最大迭代次数
def smoSimple(dataSet, classLabels, C, toler, maxIter):
dataSet = np.mat(dataSet)
classLabels = np.mat(classLabels).transpose()
b = 0
m, n = dataSet.shape
alphas = np.mat(np.zeros((m, 1)))
# 迭代次数
iter = 0
while iter < maxIter:
alphaPairsChanged = 0
for i in range(m):
fXi = float(np.multiply(alphas, classLabels).T * (dataSet * dataSet[i, :].T)) + b
Ei = fXi - classLabels[i]
# 判断是否要对该alpha值优化(误差超过容错率且alpha不等于0或C)
if classLabels[i] * Ei < -toler and alphas[i] < C \
or classLabels[i] * Ei > toler and alphas[i] > 0:
j = selectJrand(i, m)
fXj = float(np.multiply(alphas, classLabels).T * (dataSet * dataSet[j, :].T)) + b
Ej = fXj - classLabels[j]
# 需要使用copy复制一个数组,不然就是直接将对象赋值过去了,不会重新开辟空间
alphaIold = alphas[i].copy()
alphaJold = alphas[j].copy()
# 计算alpha值的范围,大于C和小于0的值都将调整为C和0
if classLabels[i] != classLabels[j]:
L = max(0, alphas[j] - alphas[i])
H = min(C, C + alphas[j] - alphas[i])
else:
L = max(0, alphas[j] + alphas[i] - C)
H = min(C, alphas[j] + alphas[i])
if L == H:
print("L == H")
continue
eta = 2. * dataSet[i, :] * dataSet[j, :].T - dataSet[i, :] * dataSet[i, :].T \
- dataSet[j, :] * dataSet[j, :].T
if eta >= 0:
print("eta >= 0")
continue
alphas[j] -= classLabels[j] * (Ei - Ej) / eta
# 限制alpha的值在L到H之间
alphas[j] = clipAlpha(alphas[j], H, L)
if abs(alphas[j] - alphaJold) < 0.00001:
print("j not moving enough")
continue
alphas[i] += classLabels[j] * classLabels[i] * (alphaJold - alphas[j])
b1 = b - Ei - classLabels[i] * (alphas[i] - alphaIold) * dataSet[i, :] * dataSet[i, :].T \
- classLabels[j] * (alphas[j] - alphaJold) * dataSet[i, :] * dataSet[j, :].T
b2 = b - Ej - classLabels[i] * (alphas[i] - alphaIold) * dataSet[i, :] * dataSet[j, :].T \
- classLabels[j] * (alphas[j] - alphaJold) * dataSet[j, :] * dataSet[j, :].T
if alphas[i] > 0 and alphas[i] < C:
b = b1
elif alphas[j] > 0 and alphas[j] < C:
b = b2
else:
b = (b1 + b2) / 2
alphaPairsChanged += 1
print("iter:", iter, "i:", i, 'pairs changed', alphaPairsChanged)
if alphaPairsChanged == 0:
iter += 1
else:
iter = 0
print('iteration number:', iter)
return b, alphas
上述代码首先将数据集dataSet和标签转换为矩阵,便于后续计算。随后进行迭代更新alpha,每次迭代遍历alpha值,对于每一个alpha值,先使用当前的模型计算样本xi的预测结果fXi,这个值是概率值,并不是真实的分类,将预测值与真实值相减得到预测误差Ei。随后进行判断是否要对该当前alpha值进行优化,预测误差超过容错率且alpha值不等于0或C就需要优化。
alpha优化过程为:随机选取另一个alpha ,计算xj样本的预测结果fXj和误差Ej,然后计算alpha值的最大范围,限制alpha值在0-C之内。根据
计算公式
计算
值。然后就可以更新
和
的值了,首先根据公式
计算
的新值,并限制其范围在0-C之内,如果
更新的值与原值相差小于一个很小的阈值(0.00001),那么说明
的更新跨度不够大,跳过当前循环。如果大于该阈值,就接根据公式
着更新
,最后再更新b。
测试:
调用简化版SMO函数计算结果,输出b、大于0的alpha值以及支持向量
dataSet, classLabels = loadDataSet(os.getcwd() + '/svm_data/data/testSet.txt')
b, alphas = smoSimple(dataSet, classLabels, 0.6, 0.001, 40)
print(b)
print(alphas[alphas > 0])
i = 0
for alpha in alphas:
if alpha > 0.:
print(dataSet[i], classLabels[i])
i += 1运行结果:

2. 完整版SMO算法
完整版SMO算法有多个函数都需要使用一些参数,可以将这些参数和函数封装成一个类,包含算法所要用到的各个数据以及完整版SMO算法所需要的各类函数。
完整版SMO算法在内循环,也就是alpha值的更改和代数运算的步骤与简化版SMO算法是一样的,它们之间的不同在于选择alpha的方式,也就是外循环。
完整版SMO算法在外循环中选择第一个alpha值,其选择alpha值的方式有两种,一种是在数据集上进行单遍扫描,另一种方式是在非边界alpha中实现单遍扫描,非边界alpha指的是那些不等于边界0或C的alpha值。完整版SMO算法在选择alpha值时会交替使用上述两种方法。
SMO算法需要的参数有:数据集:dataSet,类别标签:classLabels,惩罚因子:C,容错率:toler。
定义一个Svm类,包含上述数据对象:
class Svm:
def __init__(self, dataSet, classLabels, C, toler):
self.X = dataSet
self.labels = classLabels
self.C = C
self.toler = toler
self.m = dataSet.shape[0]
self.n = dataSet.shape[1]
self.alphas = np.mat(np.zeros((self.m, 1)))
self.b = 0
self.eCache = np.mat(np.zeros((self.m, 2)))
self.w = np.zeros((self.n, 1))接着需要定义三个辅助函数分别用于:计算误差E、选择alpha值、计算误差E并将误差值存入变量eCache中,这些类都要封装在类Svm中,作为Svm类的成员函数。
def calcEk(self, k):
fXk = np.multiply(self.alphas, self.labels).T * \
(self.X * self.X[k, :].T) + self.b
Ek = fXk - self.labels[k]
return Ek
def selectJ(self, i, Ei):
maxK = -1
maxDeltaE = 0
Ej = 0
self.eCache[i] = [1, int(Ei)]
validEcacheList = np.nonzero(self.eCache[:, 0].A)[0]
if len(validEcacheList) > 1:
for k in validEcacheList:
if k == i:
continue
Ek = self.calcEk(k)
deltaE = abs(Ei - Ek)
if deltaE > maxDeltaE:
maxK = k
maxDeltaE = deltaE
Ej = Ek
return maxK, Ej
else:
j = selectJrand(i, self.m)
Ej = self.calcEk(j)
return j, Ej
def updataEk(self, k):
Ek = self.calcEk(k)
self.eCache[k] = [1, int(Ek)]定义优化alpha值的函数,其计算步骤与前面实现的简化版SMO函数是一样的,只是不用传入各类参数,而是使用类中的数据成员。
def innerL(self, i):
Ei = self.calcEk(i)
# print(Ei)
# print(self.labels[i] * Ei)
if (self.labels[i] * Ei < -self.toler) and (self.alphas[i] < self.C) \
or (self.labels[i] * Ei > self.toler) and (self.alphas[i] > 0):
j, Ej = self.selectJ(i, Ei)
alphaIold = self.alphas[i].copy()
alphaJold = self.alphas[j].copy()
if self.labels[i] != self.labels[j]:
L = max(0, self.alphas[j] - self.alphas[i])
H = min(self.C, self.C + self.alphas[j] - self.alphas[i])
else:
L = max(0, self.alphas[j] + self.alphas[i] - self.C)
H = min(self.C, self.alphas[j] + self.alphas[i])
if L == H:
print("L == H")
return 0
eta = 2. * self.X[i, :] * self.X[j, :].T - self.X[i, :] * self.X[i, :].T \
- self.X[j, :] * self.X[j, :].T
if eta >= 0:
print('eta >= 0')
return 0
self.alphas[j] -= self.labels[j] * (Ei - Ej) / eta
self.alphas[j] = clipAlpha(self.alphas[j], H, L)
self.updataEk(j)
if abs(self.alphas[j] - alphaJold) < 0.00001:
print('j not moving enough')
return 0
self.alphas[i] += self.labels[j] * self.labels[i] * (alphaJold - self.alphas[j])
self.updataEk(i)
b1 = self.b - Ei - self.labels[i] * (self.alphas[i] - alphaIold) \
* self.X[i, :] * self.X[i, :].T - self.labels[j] \
* (self.alphas[j] - alphaJold) * self.X[i, :] * self.X[j, :].T
b2 = self.b - Ej - self.labels[i] * (self.alphas[i] - alphaIold) \
* self.X[i, :] * self.X[j, :].T - self.labels[j] \
* (self.alphas[j] - alphaJold) * self.X[j, :] * self.X[j, :].T
if self.alphas[i] > 0 and self.alphas[i] < self.C:
self.b = b1
elif self.alphas[j] > 0 and self.alphas[j] < self.C:
self.b = b2
else:
self.b = (b1 + b2) / 2
return 1
else:
return 0完整版SMO算法,同时也是外循环代码,在外循环中选取alpha值,接着调用内循环函数innerL优化alpha值。
def smoP(self, maxIter, kTup=('lin', 0)):
iter = 0
entireSet = True
alphaPairsChanged = 0
while iter < maxIter and (alphaPairsChanged > 0 or entireSet):
alphaPairsChanged = 0
if entireSet:
for i in range(self.m):
alphaPairsChanged += self.innerL(i)
print('fullset, iter:', iter, 'i:', i, 'pairs changed', alphaPairsChanged)
iter += 1
else:
nonBoundIs = np.nonzero((self.alphas.A > 0) * (self.alphas.A < self.C))[0]
for i in nonBoundIs:
alphaPairsChanged += self.innerL(i)
print('non-bound, iter:', iter, 'i:', i, 'pairs changed', alphaPairsChanged)
iter += 1
if entireSet:
entireSet = False
elif alphaPairsChanged == 0:
entireSet == True
print('iteration number:', iter)
# 根据训练得到的alphas计算权重
for i in range(self.m):
self.w += np.multiply(self.alphas[i] * self.labels[i], self.X[i, :].T)该函数会交替使用使用两种选择alpha值的方式,在entireSet为True的时候使用在整个数据集上选取alpha值的方法,在entireSet为False的时候选择在非边界alpha选择alphaz值的方法,在使用过整个数据集选取的方法后就会置entire为False,如果有任意一对alpha值改变,下一次循环就会选择非边界alpha选取方法,如果没有alpha更改,则下一次仍会选择在整个数据集上选取的方法。
smoP函数可以看作是训练函数,调用该函数就能计算得到最佳参数w和b,为了方便,该函数没有直接返回w和b,而是将其保存在类中。
得到训练后的模型参数后就可以输入样本进行预测了,我们需要定义一个分类函数。
# 对一维数据分类
def classfy1(self, tdata):
tdata = np.mat(tdata)
y_hat = tdata * np.mat(self.w) + b
if y_hat > 0:
return 1
if y_hat < 0:
return -1
# 对二维数据分类
def classfy2(self, tdatas):
tdatas = np.mat(tdatas)
y_hat = tdatas @ np.mat(self.w) +b
y_hat[y_hat > 0] = 1
y_hat[y_hat < 0] = -1
return np.array(y_hat)这里我定义了两个分类函数,一个是对一维数据进行分类(单个样本),另一个是对二维样本进行分类(多个样本) 。一维数据直接套公式就能得到结果,然后将大于0的结果分类为1,小于0的结果分类为-1。二维数据需要使用矩阵进行计算,计算后使用y_hat[y_hat > 0]和y_hat[y_hat < 0]分别取大于0和小于0的预测结果,将其分别赋值为1和-1。
单样本分类:
svm = Svm(np.mat(dataSet), np.mat(classLabels).transpose(), 0.6, 0.001)
svm.smoP(40)
zzx = svm.classfy1(dataSet[0])预测结果:

多样本分类:
svm = Svm(np.mat(dataSet), np.mat(classLabels).transpose(), 0.6, 0.001)
svm.smoP(40)
svm.classfy2(dataSet)
数据集:
3. 可视化决策结果
如果想更直观的观察分类的结果,我们可以使用绘图工具将分类结果可视化。
def plot_data(ax, X, y):
dataS = np.concatenate((np.array(X), np.array(y).reshape(-1, 1)), axis=1)
'''绘制数据集的散点图'''
ax.scatter(dataS[dataS[:, -1] == 1, :][:, 0], dataS[dataS[:, -1] == 1, :][:, 1], s=30, marker='x', label='Positive', c='black')
ax.scatter(dataS[dataS[:, -1] == -1, :][:, 0], dataS[dataS[:, -1] == -1, :][:, 1], s=30, marker='o', label='Negative', c='y')
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_title('Example Dataset 1')
ax.legend()
def plot_boundary(ax, clf, X):
'''绘制超平面'''
x_min, x_max = X[:, 0].min() * 1.2, X[:, 0].max() * 1.1
y_min, y_max = X[:, 1].min() * 1.1, X[:, 1].max() * 1.1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 500), np.linspace(y_min, y_max, 500))
# Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = clf.classfy2(np.c_[xx.ravel(), yy.ravel()])
print('Z', Z.shape)
Z = Z.reshape(xx.shape)
ax.contour(xx, yy, Z)测试:
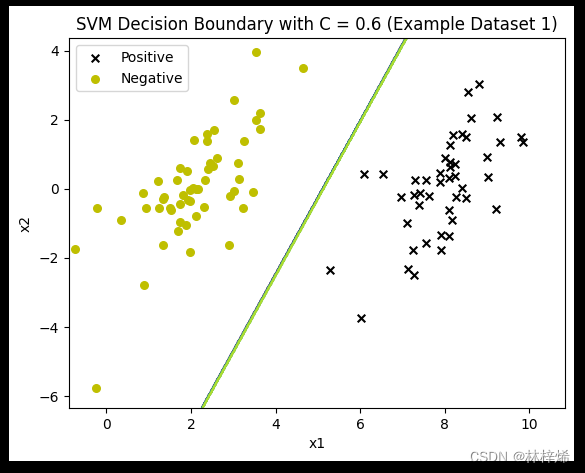
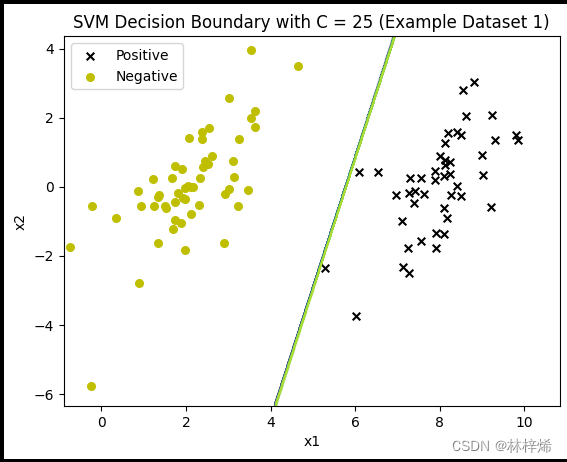
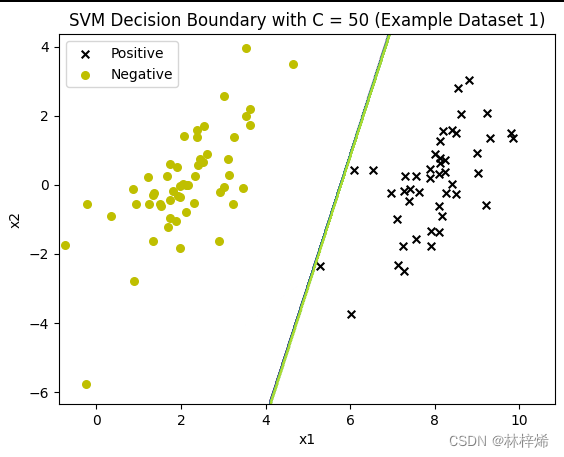
测试不同惩罚因子C的分类结果
X_np = dataSet
y = classLabels
for c in [0.6, 25, 50]:
modela = Svm(np.mat(X_np), np.mat(y).transpose(), c, 0.001)
modela.smoP(40)
fig, ax = plt.subplots()
plot_data(ax, X_np, y)
plot_boundary(ax, modela, np.array(X_np))
ax.set_title('SVM Decision Boundary with C = {} (Example Dataset 1)'.format(c))
plt.show()运行结果:
不知道为什么这个多次运行有多种结果,正常应该是C越小越松弛,能容许的错误分类数越多,C越大能允许的错误分类越少。这个数据集没有不能被正确分类的样本,所以看不出来不同C值带来的不同结果。
我换了另一个有不能被正确分类的样本的数据集来测试,这个数据集是.mat格式的,好像是二进制文件,我不知道怎么打开,不知道里面是什么数据。一开始运行的时候负样本一个都不显示。
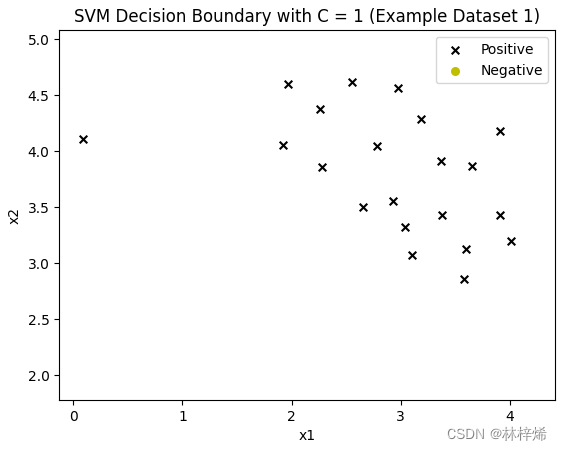
后面看了一下这个数据集的类别标签是0和1,但是上面定义的Svm模型处理的类别标签是-1和1,所以需要将类别标签0改为-1。
raw_data = loadmat(os.getcwd() + '\svm_data\data\ex6data1.mat')
data = pd.DataFrame(raw_data['X'], columns=['X1', 'X2'])
data['y'] = raw_data['y'].flatten()
X_np = data[['X1', 'X2']].values
y = data['y'].values.astype('float')
y[y == 0] = -1
print(y)
c = 20
modela = Svm(np.mat(X_np), np.mat(y).transpose(), c, 0.001)
modela.smoP(40)
fig, ax = plt.subplots()
plot_data(ax, X_np, y)
plot_boundary(ax, modela, np.array(X_np))
ax.set_title('SVM Decision Boundary with C = {} (Example Dataset 1)'.format(c))
plt.show() 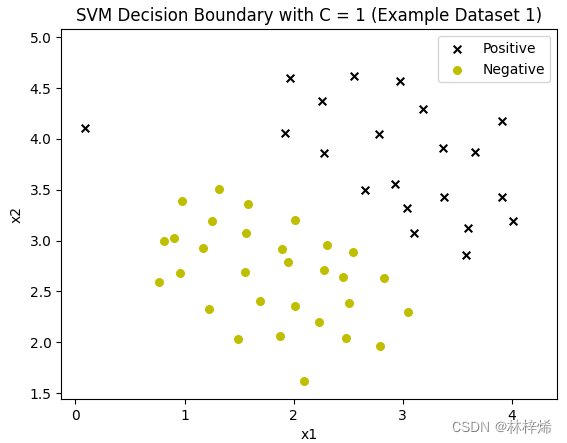
运行后虽然负样本出来了,但是分隔线却没了,应该是在坐标轴下面了,多运行几次有时候会出来,但是也是个很差的分隔线,不知道为什么在这个数据集上运行的结果这么差。
没办法我只能用库函数了,用库函数就能正确分类了。

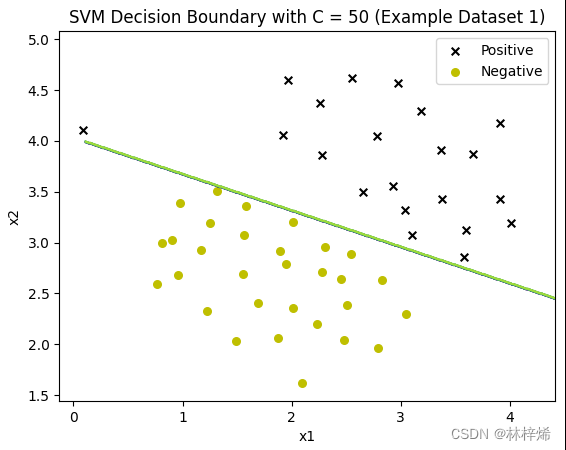
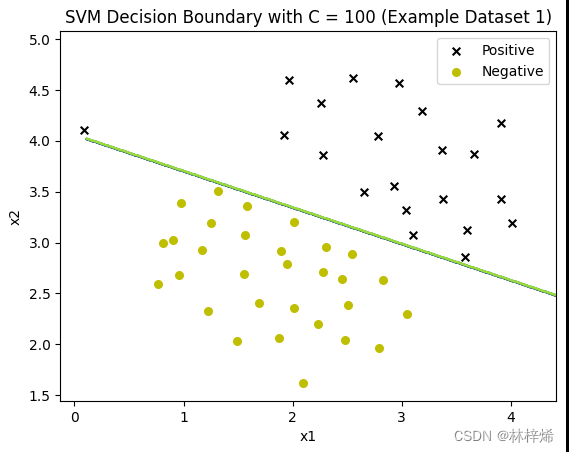
可以看出,C越小就越允许更多的样本被错误分类,第一张图中有一个更靠近负例的正样本,分割线能容许这样的样本存在,因此没有过于要求将这个样本也分类到正例,这样分类的结果就比较好。而下面两张图C比较大,会更倾向于将所有样本都正确分类,得出的结果反而不好。一般数据集中都会存在一些很难正确分类的样本,适当降低C的值效果会比较好。
六、核函数
1. 线性不可分——高维可分
前面计算求解的前提都是数据集线性可分,如果数据集线性不可分,也就不存在一个能正确划分两类样本的分隔超平面,此时应该怎么做?
我们可以将样本从原始特征空间映射到一个更高维的特征空间中,使得样本在这个高维的特征空间中线性可分。
如下图左边的二维特征空间中,找不到一条能准确划分数据集的直线,此时就可以将样本映射到高维空间中,如右图。在右图中就能找到一个能准确划分数据集的平面了。

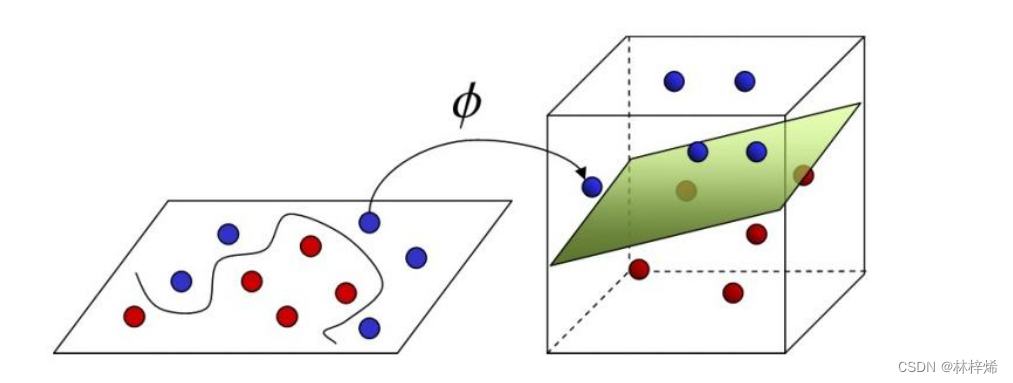
具体映射方法如下:
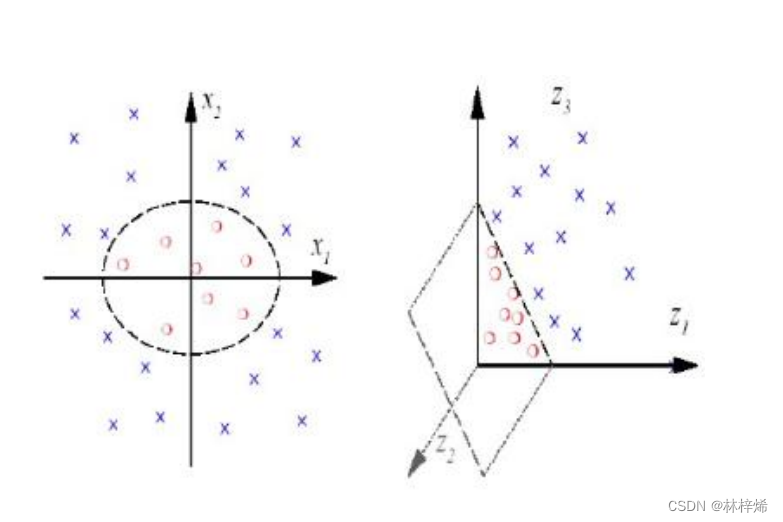
对于左图,无法找到一条能准确划分数据集的直线,但可以使用一个圆来划分。
圆的方程为:
变换:,将其映射到三维空间,得到:
变换得到的就是三维空间中的一个平面,使用该平面就能准确划分数据集了。
使用核函数后,原问题:
就变换为:
,只以内积的形式出现
线性模型变换为:
2. 核函数
将原始空间中的向量作为输入向量,并返回特征空间(转换后的数据空间,可能是高维)中向量的点积的函数称为核函数。
核函数定义如下:
根据Mercer定理:只要对称函数值所对应的核矩阵半正定, 则该函数可作为核函数。
常用的核函数有:

可视化决策:
def plot_data(X, y, ax):
'''绘制数据集的散点图'''
positive = data[data['y'] == 1]
negative = data[data['y'] == 0]
ax.scatter(positive['X1'], positive['X2'], s=20, marker='x', label='Positive', c='black')
ax.scatter(negative['X1'], negative['X2'], s=20, marker='o', label='Negative', c='y')
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.legend()
def plot_boundary(ax, clf, X):
'''绘制决策边界'''
x_min, x_max = X[:, 0].min() * 1.2, X[:, 0].max() * 1.1
y_min, y_max = X[:, 1].min() * 1.1, X[:, 1].max() * 1.1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 500), np.linspace(y_min, y_max, 500))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
ax.contour(xx, yy, Z)
测试:
import matplotlib.pyplot as plt
import pandas as pd
from scipy.io import loadmat
from sklearn import svm
raw_data = loadmat(os.getcwd() + '\svm_data\data\ex6data2.mat')
X, y = raw_data['X'], raw_data['y'].ravel() # 确保 y 是一维数组
data = pd.DataFrame(raw_data['X'], columns=['X1', 'X2'])
data['y'] = y
sigmax = [0.1, 0.2, 0.5]
for sigma in sigmax:
gamma = np.power(sigma, -2)
clf = svm.SVC(C=1, kernel='rbf', gamma=gamma)
model = clf.fit(X, y)
fig, ax = plt.subplots()
plot_data(X, y, ax)
plot_boundary(ax, model, X)
ax.set_title('SVM Decision Boundary with σ = {}'.format(sigma))
plt.show()运行结果:
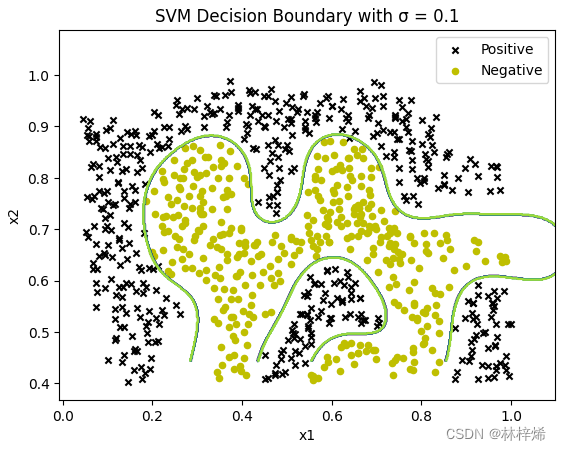


可以看出,sigma的值越大,绘制出的决策边界就会越平滑,但是不能很好的将两组数据划分出来,划分的精确度比较低,较大大的sigma值,得出的是一种大致的分隔边界,会有比较多的样本被错误分类,容易造成欠拟合的情况。当sigma的值比较小时,模型能很好的将两类样本分隔开,在训练集上的精确度很高,但这样泛化能力就比较差了,在测试集上的预测能力可能就比较差了,也就是产生过拟合的情况。
七、垃圾邮件分类
垃圾邮件数据集包含训练集和测试集,使用loadmat函数分别读取训练集和测试集并从中按对应标签取出特征向量和类别标签,使用径向基核构建svm分类器。
将模型训练好后进行预测,将预测结果与实际标签比较计算错误率。
train_data = loadmat(os.getcwd() + '\svm_data\data\spamTrain.mat')
test_data = loadmat(os.getcwd() + '\svm_data\data\spamTest.mat')
XTrain, yTrain = train_data['X'], train_data['y'].ravel() # 确保 y 是一维数组
XTest, yTest = test_data['Xtest'], test_data['ytest'].ravel()
sigma = 0.4
gamma = np.power(sigma, -2)
svc = svm.SVC(C=1, kernel='linear', gamma=gamma)
svc.fit(XTrain, yTrain)
y_predict = svc.predict(XTest)
errorRate = sum(y_predict != yTest) / len(yTest)
print('错误率为:', errorRate)运行结果:

这个错误率有点高,换了些其他的sigma值测试还是这个错误率。可能这个数据集是线性可分的,不用核函数。
将svm分类器的内核改为线性核linear:
svc = svm.SVC(C=1, kernel='linear')运行结果:
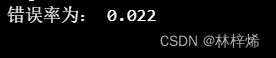
这个错误率就很低了。
八、总结
支持向量机也是一种线性分类模型,它通过寻找不同类别样本之间的最大间隔从而得到最佳的模型参数w和b,模型训练目标是计算得到一个最佳一个超平面,该超平面能够最大化支持向量之间的间隔,模型训练的时候只会考虑支持支持向量。支持向量之间的间隔可以计算得到是,使用拉格朗日乘子法将其转换到对偶问题,通过求解对偶问题来得到原问题的解。对偶问题的求解一般采用SMO算法来实现,SMO算法的基本思想就是每次选取两个α进行更新,根据对应的公式优化更新α参数,得到最佳的α值后再根据α计算w,再计算b,最后得到训练好的线性模型,使用该模型就能进行预测了。在遇到线性不可分的数据集时,可以使用核函数将样本映射到高维空间中,在高维空间求解。








![[自动化运维工具]ansible简单介绍和常用模块](https://img-blog.csdnimg.cn/direct/a6256d5bae7e47b390d03ed6d3eb3ca3.png)

