目录

🌈前言：

📁 什么是进制转换：

📁其他进制转换成十进制：

📂二进制( B ) ——> 十进制( D )

📂八进制( O ) ——> 十进制( D )

📂十六进制( H ) ——> 十进制( D )

📁十进制转换成其他进制

📁N进制转换成M进制：

📁代码展示：

📜总结：

 

---

🌈前言：

 

        不知道你平常遇到进制之间转换问题是否会头疼，博主我本人遇到进制转换问题非常头疼，不知所以云，上网上搜资料也是官话一堆，难以理解，但好在，经过我不断的努力，终于学会了，所以我写下这篇文章，希望能帮助更多像我这样的人。

        本篇文章是从零开始讲解进制，再用代码实现，如果你已经有了相关的知识储备，可以直接跳转到代码展示，本版本使用C++语言，但你并不需要担心，与C语言的不同只在于输入输出的形式（cin 写成scanf  cout写成printf即可）

---

• 📁 什么是进制转换：

        在日常生活中，我们处处用到进制，简单来说，进制就是计数的一种方法，比如我们数学问题，1+1这样简单的问题，他就是用10进制表示的；相信你也知道，在计算机中机器是用二进制来表示的，计算机底层就是一串串0和1组成的。

        这就涉及不同进制之间转换的问题了，如何将我们日常生活中用到的进制转换成另外一种进制呢。        

---

• 📁其他进制转换成十进制：

        有人就发现了规律，按权相加法，这是一种将N进制转换成10进制的一种方法。所谓的劝就是“位权”，如果你不理解，就可以认为是位置拥有的权利，比如十进制的个位，十位，百位等等，这就是权，个位的权重是10^0（10的0次方），十位就是10^1意思类推。权重的指数是从0开始的，从右向左递增。

        按权相加，顾名思义，就是每一位×它的权重相加，得出来的数就是十进制数字。这里我们以二进制举例：

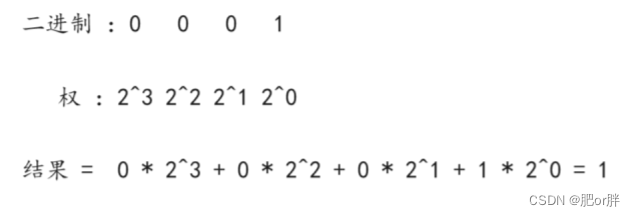
• 📂二进制( B ) ——> 十进制( D )

        上面你对权重有了了解，那我们来练练手吧。我们先从二进制开始。

1 (B) 的十进制表示为 =  1（D）

    1的权重是2^0，1 * 2^0 = 1

 

10（B）的十进制表示为 = 2（D）

    0的权重是2^0, 1的权重是2^1，结果 = 0 * 2^0 + 1 * 2^1 = 2;

 

11（B）的十进制表示为 = 3（D）

    左边第一个1的权重是2^0,右边1的权重是2^1, 结果 = 1 * 2^0 + 1 * 2^1 = 3；

        进过上面简单的计算，相信你一定会了简单的二进制转换为十进制，当然也别骄傲，后面还有小数位等着你，这一部分这篇文章就不做讲解了，如果感兴趣，可以度娘一下，或者评论区留言，我会进行答复。

 

• 📂八进制( O ) ——> 十进制( D )

       首先，我们先来讲解一下，什么是八进制，八进制就是逢八进一，也就是说每一位最多的取值就是0~7区间内，若果等于8向进一位。

        接下来，我们来看一下八进制如何转换成十进制，有了二进制基础的你，相信一定不成问题。

7（O）转换成十进制 = 7（D）

    7的权重是8^0 , 结果 = 7 * 8^0 = 7;

 

10（O）转换成十进制 = 8（D） 

    0的权重是8^0,1的权重是8^1 , 结果 = 0 * 8^0 + 1* 8^1 = 9

 

17（O）转换成十进制 = 15 （D） 

 

• 📂十六进制( H ) ——> 十进制( D )

        十六进制就是，逢十六进一。也就是说，每一位的取值是0~15区间内，但要注意的是，10~15不用数字表示，而是用A  B  C  D  E  F表示。当然并没有规定是用大写还是小写。

F（H）转换成十进制 = 15（D）

    F=15，结果 = 15 * 16^0 = 15;

 

1F（H）转换成十进制 = 31（D）

    结果 = 1 * 16^1 + 15 * 16^0 = 31；

        以上我们对不同进制转换成十进制有了一定的了解，接下来我们来看一下十进制如何转换成其他进制。

---

• 📁十进制转换成其他进制

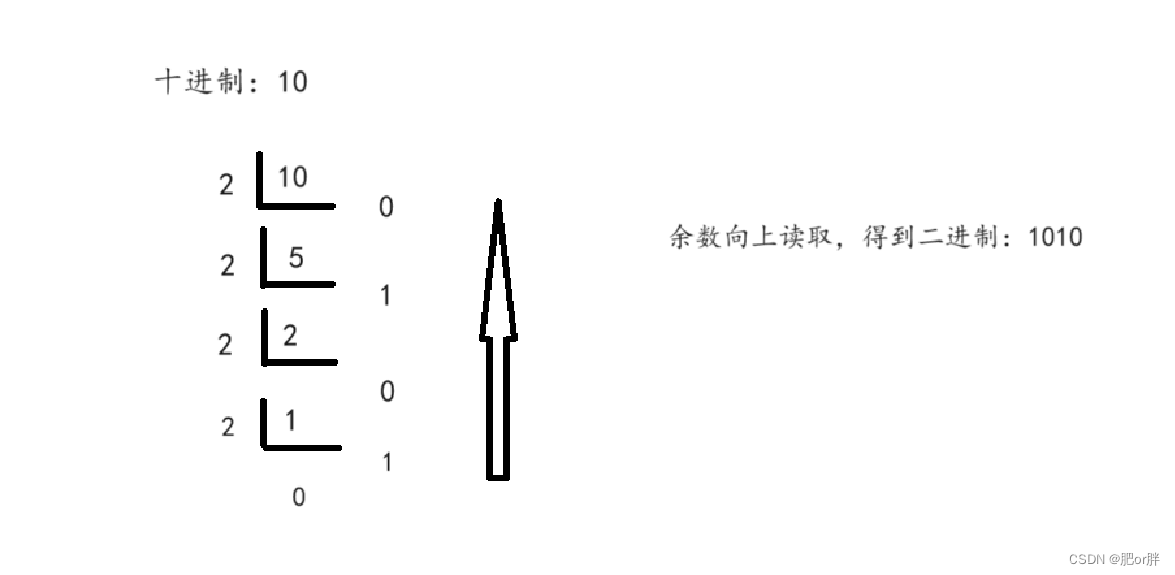
        这里就要介绍 “整数除以进制，直到不能相除，向上读取余数”，这里我们还是以十进制与二进制之间的转换为例，如下图。

        同样的道理，十进制转八进制，十六进制是一样的道理，只不过除数改为了8。

---

• 📁N进制转换成M进制：

        可能有的同学一看到这里就很头痛了，我才刚刚学会十进制与其他进制的转换，其他进制之间的转换这对我太难了。其实这并不难，我们只要将N进制转换成我们所熟悉的十进制，再转换成M进制不就简单了吗。

        这里扩充一个点，作为中间的转换进制，并不一定是十进制，也可以是二进制，但为了简单，适合更多的同学，所以这里将延续上面的讲解，使用十进制作为中间进制。同样，下面的代码展示，我们也是使用十进制作为中间进制。

---

• 📁代码展示：

input（输入）：

 进制 n  

 进制为n的数

 进制 m

output（输出）：

转换成进制为m的数

 

例如：

输入：16 

            F

           10

输出：15

        下面分批次介绍各个函数，先从主函数开始，最后展示完整代码。

//主函数
int main()
{
	int n, m, ten = 0;
	char num[100000] = { 0 };
	cin >> n;
	cin >> num;
	cin >> m;
	ten = N_To_Ten(num,n);

	char ans[100000] = { 0 };
	
	int k = Ten_To_M(num, ans,ten,m);

	//打印
	for (int i = k - 1;i >= 0;i--)
	{
		cout << ans[i];
	}
	return 0;
}

        这里我们首先定义一个足够大的字符数组num，用来存放进制为n的数，我们在封装一个函数，将这个数组中的每个数转换成十进制数。其次在封装一个函数，将字符数组转换后的十进制数转换成M进制，存放到字符数组ans中。

        ten ：十进制数

        k ：ans中数据个数，即转化成m进制的数据后，这个数据有几位。

//n 进制 --> 10进制
int N_To_Ten(char num[],int n)
{
	int ten = 0;
	int k = 0;	//权重
	for (int i = strlen(num) - 1;i >= 0;i--, k++)
	{
		if (num[i] >= 'A' && num[i] <= 'Z')
		{
			num[i] = num[i] - 'A' + 10;
		}
		else
		{
			num[i] = num[i] - '0';
		}
		ten = ten + num[i] * pow(n, k);
	}
	return ten;
}

//10进制 --> m进制
int Ten_To_M(char ans[],int ten,int m)
{
	int k = 0;
	while (ten != 0)
	{
		int temp = ten % m;
		ten /= m;
		if (ten >= 10 && ten <= 15)
		{
			ans[k++] = temp + 'A' - 10;
		}
		else
		{
			ans[k++] = temp + '0';
		}
	}
	return k;
}

        上面的内容最难理解可能就是 num[i] +- 'A'  +- 10了吧，这里讲解一下，这里就是+将字符'A'转换成整数，10,11等等，反之-就是将整数转换成字符A B C等等。这是针对十六进制进行的判断。

        同样的道理，+ - ‘0’也是如此。都是将字符转换成整数，整数转换成字符。例如八进制，二进制等。

 

---

• 📜总结：

        以上我们便从零基础开始讲解，什么是进制，十进制如何转换成其他进制，其他进制如何转换成十进制，了解了N进制转换成M进制，就是现将N进制转换成十进制，十进制再转换成M进制。作为中间进制，不仅可以是十进制，也可以是二进制等等，你熟悉那种转换方法，觉得哪种用起来编程方便，就用那种即可。

        以上，我们边对进制之间的转换做了总结复习，如果你觉得有用，欢迎点赞收藏关注，也欢迎大家在评论区讨论交流，指出我的错误。