图像梯度
- 前言
- Sobel算子
- 算子的定义
- Sobelx效果演示
- Sobely效果演示
- 完整轮廓
- 直接计算
- 复杂图片的轮廓
- Scharr算子与laplacian算子
- scharr算子的定义
- laplacian算子定义
- 三种算子的效果对比
- 结尾
前言
前面的文章中我们介绍了用膨胀和腐蚀得到了图像轮廓,图像梯度也是一种可以得到图像轮廓的方式,同时他也是边缘检测的其中一个步骤,下面我们来介绍各种可以求得图像梯度的算子。
假设我们有这样一张名为water.jpg的水元素图片

首先我们读出灰度图并进行二值化
img = cv2.imread('water.jpg',cv2.IMREAD_GRAYSCALE)
ret, img = cv2.threshold(img, 220, 255, cv2.THRESH_BINARY)
为了方便展示我们先创建一个显示图片的函数
def cv_show(img,name):
cv2.imshow(name,img)
cv2.waitKey()
cv2.destroyAllWindows()
Sobel算子
算子的定义
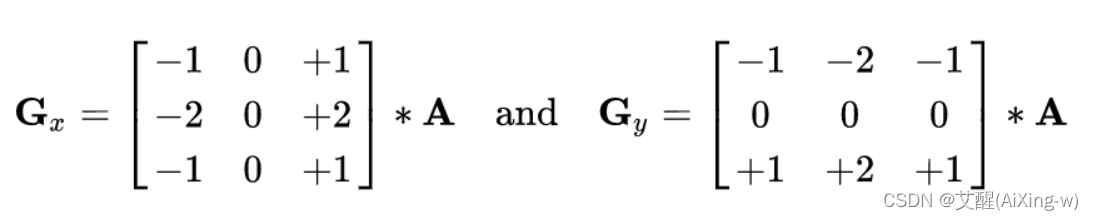
在opencv中可以使用cv2.Sobel使用sobel算子进行梯度计算
参数:cv2.Sobel(src, ddepth, dx, dy, ksize)
| 参数 | 含义 |
|---|---|
| ddepth | 图像的深度 |
| dx和dy | 分别表示水平和竖直方向 |
| ksize | Sobel算子的大小 |
Sobelx效果演示
当第3个参数为1,第4个参数为0时进行Gx操作,其中的A为待处理的图像在卷积核中待处理的区域
Gx操作所使用的算子可以直观的看出来更加注重像素点的左右方向,如果左侧黑右侧白,那么求得的值就是正值反之则是负值
sobelx = cv2.Sobel(img,cv2.CV_64F,1,0,ksize=3)
cv_show(sobelx,'sobelx')

我们可以发现轮廓并不完整,这是为什么呢,因为sobelx算子在左黑右白为正值,左白右黑为负值,而opencv自动将负值设成0,所以负值的边界在显示时会消失,但是实际上sobelx这个变量中负值的数值还是存在的,那么我们来进行一些操作让他显示出来,为了方便显示我们还是在原图上进行轮廓的绘制
sobelx = cv2.Sobel(img,cv2.CV_64F,1,0,ksize=3)
idx1, idx2 = np.where(sobelx<0)
idx3, idx4 = np.where(sobelx>0)
idx5, idx6 = np.where(sobelx!=0)
water = cv2.imread('water.jpg')
water_1 = water.copy()
water_2 = water.copy()
water_3 = water.copy()
water_1[idx1,idx2,:]=(0 ,0, 255)
water_2[idx3,idx4,:]=(0 ,255, 0)
water_3[idx5,idx6,:]=(255 ,0, 0)
cv_show(np.hstack([water_1, water_2, water_3]),'sobelx')

那么如果我们还是想得到之前那种黑白的轮廓图要如何处理呢
我们可以使用cv2.convertScaleAbs函数将sobelx的值取绝对值
sobelx_1 = cv2.Sobel(img,cv2.CV_64F,1,0,ksize=3)
sobelx_1 = cv2.convertScaleAbs(sobelx_1)
cv_show(sobelx_1,'sobelx')

我们可以看到。整个轮廓都是左右两侧,上下均有间断,这是为什么呢,因为Gx操作只针对左右,而不针对上下,要想得到上下的轮廓我们需要使用Gy操作
Sobely效果演示
当dx=0,dy=1时
sobely = cv2.Sobel(img,cv2.CV_64F,0,1,ksize=3)
sobely = cv2.convertScaleAbs(sobely)
cv_show(sobely,'sobely')

这次的间断变成了左右两侧
完整轮廓
我们可以发现上述的两种方式都存在间断,那么要得到完整的轮廓我们就需要将他们结合在一起
我们使用addWeighted将他们相加,addWeigthed的用法可以翻一翻之前的文章
sobelxy = cv2.addWeighted(sobelx_1,0.5,sobely,0.5,0)
cv_show(sobelxy,'sobelxy')

直接计算
当dx和dy参数都为1时,将会进行Gx和Gy相结合的计算,但是效果一般不如单独计算再求和
sobelxy=cv2.Sobel(img,cv2.CV_64F,1,1,ksize=3)
sobelxy = cv2.convertScaleAbs(sobelxy)
cv_show(sobelxy,'sobelxy')

复杂图片的轮廓
我们依然用之前的kl.png来进行演示

img = cv2.imread('kl.png',cv2.IMREAD_GRAYSCALE)
sobelx = cv2.Sobel(img,cv2.CV_64F,1,0,ksize=3)
sobelx = cv2.convertScaleAbs(sobelx)
sobely = cv2.Sobel(img,cv2.CV_64F,0,1,ksize=3)
sobely = cv2.convertScaleAbs(sobely)
sobelxy = cv2.addWeighted(sobelx,0.5,sobely,0.5,0)
cv_show(sobelxy,'sobelxy')
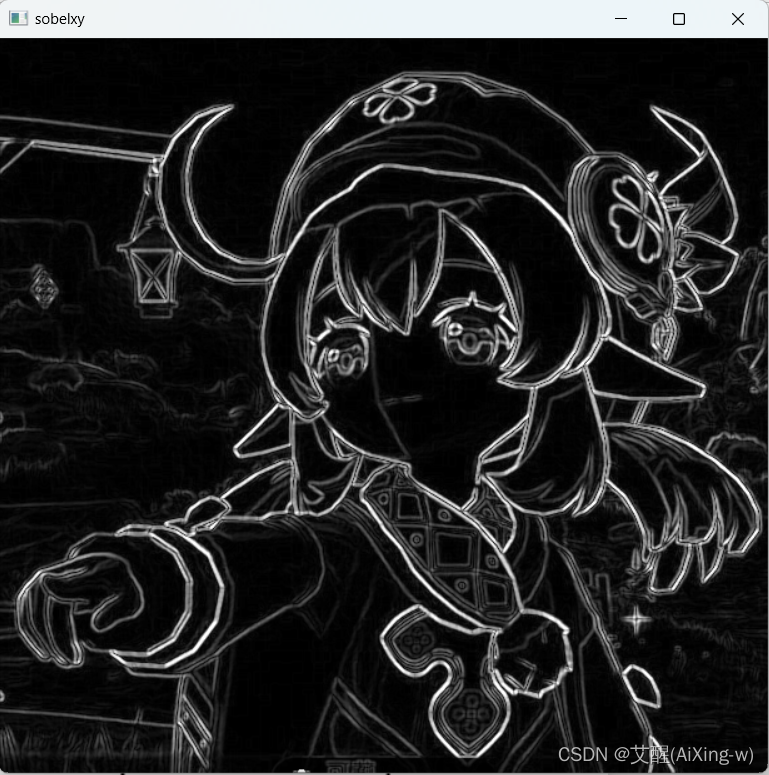
可以看到图像轮廓被完美的显示出来了
为了美观我们可以将图片反色
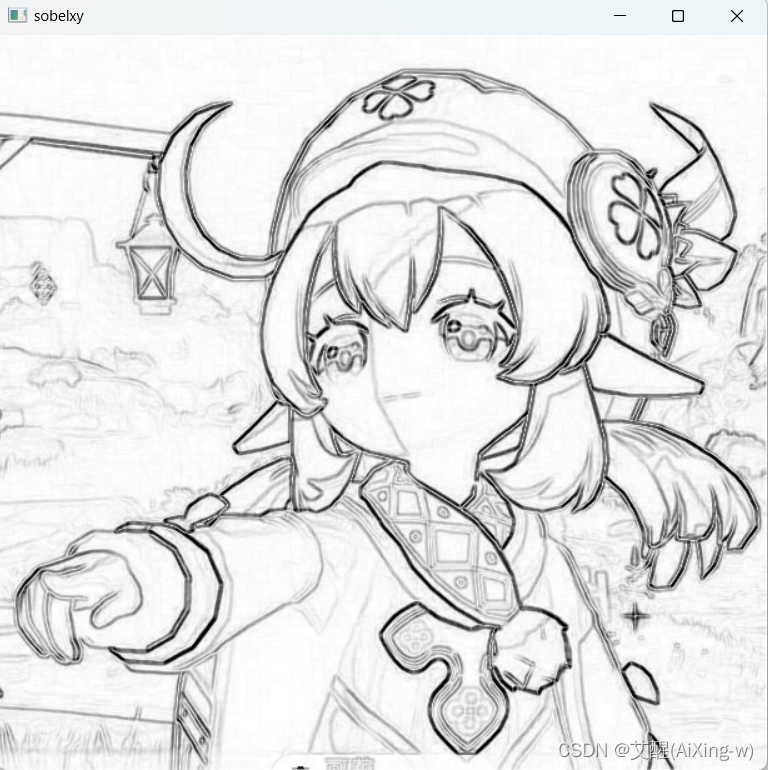
看到这个效果是不是跟之前文章中的边缘检测生成的线稿风格图像很像,事实上已经很接近了,我们将在后边的文章介绍边缘检测,本篇文章将继续介绍生成梯度的其他算子
Scharr算子与laplacian算子
scharr算子的定义
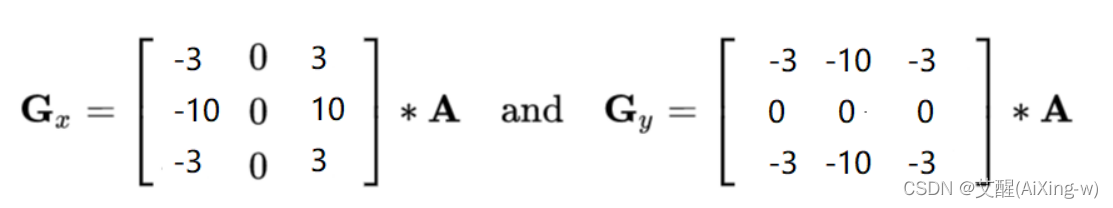
scharr算子和sobel算子基本思路是一样的,只不过他的值更大,呈现在图像中的效果就是对比更加明显,因为最终得到的值是sobel的倍数,而在opencv中,数越大就越白,对比度也就越高
laplacian算子定义
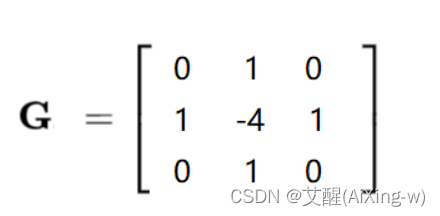
laplacian算子可以兼顾上下左右4个方向,但是因为上下左右四个方向的值都为1,这就导致得到的最终的数值将会比sobel算子得到的数值更小,所以对比度将会更低
三种算子的效果对比
为了方便观察我们依然在显示时进行反色处理,即255减去图像
img = cv2.imread('kl.png',cv2.IMREAD_GRAYSCALE)
sobelx = cv2.Sobel(img,cv2.CV_64F,1,0,ksize=3)
sobely = cv2.Sobel(img,cv2.CV_64F,0,1,ksize=3)
sobelx = cv2.convertScaleAbs(sobelx)
sobely = cv2.convertScaleAbs(sobely)
sobelxy = cv2.addWeighted(sobelx,0.5,sobely,0.5,0)
scharrx = cv2.Scharr(img,cv2.CV_64F,1,0)
scharry = cv2.Scharr(img,cv2.CV_64F,0,1)
scharrx = cv2.convertScaleAbs(scharrx)
scharry = cv2.convertScaleAbs(scharry)
scharrxy = cv2.addWeighted(scharrx,0.5,scharry,0.5,0)
laplacian = cv2.Laplacian(img,cv2.CV_64F)
laplacian = cv2.convertScaleAbs(laplacian)
res = np.hstack((sobelxy,scharrxy,laplacian))
cv_show(cv2.resize(255-res, (1600, 500)),'res')

结尾
有兴趣的话可以参照之前的文章:边缘检测生成(伪)手绘线稿风格的视频简易版教程
可以自己找一个视频运用本文中的方式生成(伪)线稿视频