算法设计与分析复习02：分而治之算法

复习重点

分而治之算法

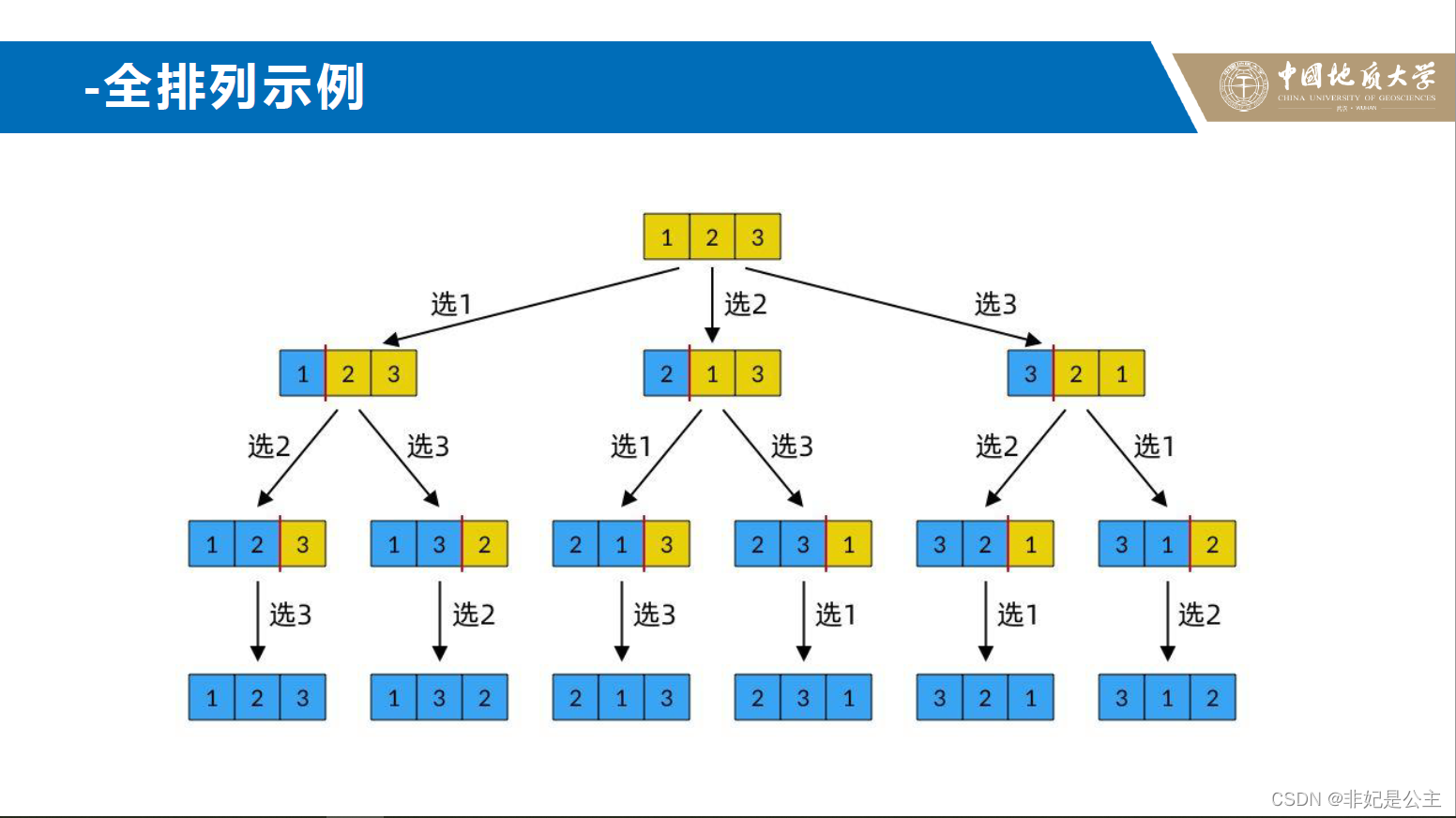
全排列递归算法

#include<vector>
#include<iostream>
using namespace std;
class Solution {
    vector<int> vis;
    void backtrace(vector<vector<int>>&res,vector<int>&nums,int first,int len, vector<int>& perm) {
        if (first == len) {
            res.push_back(perm);
        }
        else {
            for (int i = 0; i < len; i++) {
                if (vis[i])continue;
                perm.emplace_back(nums[i]);
                vis[i] = 1;
                backtrace(res, nums, first + 1, len, perm);
                vis[i] = 0;
                perm.pop_back();
            }
        }
    }
public:
    vector<vector<int>> permute(vector<int>& nums) {
        vector<vector<int>>res;
        vector<int> perm;
        vis.resize(nums.size());
        backtrace(res, nums, 0, nums.size(), perm);
        return res;
    }
};
int main() {
    Solution solution;
    vector<int> v = { 1,2,3 };
    vector<vector<int>> res = solution.permute(v);
    for (auto it = res.begin(); it != res.end(); it++) {
        for (auto it1 = it->begin(); it1 != it->end(); it1++) {
            cout << *it1 << " ";
        }
        cout << endl;
    }
    return 0;
}

矩阵乘法的Strassen算法

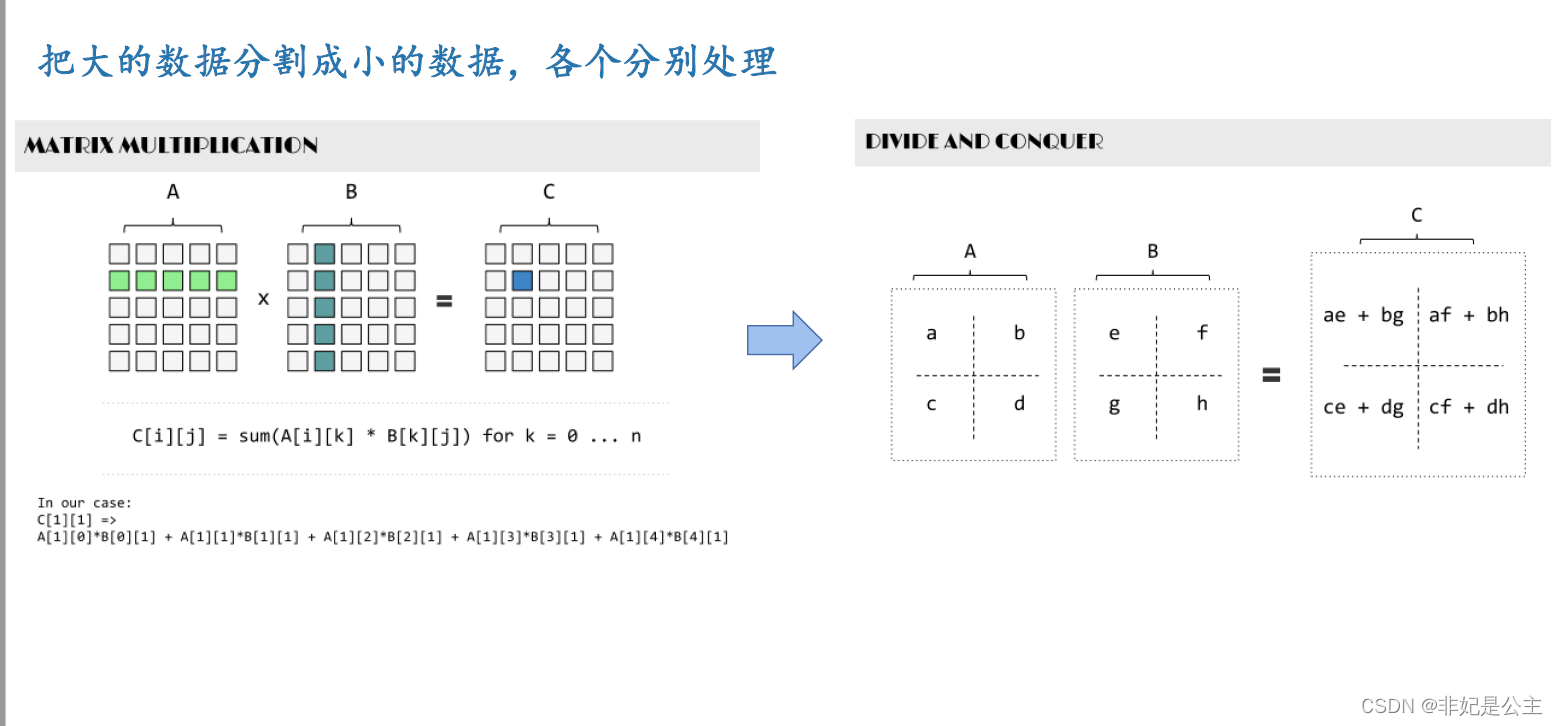
[Strassen算法步骤](详解矩阵乘法中的Strassen算法 - 知乎 (zhihu.com))

算法分析：
$$T(n)=\{\begin{array}{cc}O(1)& \text{n=1}\\ 7T(\frac{n}{2})+O(n^2)& \text{n>1}\end{array}$$
主方法求得算法复杂度为：
$$n^{lo{g}_{2}7}$$

棋盘覆盖

棋盘覆盖问题看下面这张图，由于要求期盼规模为
$$2^k\times 2^k$$
有一定的局限性，但是是理解递归与分治的好问题，只看下面这张图：

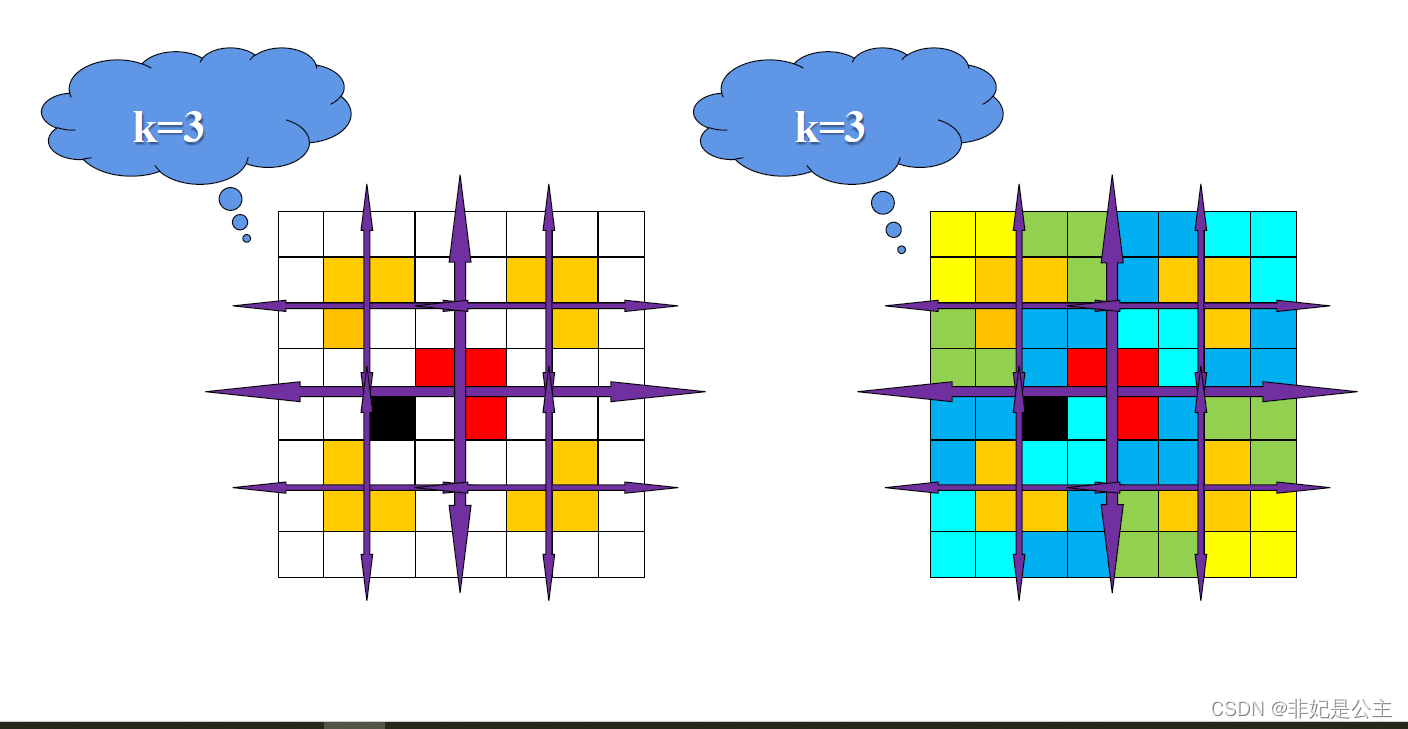
每一个块对称选择。

线性时间选择

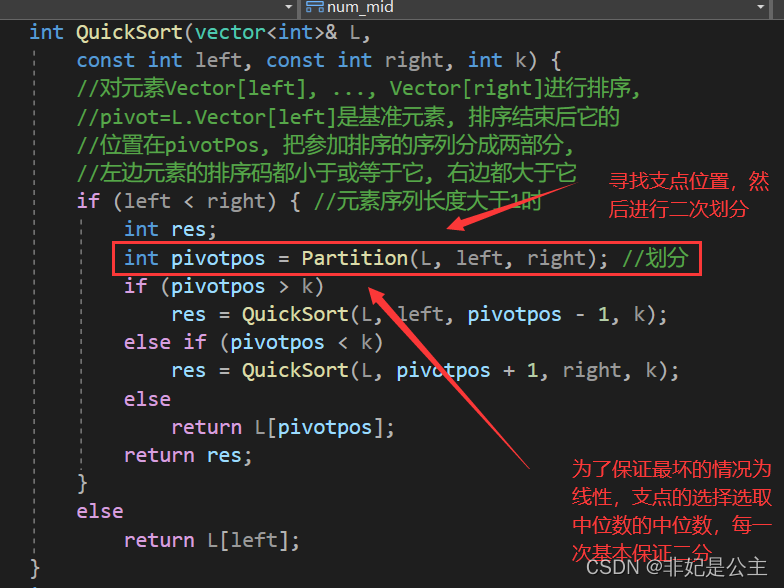
主要思想：利用快排，进行部分排序，不断缩小范围。
核心代码：

全部代码：

#include<vector>
#include<iostream>
#include<algorithm>
#include<queue>

using namespace std;

class Solution {
    struct num_mid {
        int pos;
        int num;
        bool operator<(const num_mid nm) {
            return this->num < nm.num;
        }
        num_mid(int p, int n) :pos(p), num(n) {}
    };
    int Partition(vector<int>& Vector, const int low, const int high) {
        //数据表类的共有函数
        int pivotpos;
        int pivot; //基准元素
        if (high - low > 5) {
            vector<num_mid>tmp;
            for (int i = low; i <= high - 4; i += 5) {
                sort(Vector.begin() + i, Vector.begin() + i + 4);
                tmp.push_back(num_mid(i + 2, Vector[i + 2]));
            }
            sort(tmp.begin(), tmp.end());
            pivotpos = low;
            pivot = Vector[tmp[tmp.size() / 2].pos];
            swap(Vector[low], Vector[tmp[tmp.size() / 2].pos]);
        }
        else {
            sort(Vector.begin() + low, Vector.begin() + high);
            pivotpos = low;
            pivot = Vector[(low + high) / 2]; //基准元素
            swap(Vector[low], Vector[(low + high) / 2]);
        }
        for (int i = low + 1; i <= high; i++)
            //检测整个序列, 进行划分
            if (Vector[i] < pivot) {
                pivotpos++;
                if (pivotpos != i)
                    swap(Vector[pivotpos], Vector[i]);
            } //小于基准的交换到左侧去
        Vector[low] = Vector[pivotpos];
        Vector[pivotpos] = pivot;
        //将基准元素就位
        return pivotpos; //返回基准元素位置
    }

    int QuickSort(vector<int>& L,
        const int left, const int right, int k) {
        //对元素Vector[left], ..., Vector[right]进行排序, 
        //pivot=L.Vector[left]是基准元素, 排序结束后它的
        //位置在pivotPos, 把参加排序的序列分成两部分,
        //左边元素的排序码都小于或等于它, 右边都大于它
        if (left < right) { //元素序列长度大于1时
            int res;
            int pivotpos = Partition(L, left, right); //划分
            if (pivotpos > k)
                res = QuickSort(L, left, pivotpos - 1, k);
            else if (pivotpos < k)
                res = QuickSort(L, pivotpos + 1, right, k);
            else
                return L[pivotpos];
            return res;
        }
        else
            return L[left];
    }
public:
    int findKthLargest(vector<int>& nums, int k) {
        int res = QuickSort(nums, 0, nums.size() - 1, nums.size() - k);
        return res;
    }
};

int main() {
    vector<int> v = { 3,2,3,1,2,4,5,5,6 };
    int res = QuickSort(v, 0, v.size() - 1, v.size() - 4);
    cout << res;    
}

时间复杂度分析：假设，基本实现二分，线性选择支点的时间复杂度为$O(n)$，递归的时间复杂度如下：
$$T(n)=T(\frac{n}{2})+O(n)$$
依据主定理，时间复杂度为$O(n)$。