微❤关注“电气仔推送”获得资料(专享优惠)
参考文献:

主要内容:
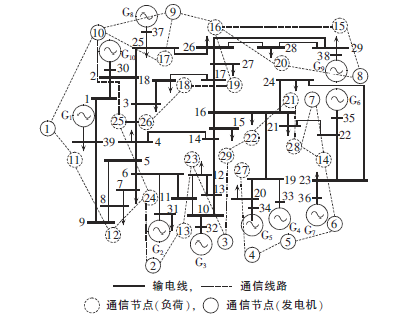
应用多智能体系统中的一致性算法,以发电机组的增量成本和柔性负荷的增量效益作为一致性变量,设计一种用于电力系统经济调度的算法,通过分布式优化的方式求解经济调度问题。
程序完全采用论文中的数据,对论文中的4种场景进行了复现。
场景1 验证了该分布式调度算法与集中式调度算法一样,能收敛到最优解;
场景2 验证了该分布式调度策略对不同通信拓扑的适应性;
场景3 验证了该分布式调度策略能够有效应对电力元件功率约束发生作用的情形;
场景4 验证了该分布式调度策略能够使电力元件具备“即插即用”的能力。
部分程序:
%迭代%
l=[li lj];
ll=zeros(801,29);
ll(1,:)=l;
dp=zeros(1,801);
dp(1)=spd(1)-spg(1);
pgg=zeros(801,10);
pgg(1,:)=pg;
pdd=zeros(801,19);
pdd(1,:)=pd;
for t=1:1:800
for n=1:1:29 %更新lambda的值
if n==1
ll(t+1,n)=sum(a(n,:).*ll(t,:))+0.005*dp(t);
elseif n==11
ll(t+1,n)=sum(a(n,:).*ll(t,:))+0.005*dp(t);
else
ll(t+1,n)=sum(a(n,:).*ll(t,:));
end
end
for i=1:1:10 %判断pg是否越限并赋值
if (ll(t,i)-be(i))/(2*ga(i))>=pgmax(i)
pgg(t+1,i)=pgmax(i);
elseif (ll(t,i)-be(i))/(2*ga(i))<=pgmin(i)
pgg(t+1,i)=pgmin(i);
else
pgg(t+1,i)=(ll(t,i)-be(i))/(2*ga(i));
end
end
for j=1:1:19 %判断pd是否越限并赋值
if (ll(t,j+10)-b(j))/(2*c(j))>=pdmax(j)
pdd(t+1,j)=pdmax(j);
elseif (ll(t,j+10)-b(j))/(2*c(j))<=pdmin(j)
pdd(t+1,j)=pdmin(j);
else
pdd(t+1,j)=(ll(t,j+10)-b(j))/(2*c(j));
end
end
spg(t+1)=sum(pdd(t+1,:));
spd(t+1)=sum(pgg(t+1,:));
dp(t+1)=sum(pdd(t+1,:))-sum(pgg(t+1,:));
end
输出结果
场景一
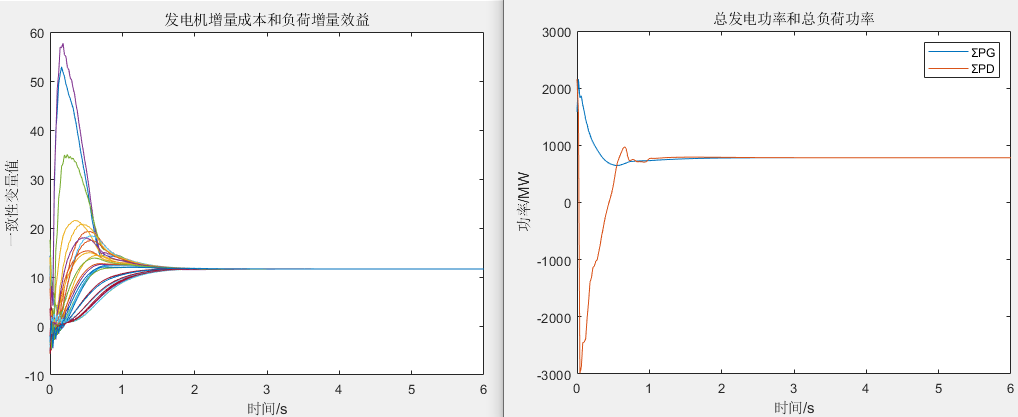
场景二
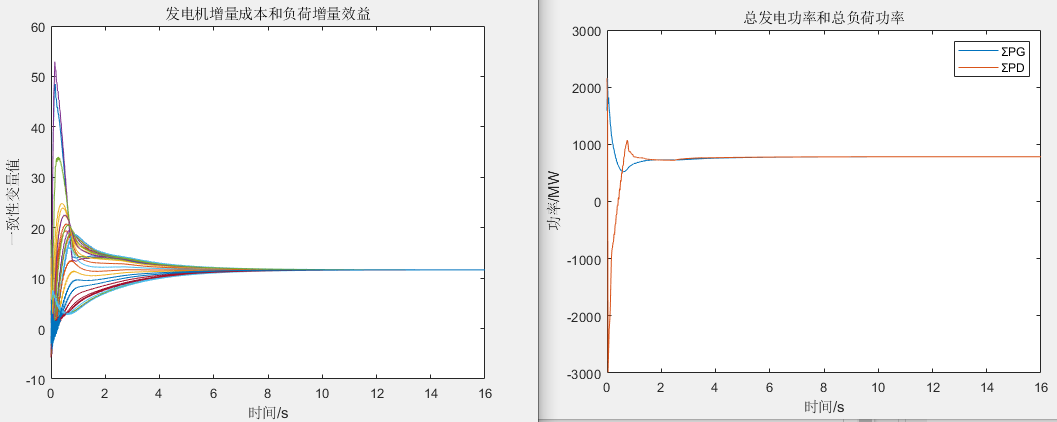
场景三
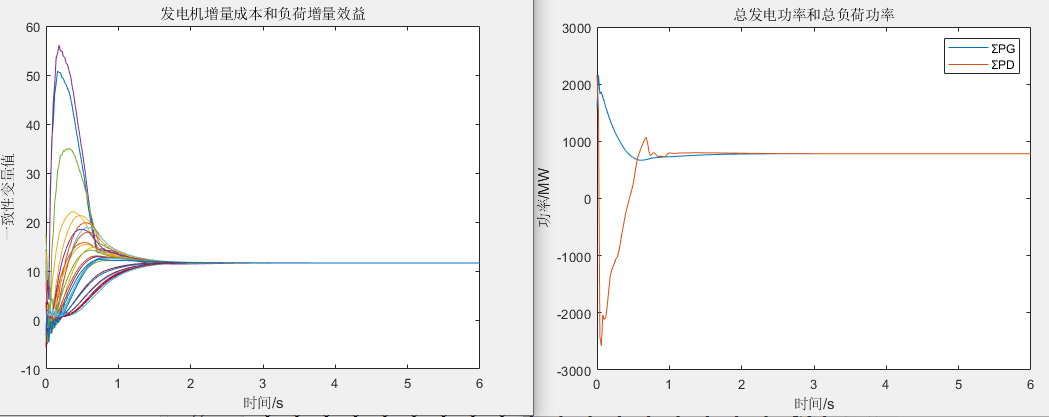
场景四

结论:
未来电网中柔性负荷大量渗透,用户不再仅仅是电网末端的刚性负荷,而是能够参与系统运行、实现与电源互动的柔性负荷。相比于集中式优化调度,在实现柔性负荷“即插即用”、降低通信网投资、应对通信网拓扑结构多变等方面,分布式优化调度在未来电网经济调度中具有一定的应用前景。



![neuq-acm预备队训练week 10 P1129 [ZJOI2007] 矩阵游戏](https://img-blog.csdnimg.cn/direct/eca6afc54d5a4b9ab62f51666c074d88.png)