代码:
import java.util.Scanner;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
// 注意 hasNext 和 hasNextLine 的区别
while (in.hasNextInt()) { // 注意 while 处理多个 case
int n=in.nextInt();
int m=in.nextInt();
int q=in.nextInt();
//因为题目中的矩阵下标从 1 开始,而我们创建的数组下标从 0 开始,所以需要留一行
int[][]arr=new int[n+1][m+1];
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
arr[i][j]=in.nextInt();
}
}
//获取前缀和数组 dp
//记录的是区间数据的总和,很容易溢出,所以用 long 类型
long[][]dp=new long[n+1][m+1];
//填充 dp 数组
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
dp[i][j]=dp[i][j-1]+dp[i-1][j]-dp[i-1][j-1]+arr[i][j];
}
}
//循环查询 q 次
while(q>0){
int x1=in.nextInt();
int y1=in.nextInt();
int x2=in.nextInt();
int y2=in.nextInt();
//使用 dp 数组
System.out.println(dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1]);
q--;
}
}
}
}题解:
题目要求我们获取(x1,y1)~(x2,y2)这个区间内的数据总和,这是一个典型的前缀和问题,如果我们使用暴力解法,我们就需要遍历数组中这个区间的所有数据,查询 q 次我们就需要遍历 q 次,所以时间复杂度会为 O(n*m*q),在该题用暴力解法肯定时间会过长的
所以我们需要使用前缀和解法,我们可以定义一个前缀和数组 dp ,dp[ i ][ j ] 就代表从(1,1)~ (i,j)这个区间内的数据总和,因为我们要统计从(1,1)到各个位置区间的数据总和,所以 dp 数组的大小和二维数组 arr 的大小相同
现在我们先先考虑如何填充 dp 数组,然后再考虑如何使用 dp 数组获得结果,dp 数组一般第 0 行和 第 0 列 的数据是手动初始化的,而不是程序填充的,为了避免越界问题(后面说明),所以对于示例 1 来说我们还没填充的 dp 数组如下所示
0 1 2 3 4 5
0 0 0 0 0 0 0
1 0
2 0
3 0
因为题目给出的数组下标是从 1 开始的,所以下标带 0 的位置是不存在的,所以前缀和都设为 0 ,这也代表我们在填充 dp[ i ][ j ] 时就已经知道了 dp[ i-1 ][ j-1 ],dp[ i ][ j-1 ],dp[ i-1 ][ j ] 的值,我们如何计算 dp[ i ][ j ] 的值呢?为了方便理解我画了下面的图
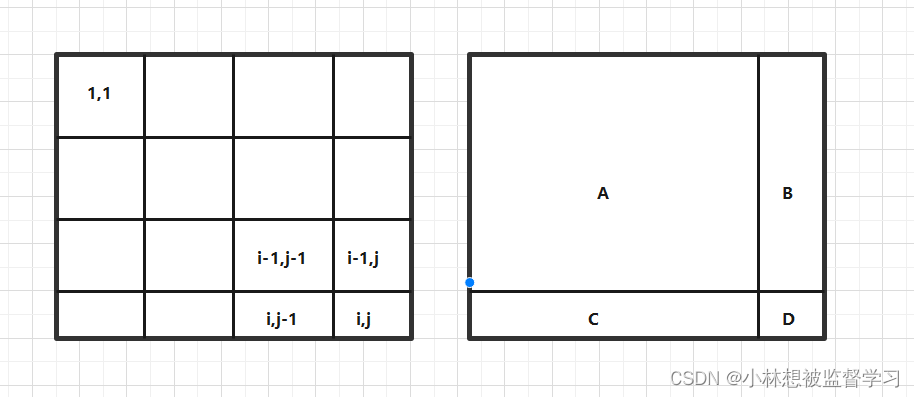
我们想要计算 dp[ i ][ j ] ,即从(1,1)~ (i,j)这个区间内的数据总和,根据右边的图,我们要计算的就是 A+B+C+D 的面积,我们可以将该式子替换为 (A+C)+(A+B)-A+D,A+C 的面积就是 dp[ i ][ j-1 ] 的值,A+B 的面积就是 dp[ i-1 ][ j ] 的值,A 的面积就是 dp[ i-1 ][ j-1 ] 的值,D 的面积就是 arr[ i ][ j ] 的值
所以我们可以得出式子 dp[ i ][ j ] = dp[ i ][ j-1 ] + dp[ i-1 ][ j ] - dp[ i-1 ][ j-1 ] + arr[ i ][ j ],填充 dp 数组的顺序是先 从左到右 再 从上到下 ,根据该式子,当 i=0 或 j=0 时就会有 -1 的下标,就存在越界问题
现在得出了 dp 数组的填充式子,我们再研究如何通过 dp 数组得到结果便解出该题,为了方便理解,我画了下面的图
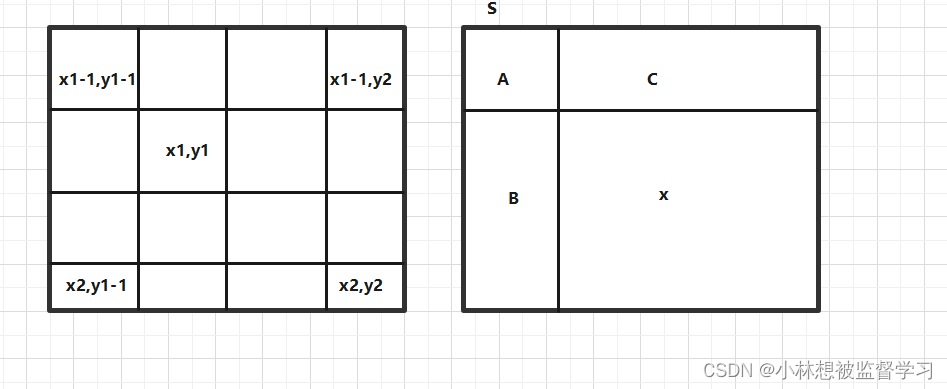
如上图,我们想要获取(x1,y1)~(x2,y2)这个区间内的数据总和 x ,相当于要计算
s - A - B - C 的值,我们将该表达式修改为 s - (A+B) - (A+C) + A ,s 的面就是 dp[ x2 ][ y2 ], A+B 的面积就是 dp[ x2 ][ y1-1 ],A+C 的面积就是 dp[ x1-1 ][ y2 ], A 的面积就是 dp[ x1-1 ][ y1-1 ] ,所以我们得出(x1,y1)~(x2,y2)这个区间内的数据总和 x = dp[ x2 ][ y2 ] - dp[ x2 ][ y1-1 ] - dp[ x1-1 ][ y2 ] + dp[ x1-1 ][ y1-1 ]
上面的两个表达式就是本题的核心了