小分互换

$$\begin{gathered} \frac{1}{2}=50\%\frac{1}{3}=33.3\%\frac{1}{4}=25\%\frac{1}{5}=20\%\frac{1}{6}=16.7\% \\ \frac{1}{7}=14.3\%\frac{1}{8}=12.5\%\frac{1}{9}=11.1\%\frac{1}{10}=10\%\frac{1}{11}=9.1\% \\ \frac{1}{12}=8.3\%\frac{1}{13}=7.7\%\frac{1}{14}=7.1\%\frac{1}{15}=6.7\% \end{gathered}$$

基本公式

增长量：x，增长率：R，现期：B，基期：A
$$\begin{gathered} 增长量x=现期B-基期A=现期B-\frac{现期B}{1+增长率R}=\frac{增长率R}{1+增长率R}\ast 现期B \\ 增长率R=\frac{增长量x}{基期A}=\frac{现期B-基期A}{基期A} \\ 现期B=基期A\ast (1+增长率R) \\ 基期A=\frac{现期B}{1+增长率R} \end{gathered}$$

比重

整体占部分的比例：部分 / 整体

倍数、比值

倍数：A是B的多少倍，A / B

比值：A与B的比值，A:B即A / B

平均数

后 / 前

示例：

人均GDP：GDP / 人数

每万元GDP的能耗： 能耗 / GDP

同比与环比

同比：与上年同期比，如2015年5月和2014年5月

环比：与上个统计周期比，如2020年5月与2020年4月

百分数与百分比

百分数：结尾%

百分比：百分数加减的运算单位（多少个百分点)，例：高20个百分点

成数与翻番

成数：一成相当于10%

翻番：翻一番相当于原来的2倍

顺差与逆差

顺差：出口额 > 进口额

逆差：进口额 > 出口额

速算技巧

直除法

适用类型：A / B

1. 观察选项：首位，首位相同时看第二位
2. 截位：根据第一步的结果，四舍五入取前两位或三位
3. 做除法：列式，要几位就算几位

加减法

对齐后从高位计算

特殊分数化简

适用类型：
$$x=\frac{B}{1+R}\ast R$$
其中的R可以化简为特殊分数。

示例：
$$x=\frac{23576}{1+7.121\%}\ast 7.121\%根据小分互换，7.1\%=\frac{1}{14},因此式子可以化简(近似)为x=\frac{23576}{1+\frac{1}{14}}\ast \frac{1}{14},化简得x=\frac{23576}{15},这样就可以减少计算了。$$

化除为乘近似计算

$$\frac{A}{1-a\%}\approx A\ast (1+a\%)\boxed{a\%\le 5\%}$$

隔年增长率

2022年相对于2021年的增长率是a%，2023年相对于2022年的增长率是b%，求2023年相对于2021年的增长率是多少？

画图：

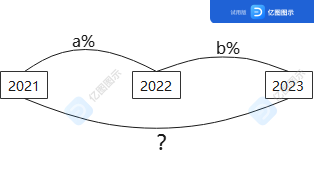
解题：
$$\begin{gathered} x=a\%+b\%+a\%\ast b\% \\ 注意：增长率正负都可以，两个增长率的乘积小于10\%，即\mid a\%\mid \mid b\%\mid \le 10\% \end{gathered}$$

合成增长率

适用类型：

两部分合成整体，示例： 进口额 + 出口额 = 进出口额等。

合成增长率 x 介于两部分增长率之间，偏向于基数(多指现期)较大的一方。

示例：

2017年，进口额3000元，同比增长率为10%，出口额6000元，同比增长率20%，求进出口总额的增长率？

A：9.5% B：14.5% C：16.5% D：17.5%

解析：

十字交叉法，当无法一次性看出的时候，可以使用该方法。

上面该题，通过合成增长率介于两部分增长率之间，偏向基数较大的一方，只能排除两个选项，因此需要使用十字交叉法。

如下：

高频考点

第一节 增长率R常考题型

基本公式：
$$R=\frac{x}{A}=\frac{B-A}{A}$$
考点识别：

增长/减少 + %

常考题型：

• 增长率计算
• 增长率判断
• 增长率大小比较

第二节 基期量A常考题型

基本公式：
$$A=\frac{B}{1+R}$$
考点识别：

已知B(现在)，求A(过去)

常考题型：

• 一般基期量A
• 隔年基期量，先求隔年增长率
• 基期量做差，先算现期差排除选项，后分别求出基期后计算
• 基期量大小比较

第三节 增长量x常考题型

基本公式：
$$x=B-A=B\ast \frac{R}{1+R}$$
考点识别：

增长/减少 + 多少 + 单位    或者  直接求xx的增长量x

常考题型：

• 增长量计算

• 增长量大小比较

  口诀：大大则大，一大一小看倍数（大大则大，指的是现期B和增长率R）
  一大一小看倍数详解：
  示例：
  城市1的现期是1500，增长率是25%，而城市2的现期是3000，增长率是20%，则城市1和城市2的增长量x谁更大。
  解析：
  城市1 1500 25%
  城市2 3000 20%
  则城市2的现期是城市1的2倍，而城市1的增长率是城市2的1.25倍，2 > 1.25，因此城市2的增长量x更大。
  

注：当R大的时候，

第四节 比重相关常考题型

现期B比重

考点识别：

C部分占D整体的比重

基期A比重

公式：
$$比重=\frac{A}{B}\ast \frac{1+b\%}{1+a\%}\approx \frac{A}{B}\ast (1+b\%-a\%)其中，A、B为现期，a\%、b\%为增长率$$

比重变化

比重变化方向：

1. 口诀： 部分增长率 > 整体增长率，则比重上升，否则下降。

2. 比重变化 < | a% - b%|

3. 具体计算：
   $$比重变化=\frac{A}{B}\ast \frac{a\%-b\%}{1+a\%}$$

第五节 平均数与倍数常考题型

平均数

平均、均、每、单位

列式形式：后 / 前

平均数增长率

考点识别：

平均(A/B) + 增长/减少 + %

公式：
$$平均数增长率=\frac{a\%-b\%}{1+b\%}$$

倍数

A是B的多少倍

列式形式：A / B

隔年倍数 = 1+ 隔年增长率

保持增长率不变：
$$B=A(1+R{)}^{n}n表示n年$$
保持增量不变：
$$B=A+n\ast x$$