1. 重建二叉树

原题链接：

剑指 Offer 07. 重建二叉树 - 力扣（LeetCode）https://leetcode.cn/problems/zhong-jian-er-cha-shu-lcof/submissions/

1.1 题目描述

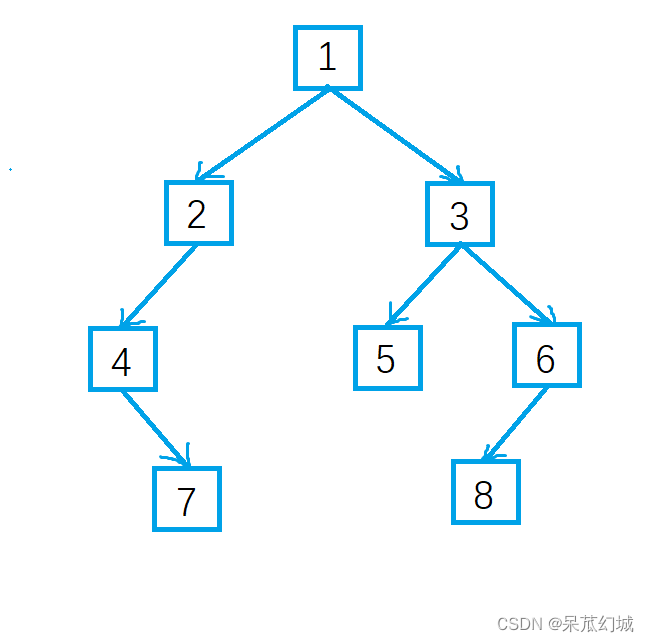
输入某二叉树的前序遍历和中序遍历的结果，请重建该二叉树。假设输入的前序遍历和中序遍历结果中不含有重复的数字。例如，输入前序遍历序列｛1,2,4,7,3,5,6,8｝和中序遍历序列｛4,7,2,1,5,3,8,6｝要求你重建如下图所示的二叉树并返回它的根结点。

如图所示：根结点为1。

1.2 复习基础知识

前序遍历就是在遍历二叉树时先访问根结点再访问左子树，最后访问右子树。

中序遍历就是在遍历二叉树时先访问左子树，再访问根结点，最后访问右子树。

后序遍历就是在遍历二叉树时先访问左子树，再访问右子树，最后访问根结点。
下面以一颗满二叉树为例，简单复习一下前中后序的遍历：

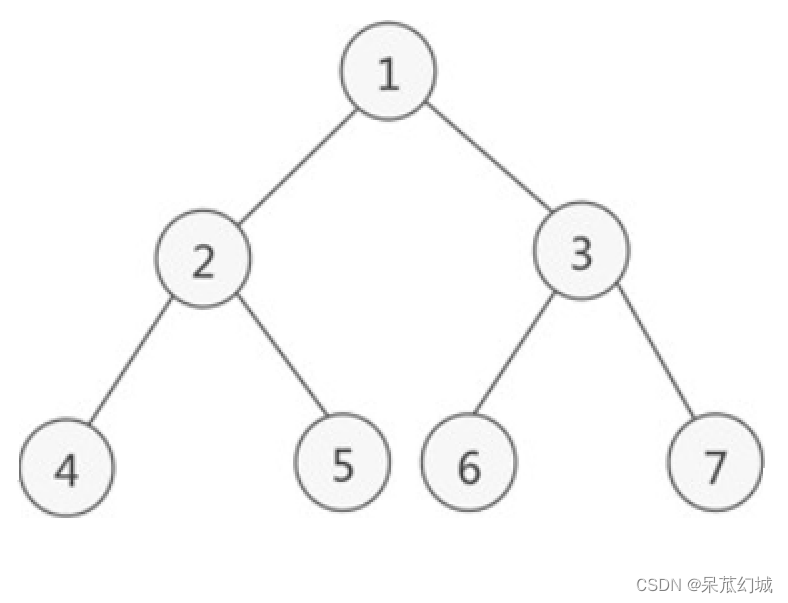
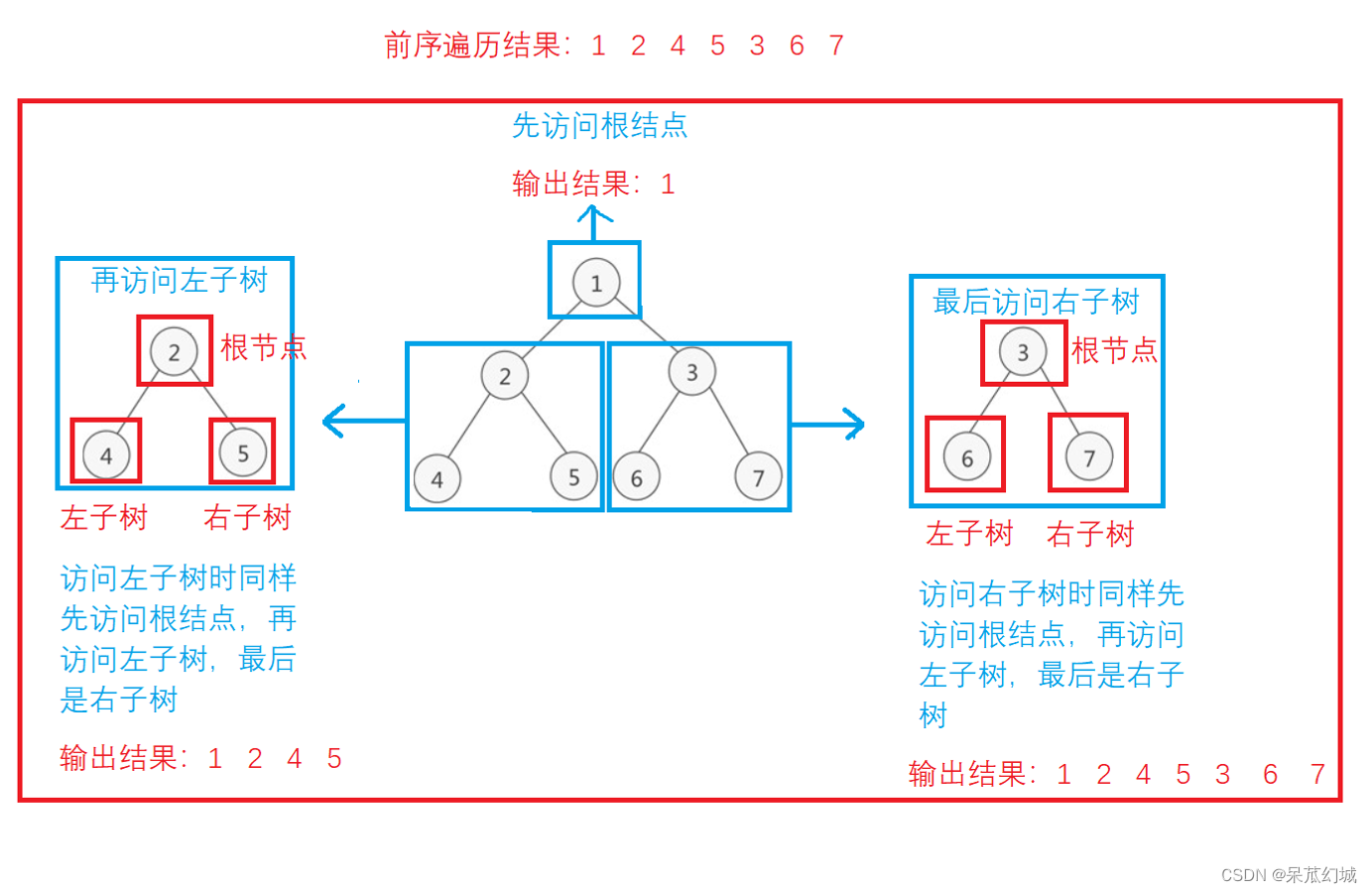
同理可得到中序遍历结果： 4 2 5 1 6 3 7。

后序遍历结果：4 5 2 6 7 3 1。

//前序遍历
void PrevOrder(BTNode* root)
{
	//递归结束条件
	if (root == NULL)
	{
		return;
	}
		
	printf("%c ", root->data);

	//左子树
	PrevOrder(root->left);
	//右子树
	PrevOrder(root->right);
}

//中序遍历
void InOrder(BTNode* root)
{
	//递归结束条件
	if (root == NULL)
	{
		return;
	}

	//左子树
	InOrder(root->left);

	printf("%c ", root->data);

	//右子树
	InOrder(root->right);
}

//后序遍历
void PostOrder(BTNode* root)
{
	//递归结束条件
	if (root == NULL)
	{
		return;
	}

	//左子树
	PostOrder(root->left);

	//右子树
	PostOrder(root->right);

    printf("%c ", root->data);
}

1.3 思路分析

有了上面的基础知识，就能够解决这道题目啦！

还是以这组例子分析哈：

输入前序遍历序列｛1,2,4,7,3,5,6,8｝和中序遍历序列｛4,7,2,1,5,3,8,6｝。

如下图所示，前序遍历的第一个数字1就是根结点的值。扫描中序遍历的序列就能确定根结点值的位置。根据中序遍历的特点，在根结点的值1前面的3个数字都是左子树节点的值，位于1后面的数字都是右子树的值。

由于在中序遍历中，有3个数字是左子树节点的值，因此左子树共有3个左子节点。同样，在前序遍历序列中，根结点后面的3个数字就是3个左子树节点的值，再后面的所有数字都是右子树节点的值。这样我们就在前序遍历和中序遍历两个序列中分别找到了左，右子树对应的子序列。

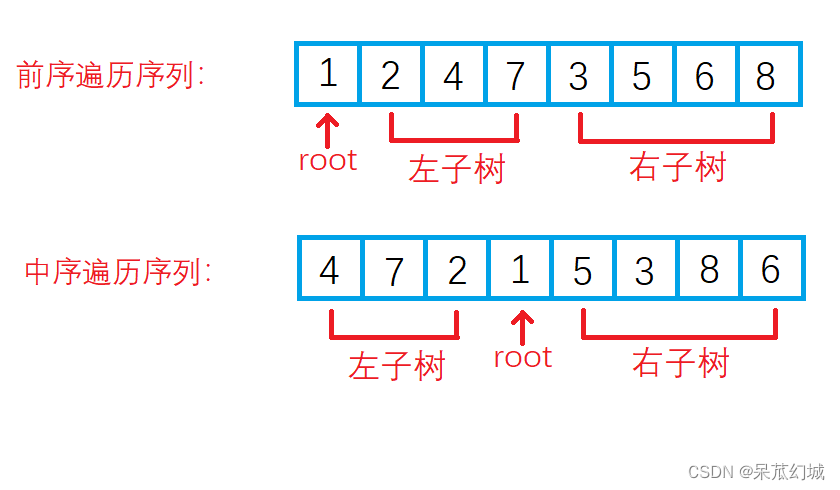
现在我们搞清楚了如何在前序遍历和中序遍历序列中找到根结点左子树，右子树！完成这一步我们就构建出了一个根结点，我们可以用同样的方法分别构建左，右子树。也就是说，接下来的事情就可以交给递归去做！！

如何递归呢？

我们把前序遍历的左子树拿出来，当成一个新的前序遍历序列，把中序遍历的左子树拿出来当成一个新的中序遍历序列，再去找到新的前序遍历序列和新的中序遍历中的根结点，左子树，右子树。以此类推，右子树同理。

右子树同理哈！！！！！

//递归重建二叉树，因为两个序列的大小是一样的，所以传一个size即可
struct TreeNode* recurison(int* arr1, int* arr2, int size)
{
    //开辟空间，构建节点
    struct TreeNode* root = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    //记录前序遍历序列中下标为0的值，即根结点的值
    int val = arr1[0];
    //赋值，创建结点
    root->val = val;
    //遍历中序序列找到根结点的下标
    int i=0;
    for(i=0; i < size;i++)
    {
        if(val == arr2[i])
        {
            break;
        }
    }

    if(i != 0) //如果下标在中序序列中不为0，取左子树出来，递归构建左子树
    {
        root->left = recurison(arr1 + 1, arr2, i);
    }

    else //如果下标在中序序列中为0，左子树不存在，令root->left = NULL
    {
        root->left = NULL;
    }

    if(i != size -1) //如果下标在中序序列中不为size - 1，取右子树出来，递归构建右子树
    {
        root->right = recurison(arr1 + 1 + i, arr2 + i + 1, size - i - 1);
    }
    else //如果下标在中序序列中为size - 1，右子树不存在，令root->right = NULL
    {
        root->right = NULL;
    }
    //返回当前层的根结点，连接双亲节点
    return root;
}

struct TreeNode* buildTree(int* preorder, int preorderSize, int* inorder, int inorderSize){
    if(preorderSize==0 || inorderSize==0) //处理输入为空的情况
    {
        return NULL;
    }
    return recurison(preorder, inorder, inorderSize);
}