1.最短路径定义及性质
有了加权有向图之后,我们立刻就能联想到实际生活中的使用场景,例如在一副地图中,找到顶点a与地点b之间的路径,这条路径可以是距离最短,也可以是时间最短,也可以是费用最小等,如果我们把 距离/时间/费用看做是成本,那么就需要找到地点a和地点b之间成本最小的路径,也就是我们接下来要解决的最短路径问题。
定义:
在一副加权有向图中,从顶点s到顶点t的最短路径是所有从顶点s到顶点t的路径中总权重最小的那条路径
性质:
1.路径具有方向性;
2.权重不一定等价于距离。权重可以是距离、时间、花费等内容,权重最小指的是成本最低
3.只考虑连通图。一副图中并不是所有的顶点都是可达的,如果s和t不可达,那么它们之间也就不存在最短路径,为了简化问题,这里只考虑连通图。
4.最短路径不一定是唯一的。从一个顶点到达另外一个顶点的权重最小的路径可能会有很多条,这里只需要找出一条即可。
最短路径树:
给定一副加权有向图和一个顶点s,以s为起点的一棵最短路径树是图的一副子图,它包含顶点s以及从s可达的所有顶点。这棵有向树的根结点为s,树的每条路径都是有向图中的一条最短路径。
2.最短路径树API设计
计算最短路径树的经典算法是dijstra算法
| 类名 | DijkstraSP |
|---|---|
| 构造方法 | public DijkstraSP(EdgeWeightedDigraph G, int s):根据一副加权有向图G和顶点s,创建一个计算顶点为s的最短路径树对象 |
| 成员方法 | 1.private void relax(EdgeWeightedDigraph G, int v):松弛图G中的顶点v 2.public double distTo(int v):获取从顶点s到顶点v的最短路径的总权重 3.public boolean hasPathTo(int v):判断从顶点s到顶点v是否可达 4.public Queue pathTo(int v):查询从起点s到顶点v的最短路径中所有的边 |
| 成员变量 | 1.private DirectedEdge[] edgeTo: 索引代表顶点,值表示从顶点s到当前顶点的最短路径上的最后一条边 2.private double[] distTo: 索引代表顶点,值从顶点s到当前顶点的最短路径的总权重 3.private IndexMinPriorityQueue pq:存放树中顶点与非树中顶点之间的有效横切边 |
3.松弛技术
松弛这个词来源于生活:一条橡皮筋沿着两个顶点的某条路径紧紧展开,如果这两个顶点之间的路径不止一条,还有存在更短的路径,那么把皮筋转移到更短的路径上,皮筋就可以放松了。松弛这种简单的原理刚好可以用来计算最短路径树。
在我们的API中,需要用到两个成员变量edgeTo和distTo,分别存储边和权重。一开始给定一幅图G和顶点s,我们只知道图的边以及这些边的权重,其他的一无所知,此时初始化顶点s到顶点s的最短路径的总权重disto[s]=0;顶点s到其他顶点的总权重默认为无穷大,随着算法的执行,不断的使用松弛技术处理图的边和顶点,并按一定的条件更新edgeTo和distTo中的数据,最终就可以得到最短路劲树。
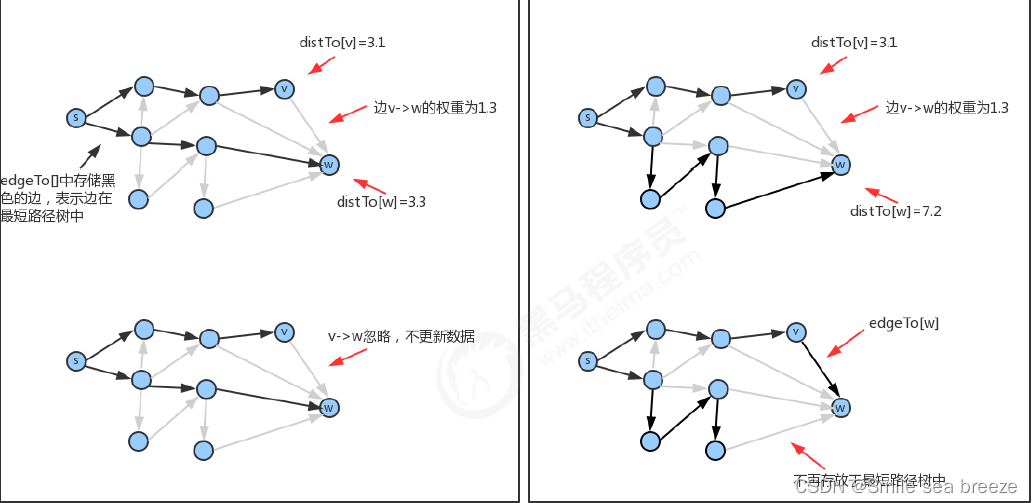
边的松弛:
放松边v->w意味着检查从s到w的最短路径是否先从s到v,然后再从v到w?
如果是,则v-w这条边需要加入到最短路径树中,更新edgeTo和distTo中的内容:edgeTo[w]=表示v->w这条边的
DirectedEdge对象,distTo[w]=distTo[v]+v->w这条边的权重;
如果不是,则忽略v->w这条边。
顶点的松弛:
顶点的松弛是基于边的松弛完成的,只需要把某个顶点指出的所有边松弛,那么该顶点就松弛完毕。例如要松弛顶
点v,只需要遍历v的邻接表,把每一条边都松弛,那么顶点v就松弛了。
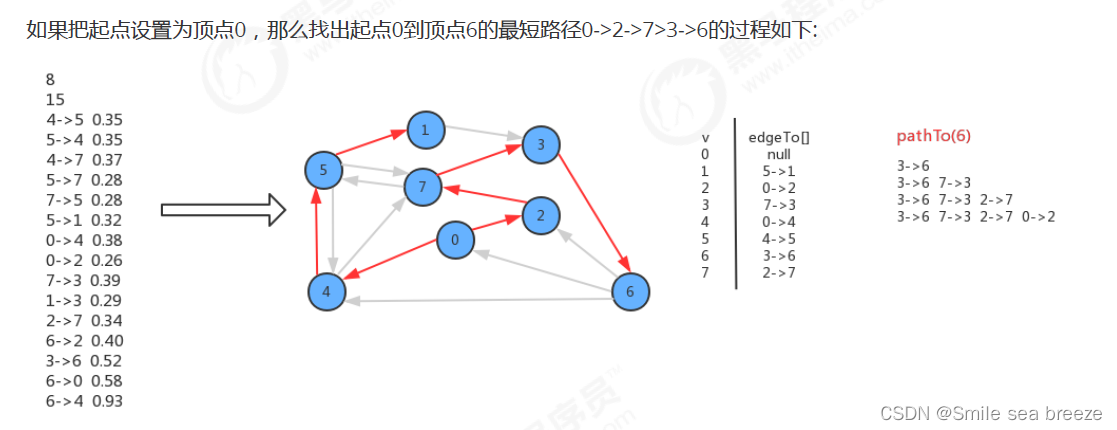
4.Dijstra算法实现
Disjstra算法的实现和Prim算法很类似,构造最短路径树的每一步都是向这棵树中添加一条新的边,而这条新的边是有效横切边pq队列中的权重最小的边。
public class DijkstraSP {
//索引代表顶点,值表示从顶点s到当前顶点的最短路径上的最后一条边
private DirectedEdge[] edgeTo;
//索引代表顶点,值从顶点s到当前顶点的最短路径的总权重
private double[] distTo;
//存放树中顶点与非树中顶点之间的有效横切边
private IndexMinPriorityQueue<Double> pq;
//根据一副加权有向图G和顶点s,创建一个计算顶点为s的最短路径树对象
public DijkstraSP(EdgeWeightedDigraph G, int s){
//创建一个和图的顶点数一样大小的DirectedEdge数组,表示边
this.edgeTo = new DirectedEdge[G.V()];
//创建一个和图的顶点数一样大小的double数组,表示权重,并且初始化数组中的内容为无穷大,无穷
大即表示不存在这样的边
this.distTo = new double[G.V()];
for (int i = 0; i < distTo.length; i++) {
distTo[i] = Double.POSITIVE_INFINITY;
}
//创建一个和图的顶点数一样大小的索引优先队列,存储有效横切边
this.pq = new IndexMinPriorityQueue<>(G.V());
//默认让顶点s进入树中,但s顶点目前没有与树中其他的顶点相连接,因此初始化distTo[s]=0.0
distTo[s] = 0.0;
//使用顶点s和权重0.0初始化pq
pq.insert(s, 0.0);
//遍历有效边队列
while (!pq.isEmpty()) {
//松弛图G中的顶点
relax(G, pq.delMin());
}
}
//松弛图G中的顶点v
private void relax(EdgeWeightedDigraph G, int v){
//松弛顶点v就是松弛顶点v邻接表中的每一条边,遍历邻接表
for (DirectedEdge e : G.adj(v)) {
//获取边e的终点
int w = e.to();
//起点s到顶点w的权重是否大于起点s到顶点v的权重+边e的权重,如果大于,则修改s->w的路径:
edgeTo[w]=e,并修改distTo[v] = distTo[v]+e.weitht(),如果不大于,则忽略
if (distTo(w)>distTo(v)+e.weight()){
distTo[w]=distTo[v]+e.weight();
edgeTo[w]=e;
//如果顶点w已经存在于优先队列pq中,则重置顶点w的权重
if (pq.contains(w)){
pq.changeItem(w,distTo(w));
}else{
//如果顶点w没有出现在优先队列pq中,则把顶点w及其权重加入到pq中
pq.insert(w,distTo(w));
}
}
}
}
//获取从顶点s到顶点v的最短路径的总权重
public double distTo(int v){
return distTo[v];
}
//判断从顶点s到顶点v是否可达
public boolean hasPathTo(int v){
return distTo[v]<Double.POSITIVE_INFINITY;
}
//查询从起点s到顶点v的最短路径中所有的边
public Queue<DirectedEdge> pathTo(int v){
//如果顶点s到v不可达,则返回null
if (!hasPathTo(v)){
return null;
}
//创建队列Queue保存最短路径的边
Queue<DirectedEdge> edges = new Queue<>();
//从顶点v开始,逆向寻找,一直找到顶点s为止,而起点s为最短路劲树的根结点,所以
edgeTo[s]=null;
DirectedEdge e=null;
while(true){
e = edgeTo[v];
if (e==null){
break;
}
edges.enqueue(e);
v = e.from();
}
return edges;
}
}
//测试代码
public class DijkstraSpTest {
public static void main(String[] args) throws Exception {
//创建输入流
BufferedReader reader = new BufferedReader(new
InputStreamReader(DijkstraSpTest.class.getClassLoader().getResourceAsStream("min_route_test
.txt")));
//读取顶点数目,初始化EdgeWeightedDigraph图
int number = Integer.parseInt(reader.readLine());
EdgeWeightedDigraph G = new EdgeWeightedDigraph(number);
//读取边的数目
int edgeNumber = Integer.parseInt(reader.readLine());
//循环读取每一条边,并调用addEdge方法
for (int i = 0; i < edgeNumber; i++) {
String line = reader.readLine();
int v = Integer.parseInt(line.split(" ")[0]);
int w = Integer.parseInt(line.split(" ")[1]);
double weight = Double.parseDouble(line.split(" ")[2]);
G.addEdge(new DirectedEdge(v, w, weight));
}
//根据图G和顶点0,构建DijkstraSP对象
DijkstraSP dsp = new DijkstraSP(G, 0);
//获取起点0到顶点6的最短路径
Queue<DirectedEdge> edges = dsp.pathTo(6);
//打印输出
for (DirectedEdge edge : edges) {
System.out.println(edge.from() + "->" + edge.to() + "::" + edge.weight());
}
}
}






![2023新年祝福代码[css动画特效]](https://img-blog.csdnimg.cn/46d30533ba1f4facaa594a390b6f57c7.png)