曲线的渐近线

• 渐近线综合了极限和函数图形的知识,尤其是斜渐近线

水平和垂直渐近线

• 若点$M$沿曲线$y=f(x)$无限远离原点时,它于某条直线$L$之间的距离将趋近于0,则称该直线$L$为曲线的渐近线

• 若$L$与$x$轴平行,则该直线称为水平渐近线

  • 若$\underset{x\to \infty }{\lim }f(x)=A$(包括$x\to -\infty$,$x\to +\infty$),则$y=A$为$y=f(x)$的水平渐近线

• 若$L$与$y$轴平行,则该直线称为垂直渐近线或铅直渐近线

  • 若$\underset{x\to x_0}{\lim }f(x)=\infty$,(包括$x\to {x_0}^{-}$,$x\to {x_0}^{+}$),则$x=x_0$为$y=f(x)$的水平渐近线
  • 注意只要有一侧满足条件,就称$x=x_0$处有渐进线

斜渐近线

• 若$L$不与坐标轴平行,则该直线称为斜渐近线

  • 若$\underset{x\to \infty }{\lim }\frac{f(x)}{x}=a$且$\underset{x\to \infty }{\lim }(f(x)-ax)=b$;(包括$x\to -\infty$,$x\to +\infty$),则$y=ax+b$为$y=f(x)$的斜渐近线

斜渐近线公式推导

• 动点$(x,f(x))$到直线$L$:$y=ax+b$的距离为$d=\frac{|f(x)-ax-b|}{\sqrt{a^2+1}}$(0),
• 不妨设$f(x)$有在$x\to +\infty$时的渐近线,
  • 由渐近线性质,$d\to 0(x\to \infty )$,$\underset{x\to +\infty }{\lim }|f(x)-ax-b|=0$(1)
  • 由极限性质和式(1)可知$\underset{x\to +\infty }{\lim }(f(x)-ax-b)=0$(2),
  • 由函数加法极限运算法则:$\underset{x\to +\infty }{\lim }(f(x)-ax)=b$,(3)
• 构造$\underset{x\to +\infty }{\lim }(\frac{f(x)}{x}-a)$(4);即$\underset{x\to +\infty }{\lim }\frac{1}{x}(f(x)-ax)$=$\underset{x\to +\infty }{\lim }\frac{1}{x}$ $\cdot$ $\underset{x\to +\infty }{\lim }[f(x)-ax]$=$0\cdot b$=0,所以$\underset{x\to +\infty }{\lim }(\frac{f(x)}{x}-a)$=$0$,即$\underset{x\to +\infty }{\lim }\frac{f(x)}{x}=a$(5)
• (5),(3)两个极限,分别可求得$a,b$,也就求得了渐近线
  • $\underset{x\to +\infty }{\lim }\frac{f(x)}{x}=a$
  • $\underset{x\to +\infty }{\lim }(f(x)-ax)=b$
• 公式组表明,欲判断曲线$f(x)$的斜渐渐线,需要针对$-\infty ,+\infty$两类情形,分别构造2个极限式,两者都存在时,就可以确定有相应的渐渐线
• Note:
  • 关于式(3),还可以这样理解:于渐近线$L$平行且过原点的直线方程为$L_0:y=ax$
  • 而当$x\to \infty$时,$f(x)$与$L$在$y$轴方向上的距离$|f(x)-(ax+b)|\to 0$,
  • 即$|f(x)-ax|\to |ax+b-ax|=|b|$,所以有式(3)

简便方法确定斜渐近线(一次多项式化方法)

• 由于渐近线是直线,考虑从直线方程$y=ax+b$找新途径
• 当$x$足够大时,且$f(x)$存在渐近线时,我们可以使用渐近线来近似$f(x)$
• 一般得,若$f(x)$能够表示为$f(x)$=$ax+b+\alpha (x)$,$(a\ne 0)$,其中$\alpha (x)$是一个$x\to \infty$时得无穷小,那么就能说明$ax+b$是$f(x)$的斜渐近线
• 这种方法确定渐近线通常要搭配泰勒公式(麦克劳林公式),将非多项式多项式化
  • 可以先从被求函数$f(x)$提取出一个$x$或$|x|$
  • 对剩余部分作泰勒展开,且只需要展开到$\frac{1}{x}$(如果没有就只需要展开到常数项)就可以了,$\frac{1}{x}$的高次方无穷小可以用低次方代替,因为$o((\frac{1}{x}{)}^m)$包含$o((\frac{1}{m}{)}^n)$,$(n>m)$
  • 当然,反过来就不行,不能用高阶无穷小表示(代替)低阶无穷小

例

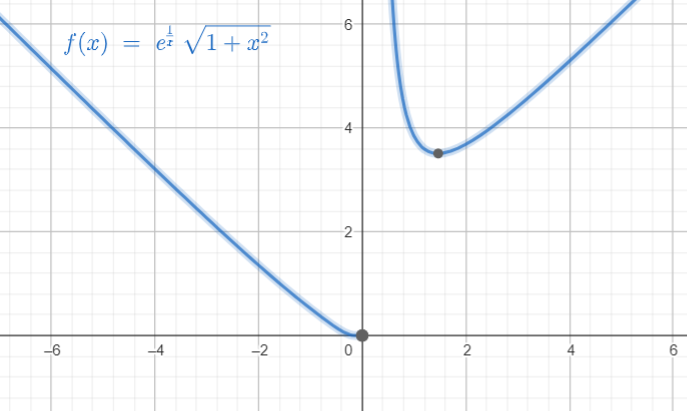
• 曲线$y$=$e^{\frac{1}{x}}\sqrt{1+x^2}$的渐进线

  • 水平渐近线:$y\to 0(x\to 0)$,因此无水平渐渐
  • 垂直渐近线:
    • 从定义域找有限值:$x\ne 0$
    • 对于$\underset{x\to 0}{\lim }y$
      • 具体要分$x\to 0^{-}$和$x\to 0^{+}$的情形
      • $\underset{x\to 0^{-1}}{\lim }y$=$1$
      • $\underset{x\to 0^{+}}{\lim }y$=$\infty$,因此$x=0$处存在垂直渐近线
  • 斜渐近线(定义法)
    • 构造$\underset{x\to +\infty }{\lim }\frac{e^{\frac{1}{x}}\sqrt{1+x^2}}{x}$=$1$=$a_1$
    • $b_1$=$\underset{x\to +\infty }{\lim }(e^{\frac{1}{x}}\sqrt{1+x^2}-a_{1}x)$=$\underset{x\to +\infty }{\lim }(e^{\frac{1}{x}}\sqrt{1+x^2}-x)$
      • 这个极限是$\infty -\infty$未定式)
      • 其计算可以通过适当的增减同一项,这里$-e^{\frac{1}{x}}x+e^{\frac{1}{x}}x$,需要一定的经验和尝试找出合适的项
      • 从而$b_1$=$\underset{x\to +\infty }{\lim }(e^{\frac{1}{x}}\sqrt{1+x^2}-e^{\frac{1}{x}}x+e^{\frac{1}{x}}x-x)$,然后适当分组:
        • $b_1$=$\underset{x\to +\infty }{\lim }(e^{\frac{1}{x}}(\sqrt{1+x^2}-x)+(e^{\frac{1}{x}}-1)x)$
          • $\underset{x\to +\infty }{\lim }{e}^{\frac{1}{x}}(\frac{1}{\sqrt{1+x^2}+x})$=$0$(分子有理化)
          • $\underset{x\to +\infty }{\lim }(e^{\frac{1}{x}}-1)x$=$1$(等价无穷小)
        • $b_1$=$0+1$=$1$
      • 因此$x\to +\infty$的渐近线为$y=x+1$
    • 类似的,可以求得另一条渐近线$x\to -\infty$为$y=-x-1$
  • 斜渐近线(一次多项式化方法)
    • $y$=$|x|e^{\frac{1}{x}}\sqrt{1+\frac{1}{x^2}}$,$(x\to \infty )$
      • =$|x|[(1+\frac{1}{x}+o(\frac{1}{x}))(1+o(\frac{1}{x}))]$
        • 这里$\sqrt{1+\frac{1}{x^2}}$=$1+o(\frac{1}{x^2})$中的无穷小可以用$o(\frac{1}{x})$代替,
      • =$|x|(1+\frac{1}{x}+o(\frac{1}{x}))$
      • =$|x|+\frac{|x|}{x}+|x|o(\frac{1}{x})$,其中$\alpha (x)$=$|x|o(\frac{1}{x})$=$\frac{o(\frac{1}{x})}{\frac{1}{|x|}}$是$x\to \infty$的无穷小
      • =$x+1$+$\alpha (x)$,$(x>0)$;或$-x-1+\alpha (x)$

• 综上,共有3条渐近线