摘要:

Goldstein枝切法作为相位解缠中路径积分法的重要算法之一，其解缠结果易受到噪声或间断相位缺陷所引起的残差点影响。为了研究相位间断缺陷对解缠算法的影响，模拟了具有间断相位缺陷的数据，采用 Gold-stein枝切法进行了系统的解缠研究。重点研究了残差点对枝切线的搜索窗口半径大小的影响，并将解缠相位与真实相位进行了比较。结果表明，在单相位间断和双不相交的相位间断缺陷的情况下，Goldstein枝切法仍然具有较好的解缠效果;对于双交叉相位间断缺陷，Goldstein枝切法在这一局部区域无法得到正确的解缠结果;通过研究枝切线搜索窗口半径对解缠的影响，验证了存在“有效枝切线搜索窗口半径”的结论。此实验结果对于采用或联合采用 Goldstein枝切法进行的相位解缠理论研究和应用具有参考价值。

引 言

作为干涉合成孔径雷达、光学干涉、核磁共振图像及新兴的光学非接触 3维测量重建的关键步骤，2维相位解缠得到了迅速的发展和广泛的应用［1-2］。如果仅仅是将 1维相位解缠的简单推广，2维相位解缠往往得不到满意的结果，因为相位解缠的结果往往与 1维分割的取向、信噪比和 2维采样率有着密切的关系［3］。在很多情况下，解缠误差会沿着水平或垂直的方向传递。因此，相位解缠的难点就在于如何能很好地消除误差对相位解缠的影响，来获取精确的解缠相位，目前常用相位解缠的方法可以主要归结为 3类:(1)基于路径积分的相位解缠［5］; (2)基于最小范数的相位解缠［6］; (3)基于网络规划的相位解缠算法［7］。噪声或间断相位在缠绕相位中较为常见，不同的解缠算法对于噪声或间断相位引起的残差处理也不尽相同，主要包括:(1)找出优化的积分路径，避开残差点造成的误差传递［1］; (2)基于缠绕相位计算解缠相位的相位梯度估算值，将残差点造成
的误差进行平差处理［6］; (3)对残差点不进行任何处理，在解缠结果中予以保留［7］;Goldstein枝切法采用第 1种方式处理，找出优化的积分路径［4］，通过建立合理的枝切线，隔绝噪声区，阻止相位残差点所造成的积分误差在整幅图像中的传递。

Goldstein枝切法是在残差点电荷平衡的条件下用枝切线将附近的残差点连接起来，或者把极性相反的残差对连接在一起，或者将多个残差点对组成的集合用枝切线连接起来［4］。通常残差点与图像边界的连线也可以使残差点达到极性平衡。Gold-stein枝切线的连线策略是尽量使得枝切线最短［3］。Goldstein枝切法作为典型的路径积分法，受间断相位影响很大［3］。与此同时，残差点的分布与枝切线的建立也有着紧密的内在联系。目前来看这类文献较少见到。本文中对这一问题展开专门的探讨和研究，通过模拟间断相位代替真实数据的相位跳变或缺失等问题，通过 3组实验来研究不同的相位间断形式(包括单间断、双间断以及交叉双间断相位 3种情况)对于解缠的影响。此外，还研究了枝切线搜索窗口半径的对解缠的影响，验证了存在“有效枝切线搜索窗口半径”的结论。

1.Goldstein枝切法相位解缠原理

从数学角度而言，解缠的目的就是要正确地将相位重建起来。1维相位解缠以一个周期内数据的
连续性为前提条件的，沿着某一个方向上计算而进行的。通常干涉雷达图像数据是 2维数据，通过两幅复数图像的配准计算出每一像素点上的干涉相位差。2维相位是对 1维相位的扩展［8］。给定一个 2维相位矩阵 φ（i，j）为了对该相位矩阵进行解缠，需要对每个点(i，j)加上或减去 2π的整数倍值，从而得到一个连续的函数（ i，j）k为整数矩阵:

给定一个 2维相位矩阵 φ（i，j），为了对该相位矩阵进行解缠，需要对每个点(i，j)加上或减去 2π的整数倍值，从而得到一个连续的函数 （i，j），k为整数矩阵:

图 1a中给出了 1维缠绕相位，其中横坐标代表它的像素序列长度，纵坐标代表的是缠绕相位值，图1b中是图 1a的解缠结果值。

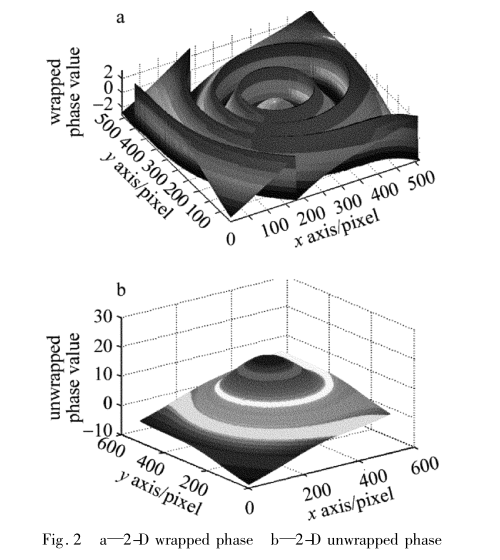
图 2a中给出了 2维缠绕相位，其中横和纵坐标代表它的像素长度，竖直 z坐标代表的是缠绕相位
值，图 2b中是图 2a的解缠结果值。

 

1． 1 残差点

实际的干涉相位数据由于噪声和不连续点的影响，会出现不同路径积分的结果。为了描述有
旋分量对相位解缠的影响，引入不连续点或残差点的概念。在一幅原始缠绕数据中，定义一个 2 × 2的窗口，以一个固定的方向，可以是顺时针或者逆时针方向，利用下面的式子计算相邻像素点之间的差值。其中 q表示的 4条边的像素差值和，Δ表示 2 × 2窗口内的每条边的像素差值，W表示缠绕操作，φ_w表示原始缠绕相位矩阵，i和 j分别为行和列值。当某一边的差值超过范围( － π，π)时，通过加减一个 2π来处理，使得每条边的差值范围都保留在 2π内，最后得到的值再除以 2π。

 若 q = 0，则定义窗口内最左上角的点(i，j)上的路径为一致性路径，否则就是不一致性路径，且这个点(i，j)称为残差点。若 q ＞ 0，表示正残差点;若q ＜ 0，表示负残差点。移动 2 × 2窗口，直到找出整幅相位图像的残差点。

1． 2 分支截断理论

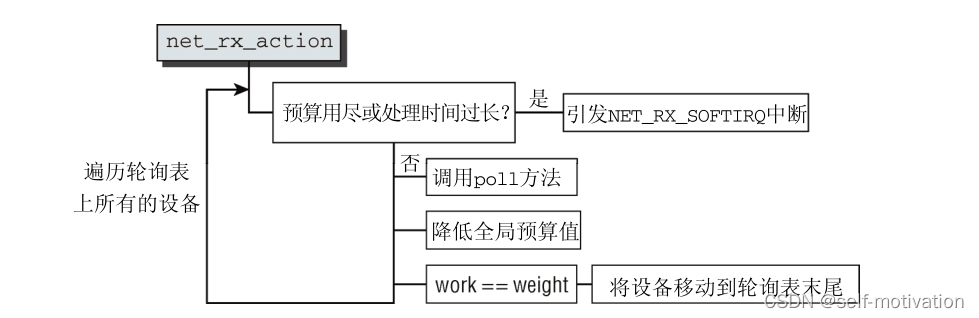
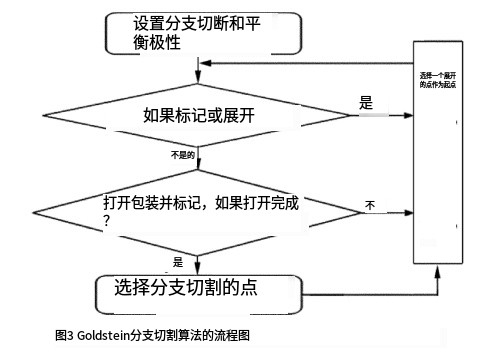
分支截断理论的典型代表就是 Goldstein枝切法，图 3是 Goldstein枝切法的流程图。通过计算相
位图像的残差点，根据残差点标注的极性建立枝切线隔离区，最后通过建立的枝切线，在已知一个解缠相位点的情况下，标注出它的 4个领域像素点［11］。通过建立的枝切线寻找最优积分路径，避开残差点所引起的误差传递。如果是在枝切线外，则利用已知的解缠相位点进行解缠绕，枝切线上的点留到最后进行解缠，这种积分方法也俗称洪水淹没法［1

Goldstein枝切法的关键在于建立合理的枝切线，一条好的枝切线可以有效地阻断相位残差点所
造成的解缠误差传递根,据残差点的分布通常可以观察判断枝切线的放置是否有错误或存在被孤
立的区域，而建立合理的枝切线又与枝切线内的搜索半径窗口有密切的关系。在枝切线搜索半径窗口设置过小，它不能穷尽搜索到所有的残差点分布;枝切线搜索半径窗口设置过大，又有可能导致连接到图像的边界，造成封闭的“孤岛”区域。

在如图 4a所示的 6个残差点中，黑色圆点表示负极性残差点，白色圆圈表示正极性残差点。图 4b
所示枝切线搜索半径窗口设置不合适，使得极性不平衡的残差点连接到图像的边界处，导致错误的枝切线。当建立图 4b中的枝切线时，在两条枝切线半径之间，其残差点误差并没有完全隔离，当解缠穿越两条枝切线之间，会导致相位跳跃的情况。图 4c中给出了正确的枝切线连接，这条枝切连线由于涵盖了图像中所有残差点，并且极性达到了平衡，有效地规避了残差点对解缠的影响。

未完待续！

参考文献：

曾凡光1 ，吴光敏1 ，MAI John D2 ，陈剑鸣1* Goldstein枝切法对存在间断相位缺陷的解缠研究    2014年 5月  激 光 技 术