图-数据结构

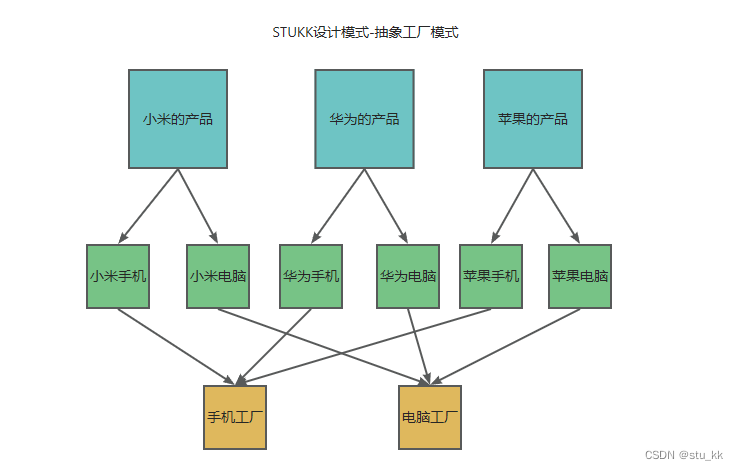
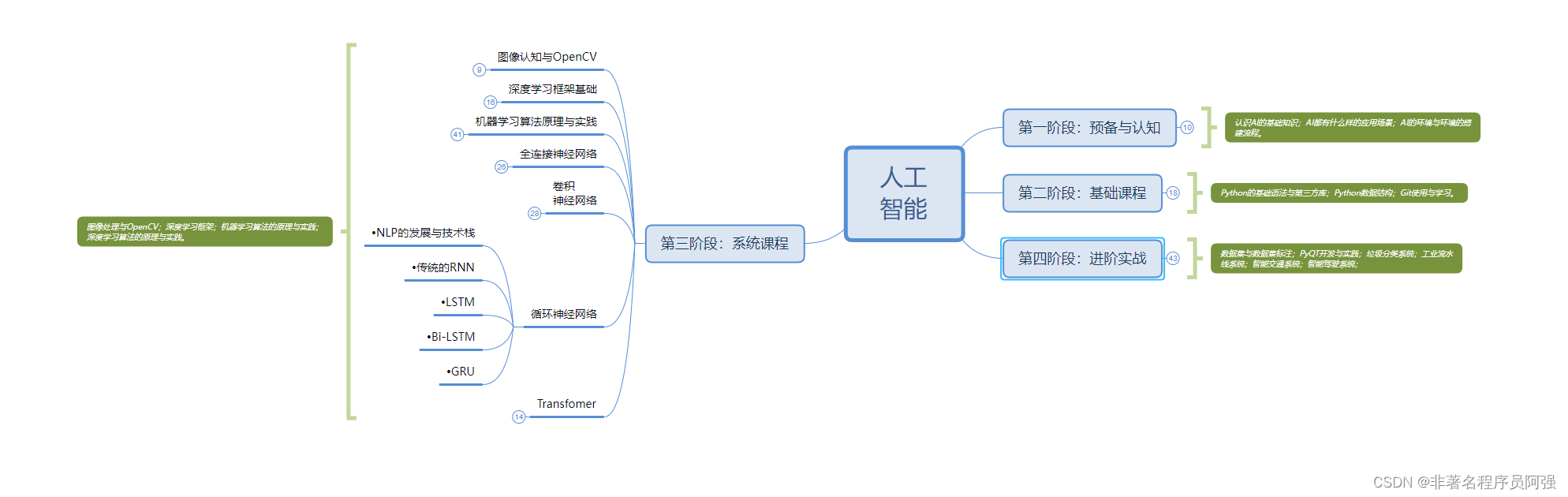
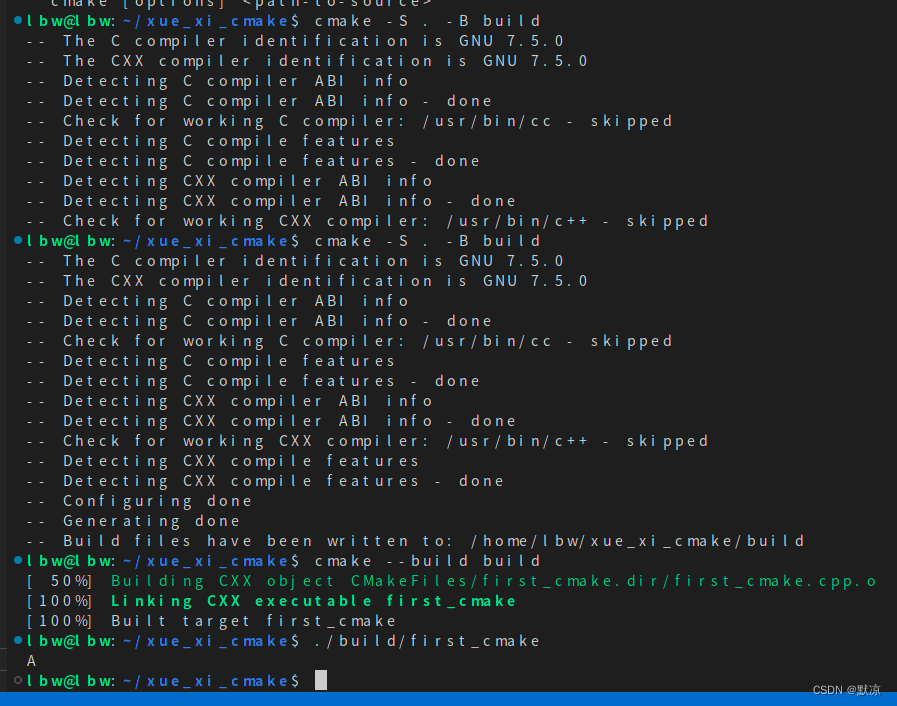
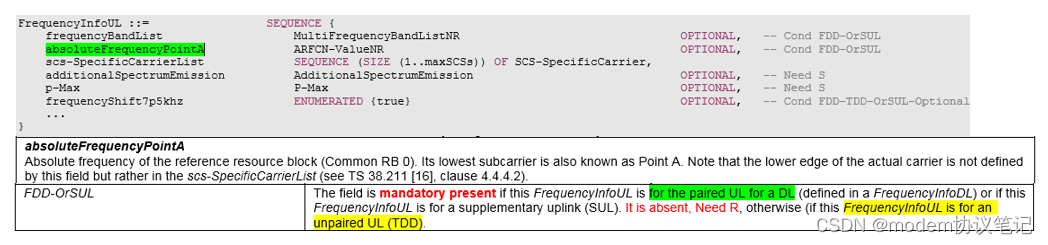
图的介绍

如果你有学过《离散数学》，那么对图的概念一定不陌生，在计算机科学中，一个图就是一些顶点的集合，这些顶点通过一系列边连接（结对）。顶点用圆圈表示，边就是这些圆圈之间的连线。注意：顶点也称为节点或交点，边也称为链接。

同时边可以是双向的，也可以是单向的，不一定所有的顶点中间一定要有边，如图：

大家都或多或少听说过最短路径算法，那你知道生活中有哪些场景出现过它的应用吗？没错，就是平常使用的地图导航软件，如图：

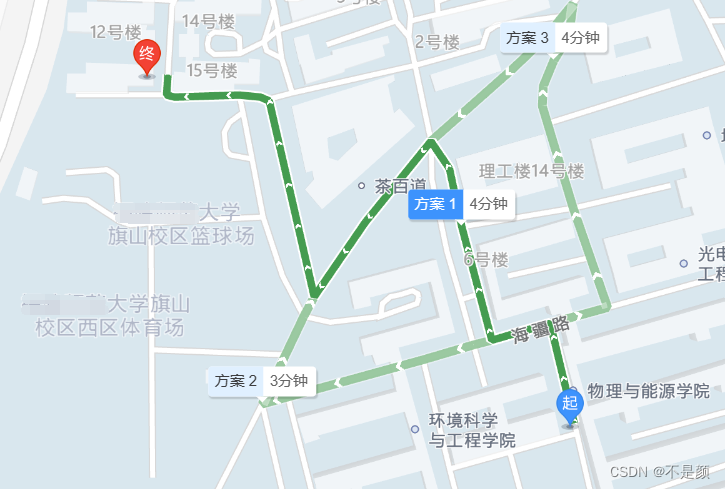
在上图中起点、终点、每一个交叉路口都可以看作是一个顶点，而连接它们的绿色通道就是边。

另外可以从图上看出，从一个地方到另一个地方有着多种路径，影响因素有距离、红绿灯、拥堵情况、事故。对于多种因素可以使用边的权重来表示，根据情况的不同给边分配数值。

我们之前学的树和链表其实都是图的特例。

图的表示方法

邻接列表

每一个顶点都会保存着与它相邻的边，并且这个边的起点是这个顶点,即只描述指向外部的边。例如下图中，B应该保存着三条边，C保存一条边，因为B有三条指向外面，而C只有一条指向外面。

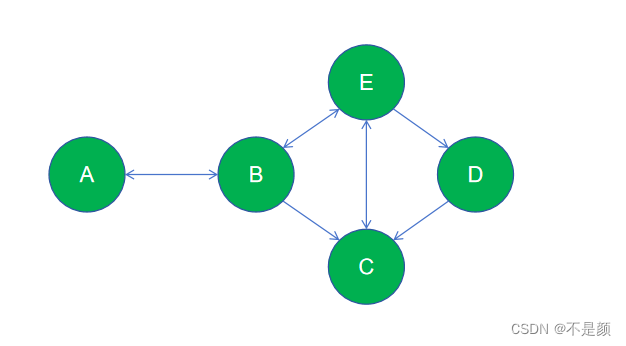
而它的邻接列表表示为：

按照这样的存储方式，想必查找两个顶点之间关系或者权重时会有点费时。

邻接矩阵

邻接矩阵由二维数组表示，行和列都表示顶点，两个顶点所对应的矩阵元素数值表示两个顶点是否相连（ 0 表示不相连，非 0 表示相连以及权重值）。

将上面的图用邻接矩阵表式则为（在这里边上无权重，所有1表示的是相连）：

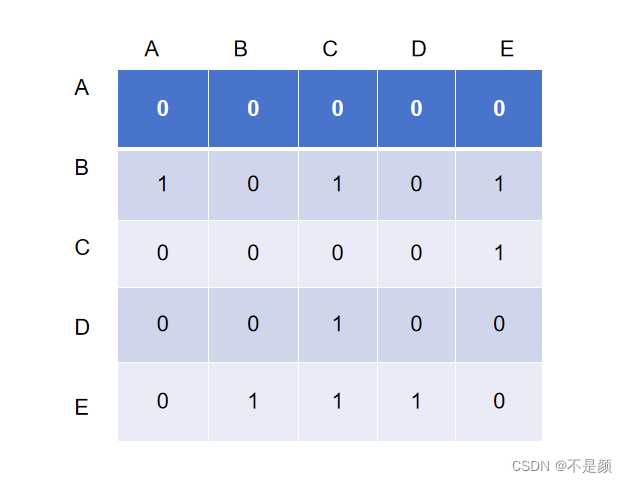
这邻接矩阵查找就特别快了，但是往里面添加顶点的成本很高，因为要重新按照新的行和列创建一个新的矩阵，然后将已有的数据复制到新矩阵中去。

使用哪个更好

操作	邻接列表	邻接矩阵
存储空间	O(V+E)	O(V^2)
添加顶点	O(1)	O(V^2)
添加边	O(1)	O(1)
检查相邻性	O(1)	O(1)

其中V表示图中顶点的个数，E表示边的个数。

结论：大多数情况选择邻接列表。除非图比较密集，即每个顶点都与大部分顶点相邻，并且个数不多，那么就选择邻接矩阵。

图的算法实现

结构体定义

首先要理清楚结构关系，这里的图中有三种结构，分别是边、顶点、邻接链表，以下是它们的定义。

#define MaxSize 1024

typedef char DateElem; //顶点中存储的元素
//边
typedef struct _EdgeNode
{
	int adjvex; //与之相邻的节点的位置
	int weight; //边的权重
	struct _EdgeNode* next; //指向下一条与这个顶点相邻的边
}EdgeNode;


//顶点
typedef struct _VertexNode
{
	DateElem date;				//顶点的数据
	struct _EdgeNode* first;    //指向第一条与之相邻的边
}VertexNode,AdjList;

//邻接链表 
typedef struct _AdjListGraph
{
	AdjList* adjlist; //数组，保存着所有的顶点
	int vex; //顶点数
	int edge;//边数
}AdjListGraph;

邻接链表结构体中有着一个数组，数组保存着各顶点，顶点中又保存着与之相邻的边，整体是这样的结构。

图的初始化

其中 visited 数组是为了接下来的遍历操作，防止重复访问节点，因为在初始化里面出现了，那就一起写上。

bool visited[MaxSize]; //节点是否被访问过，被访问过为true
void Init(AdjListGraph& G)
{
	G.adjlist = new AdjList[MaxSize]; //像哈希表的结构
	G.edge = 0;
	G.vex = 0;

	for (int i = 0; i < MaxSize; i++)
	{
		visited[i] = false;
	}
}

图的创建

因为创建一条边，需要知道起始的顶点和结束的顶点的位置，所以使用自己定义的 Location 函数，通过你输入的顶点数据，找到这个顶点在数组中的位置。

int Location(AdjListGraph& G, DateElem c);

void Create(AdjListGraph& G)
{
	cout << "请输入顶点和边的个数：";
	cin >> G.vex >> G.edge;

	cout << "请依次输入顶点的数据：";
	
	for (int i = 0; i < G.vex; i++)
	{
		cin >> G.adjlist[i].date;
		G.adjlist[i].first = NULL;
	}


	cout << "请依次输入边的起始和终点：";
	DateElem v1, v2;
	int i1 = 0 , i2 = 0;
	
	for (int i = 0; i < G.edge; i++)
	{
		cin >> v1 >> v2;

		i1 = Location(G, v1);
		i2 = Location(G, v2);

		if (i1 != -1 && i2 != -1)
		{
			EdgeNode* tmp = new EdgeNode;
			tmp->adjvex = i2;
			tmp->next = G.adjlist[i1].first;
			G.adjlist[i1].first = tmp;
		}
	}
}

//通过顶点保存的数据找到顶点在图中的位置
int Location(AdjListGraph& G, DateElem c)
{

	for (int i = 0; i < G.vex; i++)
	{
		if (G.adjlist[i].date == c)
		{
			return i;
		}
	}

	return -1; //没找到
}

其中插入节点的操作为下图所示：

相当于链表的前插法。

图的遍历

如下图，这也是一个图结构，不过这让我想到树结构，是因为图的遍历方式和树的遍历方式有很多相似之处。

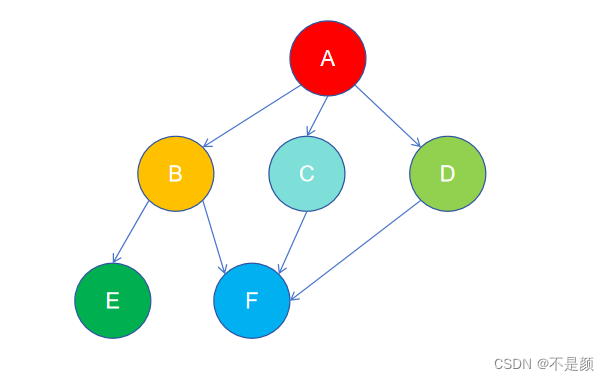
深度遍历

也就是以一个未被访问过的顶点作为起始顶点，沿当前顶点的边去访问未被访问过的顶点。

当没有未被访问过的顶点时，就回退到上一个顶点，访问别的顶点，直到所有的顶点都被访问过。

深度遍历其实迷宫问题中就出现过了，也就是这条路能走就一直走，不撞南墙不回头。

深度遍历和树的前序遍历很类似，假如起始顶点是 A，深度遍历可以是：A D F C B E，也可以是A B E F C D，只是因为输入边时的顺序不同。

//深度遍历一个节点
void DFS(AdjListGraph& G, int v)
{

	if (visited[v] == true)
	{
		return;
	}

	cout << G.adjlist[v].date << " ";
	visited[v] = true;

	EdgeNode* temp = G.adjlist[v].first;
	int cur = 0;
	while (temp != NULL)
	{
		cur = temp->adjvex; //当前节点的位置
		if (visited[cur] == false)
		{
			DFS(G, cur);
		}
		temp = temp->next;
	}

}
//深度遍历全部节点
void DFS_All(AdjListGraph& G)
{
    for (int i = 0; i < MaxSize; i++)
    {
	    visited[i] = false;
    }
	for (int i = 0; i < G.vex; i++)
	{
		if (visited[i] == false)
		{
			DFS(G, i);
		}
	}
}

广度遍历

首先以一个未被访问过的顶点作为起始顶点，访问其相邻的所有顶点。

然后对每个相邻的顶点，再访问它们相邻的未被访问过的顶点，直至所有顶点都被访问过，遍历结束。

广度遍历有点像树的层序遍历，例如 A 为起始顶点，那么广度遍历的结果可能是：A D C B F E 或者是：A B C D E F 。

//广度优先遍历 需要包含头文件 <queue> 
void BFS(AdjListGraph& G, int v)
{
	queue<int> q;
	q.push(v);

	int cur = -1;
	while (!q.empty())
	{
		cur = q.front(); //取队头元素
		q.pop(); //出队

		if (visited[cur] == false)
		{
			cout << G.adjlist[cur].date << " ";
			visited[cur] = true;
		}

		
        //将与 cur 顶点相邻的顶点都入队
		EdgeNode* tmp = G.adjlist[cur].first; 
		while (tmp != NULL)
		{
			q.push(tmp->adjvex);
			tmp = tmp->next;
		}


	}
}
void BFS_All(AdjListGraph& G)
{
	for (int i = 0; i < MaxSize; i++) //初始化
	{
		visited[i] = false;
	}

	for (int i = 0; i < G.vex; i++)
	{
		if (visited[i] == false)
		{
			BFS(G, i);
		}
	}
}

用上图的图作为演示，得到运行结果。

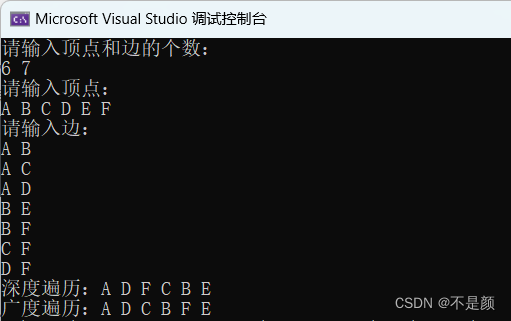
其实从它们的叫法中也能看出一些来。

全部代码

#include <iostream>
#include <queue>
using namespace std;

#define MaxSize 1024
typedef char DateElem;
//边
typedef struct _EdgeNode
{
	int adjvex; //与之相邻的节点
	int weight; //边的权重
	struct _EdgeNode* next; //指向下一条与这个顶点相邻的边
}EdgeNode;


//顶点
typedef struct _VertexNode
{
	DateElem date;				//顶点的数据
	struct _EdgeNode* first;//指向第一条与之相邻的边
}VertexNode,AdjList;

//邻接链表 
typedef struct _AdjListGraph
{
	AdjList* adjlist; //数组，保存着所有的顶点
	int vex; //顶点数
	int edge;//边数
}AdjListGraph;



bool visited[MaxSize]; //节点是否被访问过，被访问过为true
//图的初始化
void Init(AdjListGraph& G)
{
	G.adjlist = new AdjList[MaxSize]; //像哈希表
	G.edge = 0;
	G.vex = 0;

	for (int i = 0; i < MaxSize; i++)
	{
		visited[i] = false;
	}
}


int Location(AdjListGraph& G, DateElem c);
//图的创建
void Create(AdjListGraph& G)
{
	cout << "请输入顶点和边的个数："<<endl;
	cin >> G.vex >> G.edge;

	cout << "请输入顶点：" << endl;
	
	for (int i = 0; i < G.vex; i++)
	{
		cin >> G.adjlist[i].date;
		G.adjlist[i].first = NULL;
	}


	cout << "请输入边：" << endl;
	DateElem v1, v2;
	int i1 = 0 , i2 = 0;
	
	for (int i = 0; i < G.edge; i++)
	{
		cin >> v1 >> v2;

		i1 = Location(G, v1);
		i2 = Location(G, v2);

		if (i1 != -1 && i2 != -1)
		{
			EdgeNode* tmp = new EdgeNode;
			tmp->adjvex = i2;
			tmp->next = G.adjlist[i1].first;
			G.adjlist[i1].first = tmp;
		}
	}
}

//通过顶点保存的数据找到顶点在图中的位置
int Location(AdjListGraph& G, DateElem c)
{

	for (int i = 0; i < G.vex; i++)
	{
		if (G.adjlist[i].date == c)
		{
			return i;
		}
	}

	return -1; //没找到
}


//图的遍历，深度和广度

//深度遍历一个节点
void DFS(AdjListGraph& G, int v)
{

	if (visited[v] == true)
	{
		return;
	}

	cout << G.adjlist[v].date << " ";
	visited[v] = true;

	EdgeNode* temp = G.adjlist[v].first;
	int cur = 0;
	while (temp != NULL)
	{
		cur = temp->adjvex; //当前节点的位置
		if (visited[cur] == false)
		{
			DFS(G, cur);
		}
		temp = temp->next;
	}

}
//深度遍历全部节点
void DFS_All(AdjListGraph& G)
{
	for (int i = 0; i < MaxSize; i++)
	{
		visited[i] = false;
	}

	for (int i = 0; i < G.vex; i++)
	{
		if (visited[i] == false)
		{
			DFS(G, i);
		}
	}
}


//广度优先遍历 包含头文件 <queue> 
void BFS(AdjListGraph& G, int v)
{
	queue<int> q;

	q.push(v);

	int cur = -1;
	while (!q.empty())
	{
		cur = q.front(); //取队头元素
		q.pop();

		if (visited[cur] == false)
		{
			cout << G.adjlist[cur].date << " ";
			visited[cur] = true;
		}

		
		EdgeNode* tmp = G.adjlist[cur].first; 
		while (tmp != NULL)
		{
			q.push(tmp->adjvex);
			tmp = tmp->next;
		}


	}
}
void BFS_All(AdjListGraph& G)
{
	for (int i = 0; i < MaxSize; i++)
	{
		visited[i] = false;
	}

	for (int i = 0; i < G.vex; i++)
	{
		if (visited[i] == false)
		{
			BFS(G, i);
		}
	}
}

int main(void)
{

	AdjListGraph G;

	//图的初始化
	Init(G);

	//图的创建
	Create(G);

	//图的遍历：深度遍历
	cout << "深度遍历：";
	DFS_All(G);

	cout << endl;

	//图的遍历：广度遍历
	cout << "广度遍历：";
	BFS_All(G);
	return 0;
}