SLAM学习——相机模型（针孔+鱼眼）

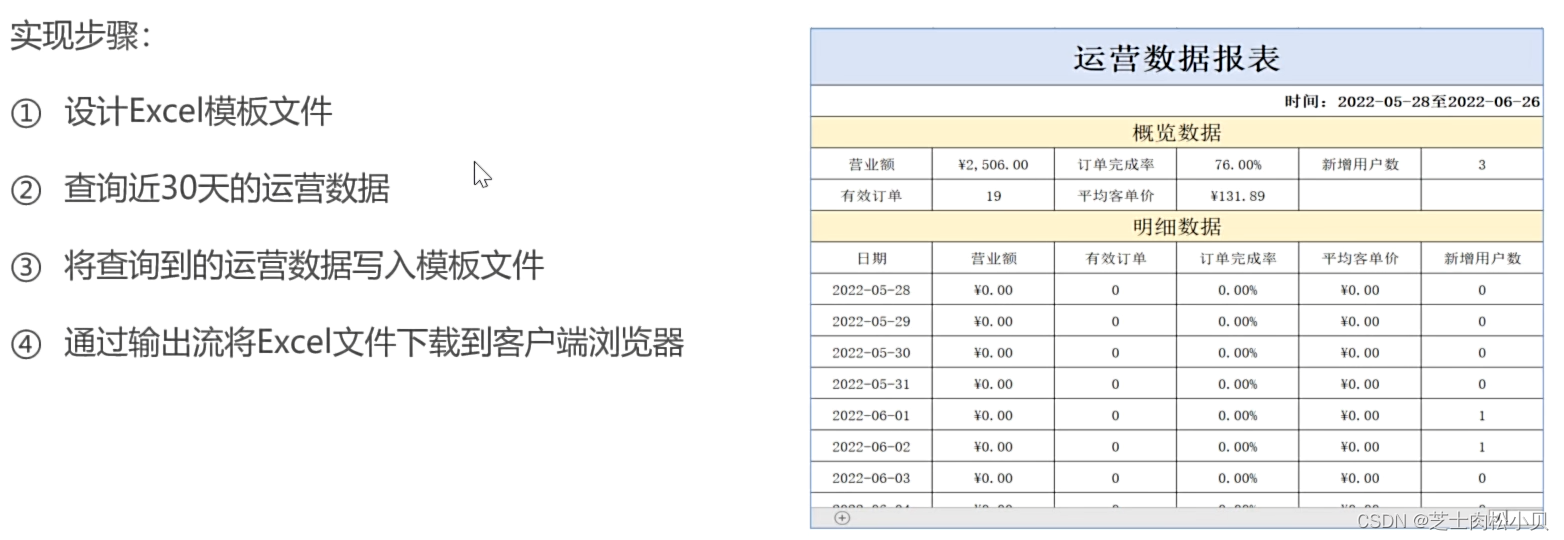
针孔相机模型

针孔相机模型是很常用，而且有效的模型，它描述了一束光线通过针孔之后，在针孔背面投影成像的关系，基于针孔的投影过程可以通过针孔和畸变两个模型来描述。
请添加图片描述
模型中有四个坐标系，分别为world，camera，image，pixel

world为世界坐标系，可以任意指定 $x_w$ 轴和 $y_w$ 轴，为上图P点所在坐标系。
camera为相机坐标系，原点位于小孔， $z_c$ 轴与光轴重合， $x_c$ 轴和 $y_c$ 轴平行投影面，为上图坐标系 $X_cY_cZ_c$ 。
- 归一化坐标系，原点位于 $z_c=1$ ，x和y轴与相机坐标系一样。
image为图像坐标系，原点位于光轴和投影面的交点， $x$ 轴和 $y$ 轴平行投影面，为上图坐标系 $x y$ ，相对于camera相差一个缩放。
pixel为像素坐标系（opencv定义），从小孔向投影面方向看，投影面的左上角为原点， $uv$ 轴和投影面两边重合，该坐标系与图像坐标系处在同一平面，但原点不同，相对于image相差一个平移。

投影变换

正投影（空间点->图像点）

**注意：**坐标变换过程使用的是齐次坐标

world->camera

设点在world中的坐标为 $P_w = (x_w,y_w,z_w)^T$ ，在camera中的坐标为 $P_c = (x_c,y_c,z_c)^T$
$\begin{bmatrix} P_c\\1 \end{bmatrix}= T^c_w \begin{bmatrix} P_w\\1 \end{bmatrix}$
其中 $T^c_w$ 为外参，即世界坐标系相对于相机坐标系的变换。
camera->归一化相机系

相机坐标系为 $F_s$ ，设一平面位于相机坐标camera的 $z = 1$ 上，为归一化平面，其坐标系 $C$ 为归一化坐标系。

根据相似三角形，P点在归一化坐标系的坐标为
$P_n = \begin{bmatrix} x_c/z_c\\y_c/z_c\\z_c/z_c \end{bmatrix} =\begin{bmatrix} x_n\\y_n\\1 \end{bmatrix}$
归一化相机系->camera->pixel

请添加图片描述

设置图像坐标系上坐标为 $P_i$ ，基于图中相似三角形（一般所得图像已经经过处理，完成翻转）可得点P在图像坐标系上坐标为：
$\frac{x_i}{f} = \frac{x_c}{z_c} = x_n, \frac{y_i}{f} = \frac{y_c}{z_c} = y_n$
设 $\alpha$ 和 $\beta$ 分别为x和y方向上的每米像素值，设图像中心偏移为 $c_x,c_y]$ ，设像素坐标 $P_{uv} = (u,v,1)^T$ ，则
$\alpha x_i+c_x = \alpha f x_n +c_x,v = \beta y_i+c_y = \beta f y_n +c_y$
设 $f_x = \alpha f, f_y = \beta f$ ，即
$P_{uv} = \begin{bmatrix} f_x&0&c_x\\0&f_y&c_y\\0&0&1 \end{bmatrix}P_n = K P_n$
其中K为内参数矩阵(Camera Intrinsics)。

因此world到pixel到关系为
$P_{uv}=K_{3 \times 3}T^C_WP_w$
其中隐含了一次齐次坐标到非齐次坐标的转换，具体坐标系变换流程为
$世界坐标系\rightarrow 相机坐标系( 归一化处理)\rightarrow 图像坐标系 \rightarrow 像素坐标系\\ world \rightarrow camrea \rightarrow image \rightarrow pixel\\ P_w = (x_w,y_w,z_w,1)^T\rightarrow P_c = (x_c,y_c,z_c,1)^T [P_i = (x_i,y_i,1)^T ]\rightarrow P_{uv} = (u,v,1)^T$

//Parameters vector corresponds to
//      [fx, fy, cx, cy]
// 归一化平面->pixel
Eigen::Vector2d Pinhole::project(const Eigen::Vector3d &v3D) {
    Eigen::Vector2d res;
    res[0] = mvParameters[0] * v3D[0] / v3D[2] + mvParameters[2];
    res[1] = mvParameters[1] * v3D[1] / v3D[2] + mvParameters[3];

    return res;
}

反投影（图像点->空间点）

设已知图像点在相机坐标系下的深度为Z
$P_w = T^w_c Z K^{-1} P_{uv}$

//Parameters vector corresponds to
//      [fx, fy, cx, cy]
// pixel->归一化平面
cv::Point3f Pinhole::unproject(const cv::Point2f &p2D) {
    return cv::Point3f((p2D.x - mvParameters[2]) / mvParameters[0], (p2D.y - mvParameters[3]) / mvParameters[1],1.f);
}

畸变

一般使用的去畸变处理方法：先对整张图像去畸变，得到去畸变后的图像，然后讨论图像上点的空间位置。
$\begin{cases} x_{corrected} =x(1+k_1r^2+k_2r^4+k_3r^6)+2p_1xy+p_2(r^2+2x^2) \\ y_{corrected} =y(1+k_1r^2+k_2r^4+k_3r^6)+p_1(r^2+2y^2)+2p_2xy \end{cases}$
上式为对归一化平面上的点进行径向畸变和切向畸变纠正，其中k1、k2、k3为径向畸变，p1、p2为切向畸变，根据需求可以调整使用的参数，不一定要五个全用上。

径向畸变

径向畸变（桶形畸变和枕形畸变）产生原因：光线在远离透镜中心的地方偏折更大，矫正公式：
$\begin{cases} x_{corrected} =x(1+k_1r^2+k_2r^4+k_3r^6) \\ y_{corrected} =y(1+k_1r^2+k_2r^4+k_3r^6) \end{cases}$
请添加图片描述

切向畸变

切向畸变产生原因：相机组装过程不能使透镜和成像平面严格平行引起，矫正公式：
$\begin{cases} x_{corrected} =x+2p_1xy+p_2(r^2+2x^2) \\ y_{corrected} =y+p_1(r^2+2y^2)+2p_2xy \end{cases}$
请添加图片描述

小结

综上，16个单目相机的参数：

10个内部参数（内参，只与相机有关）：
- 5个内部矩阵参数K： $f,d_x,d_y,u_0,v_0$ （也可视作4个参数 $f_x,f_y,u_0,v_0$ ）
- 5个畸变参数D： $k_1,k_2,k_3,p_1,p_2$
6个外部参数（外参，描述目标点的世界坐标到像素坐标的投影关系）：
- 3个旋转参数R
- 3个平移参数t

鱼眼相机模型

请添加图片描述
鱼眼相机与针孔相机原理不同，采用非相似成像，在成像过程中引入畸变，通过对直径空间的压缩，突破成像视角的局限，从而达到广角成像，所以鱼眼镜头是一种极端得广角镜头，通常焦距小于等于16mm并且视角接近或等于180°（在工程上视角超过140°的镜头即统称为鱼眼镜头）。

鱼眼相机成像模型近似为单位球面投影模型，一般将鱼眼相机成像过程分解成两步：

先将三维空间点线性的投影到虚拟单位球面上
随后将单位球面上的点投影到图像平面上，这个过程是非线性的

由于鱼眼相机所成影像存在畸变，其中径向畸变非常严重，因此其畸变模型主要考虑径向畸变。
请添加图片描述
鱼眼相机的投影函数是为了尽可能将庞大的场景投影到有限的图像平面所设计的。根据投影函数的不同，鱼眼相机的设计模型大致分为

等距投影
$r_d = f \theta$
等立体角投影
$r_d = 2 f \sin(\frac{\theta}{2})$
正交投影
$r_d = 2 f \sin(\theta)$
体视投影
$r_d = 2 f \tan(\theta)$

相机的成像模型实际上表征的是成像的像高与入射角之间的映射关系。
请添加图片描述

通用鱼眼相机模型-Kannala-Brandt

Kannala-Brandt模型主要用于第二步，单位球面上的点投影到图像平面，该步骤为非线性，不同投影可以统一为
$r_d =f\theta _d$
因sin，tan的泰勒展开都是奇次项形式，取前5项可得
$\theta_d= k_0\theta + k_1 \theta^3 + k_2 \theta^5 + k_3 \theta^7 + k_4 \theta^9$

正投影（空间点->图像点）

世界系->归一化相机系

设外参为 $T^c_w$
$\left[ \begin{array}{c} X_c \\ Y_c \\ Z_c \end{array} \right]=R \left[\begin{array}{c} X_w \\ Y_w \\ Z_w \end{array}\right]+t\\ x_c = \frac{X_c}{Z_c},\ y_c=\frac{Y_c}{Z_c}$
归一化相机系->虚拟单位球面

$r^2 = x^2_c + y^2_c\\ \theta = arctan(r)\\ \theta _d = k_0\theta + k_1 \theta^3 + k_2 \theta^5 + k_3 \theta^7 + k_4 \theta^9\\ x_d=\frac{\theta_d}{r}x_c, \ y_d=\frac{\theta_d}{r}y_c$

虚拟单位球面->图像系
$u=f_xx_d+c_x, \ v=f_yy_d+c_y$
变换后为拉伸变形图像。
```
// Parameters vector corresponds to
// [fx, fy, cx, cy, k0, k1, k2, k3]    
// 相机系->图像系
Eigen::Vector2f KannalaBrandt8::project(const Eigen::Vector3f &v3D) {
    const float x2_plus_y2 = v3D[0] * v3D[0] + v3D[1] * v3D[1];
    const float theta = atan2f(sqrtf(x2_plus_y2), v3D[2]);
    const float psi = atan2f(v3D[1], v3D[0]);

    const float theta2 = theta * theta;
    const float theta3 = theta * theta2;
    const float theta5 = theta3 * theta2;
    const float theta7 = theta5 * theta2;
    const float theta9 = theta7 * theta2;
    const float r = theta + mvParameters[4] * theta3 + mvParameters[5] * theta5
                    + mvParameters[6] * theta7 + mvParameters[7] * theta9;

    Eigen::Vector2f res;
    res[0] = mvParameters[0] * r * cos(psi) + mvParameters[2];
    res[1] = mvParameters[1] * r * sin(psi) + mvParameters[3];

    return res;
}
```

反投影（图像点->空间点）

图像系->虚拟单位球面

$x_d = \frac{u-c_x}{f_X},y_d = \frac{v-c_y}{f_y}$
虚拟单位球面->归一化相机系->相机系
$\theta _d = \sqrt{x_d^2+y_d^2}$
使用牛頓法 (Newton’s method)求解 $\theta$
$\theta = Newton(\theta_d.k_1,k_2,k_3,k_4)$

$x_c =\frac{\tan{\theta}}{\theta_d} * x_d, y_c =\frac{\tan{\theta}}{\theta_d} * y_d$

设相机系下深度为Z
$P_c = \left[ \begin{array}{c} X_c \\ Y_c \\ Z_c \end{array} \right] = Z \left[ \begin{array}{c} x_c \\ y_c \\ 1 \end{array} \right]$

相机系->世界系
$P_w = T^w_c P_c$

// Parameters vector corresponds to
// [fx, fy, cx, cy, k0, k1, k2, k3]
// 图像系->归一化相机系
cv::Point3f KannalaBrandt8::unproject(const cv::Point2f &p2D) {
    //Use Newthon method to solve for theta with good precision (err ~ e-6)
    cv::Point2f pw((p2D.x - mvParameters[2]) / mvParameters[0], (p2D.y - mvParameters[3]) / mvParameters[1]);
    float scale = 1.f;
    float theta_d = sqrtf(pw.x * pw.x + pw.y * pw.y);
    theta_d = fminf(fmaxf(-CV_PI / 2.f, theta_d), CV_PI / 2.f);

    if (theta_d > 1e-8) {
        //Compensate distortion iteratively
        float theta = theta_d;

        for (int j = 0; j < 10; j++) {
             float theta2 = theta * theta, theta4 = theta2 * theta2, theta6 = theta4 * theta2, theta8 =
                   theta4 * theta4;
             float k0_theta2 = mvParameters[4] * theta2, k1_theta4 = mvParameters[5] * theta4;
             float k2_theta6 = mvParameters[6] * theta6, k3_theta8 = mvParameters[7] * theta8;
             float theta_fix = (theta * (1 + k0_theta2 + k1_theta4 + k2_theta6 + k3_theta8) - theta_d) /
                                  (1 + 3 * k0_theta2 + 5 * k1_theta4 + 7 * k2_theta6 + 9 * k3_theta8);
             theta = theta - theta_fix;
             if (fabsf(theta_fix) < precision)
                 break;
         }
         //scale = theta - theta_d;
         scale = std::tan(theta) / theta_d;
    }

    return cv::Point3f(pw.x * scale, pw.y * scale, 1.f);
}