生产上有用户反映，登录之后页面信息加载不出来，请求响应时间慢等。
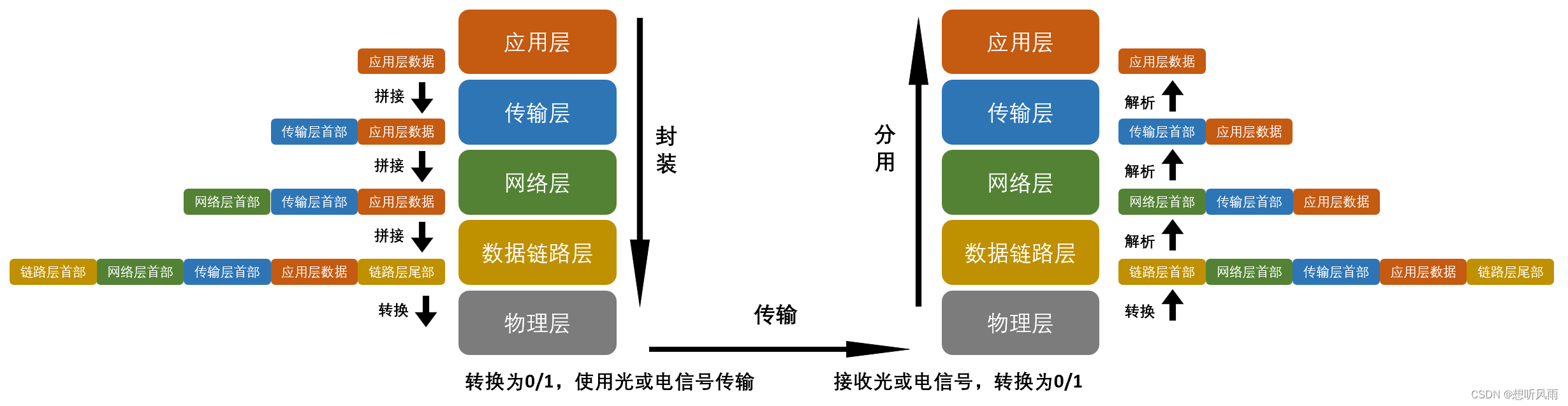
下图为生产上一个请求在网关上面的流程：

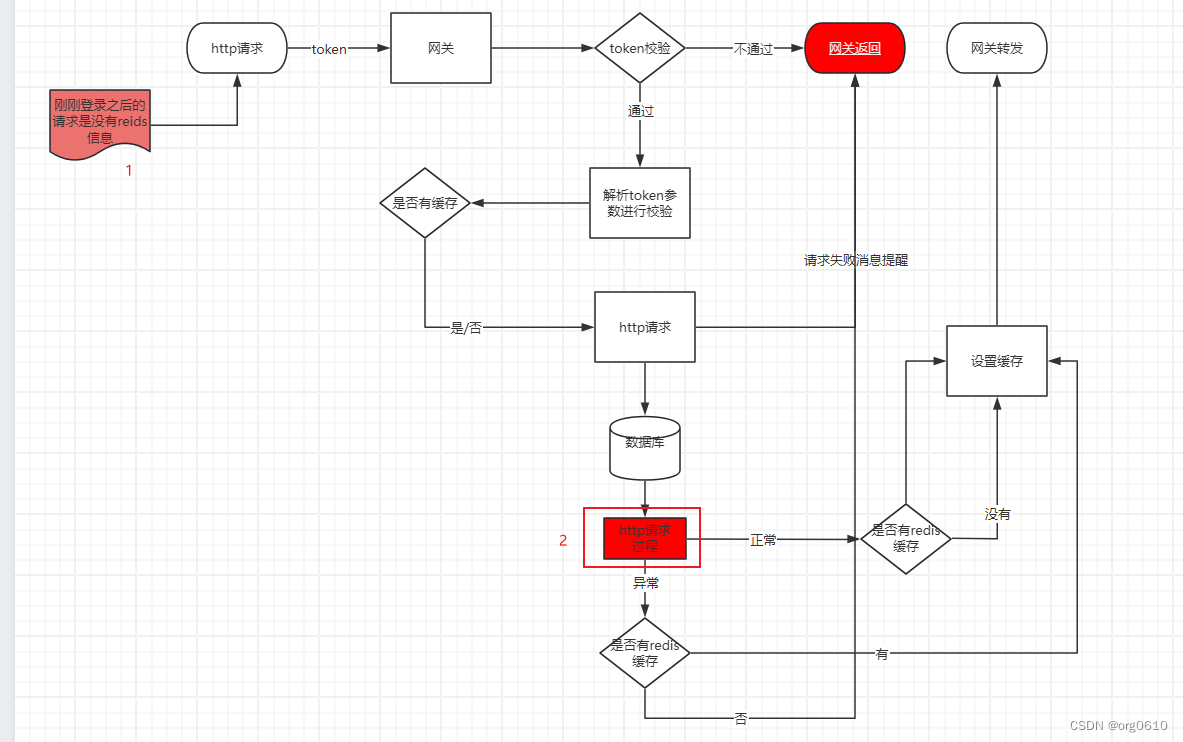
因为我们生产上，有一张异常信息记录表，第一时间查询了上面是否有最近的异常记录。发现了一点，是上图2中，接口公用的这里报错了，有一个null异常，发现出现异常的位置是请求的附件出现了问题。到这其实问题已经是发现的差不多了。

其实如果没有上面的异常记录，第一时间不熟悉网关的流程图，根本就不能这么快速的发送问题点出现在哪里，正常的思路是，按照网关的过滤流程，走一步排除是不是中间哪里的流程出现了问题，如果中间的流程没有问题，是否是请求转发到应用之后哪里出现了，这个就需要更加具体的分析了。
不过我们这里有一个重要的提示是，登录之后访问不了。我们登录和网关是分开的，登录之后生成的token可以供网关校验，但是在登录并没有走后续的token参数解析校验，所以这个问题肯定是出现在网关的流程中。要快速找到问题，对应这种网关的流程走向，应用中的服务间调用，要熟悉其流程，才能更快的找到问题所在。