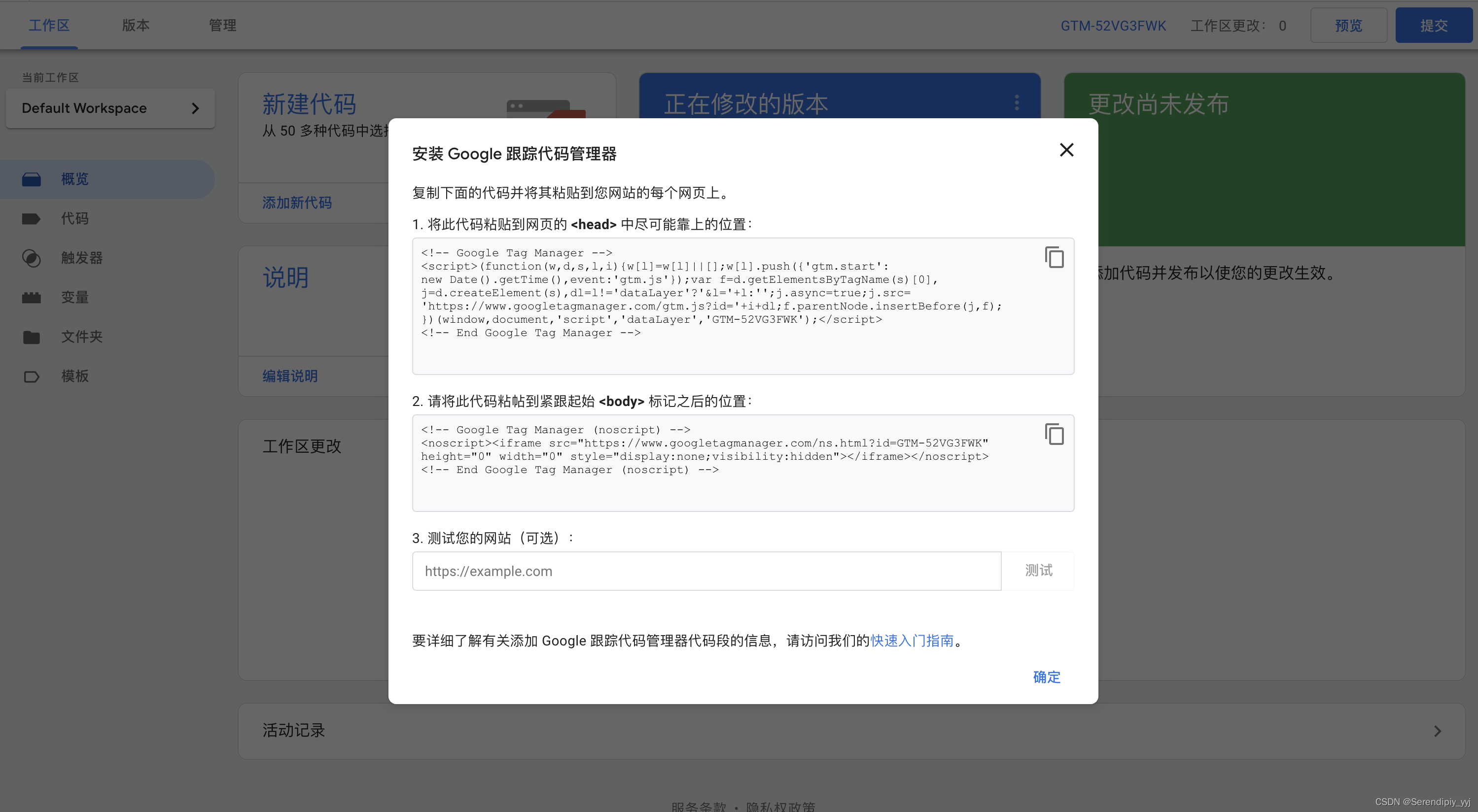
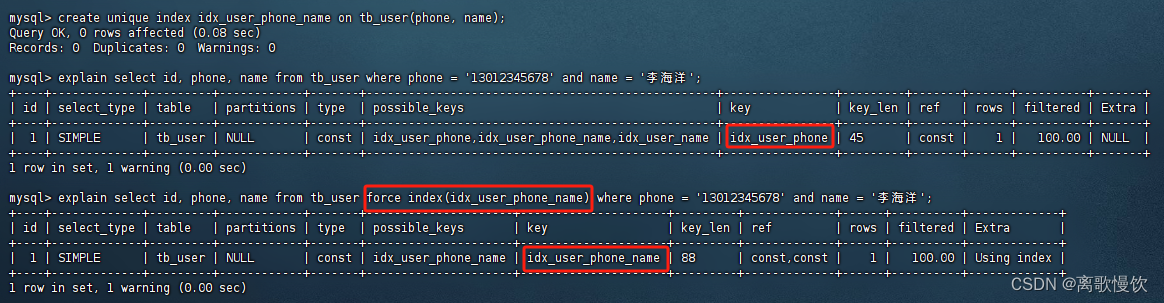
文章目录
- 📚关于DH密钥交换算法
- 📚实验目的
- 📚流程梳理
- 🐇Step1:实现快速幂取模运算
- 🐇Step2:根据算法原理分别定义公钥和共享密钥的计算
- 🐇Step3:求解问题一
- 🐇Step4:求解问题二
- 📚实验结果
📚关于DH密钥交换算法
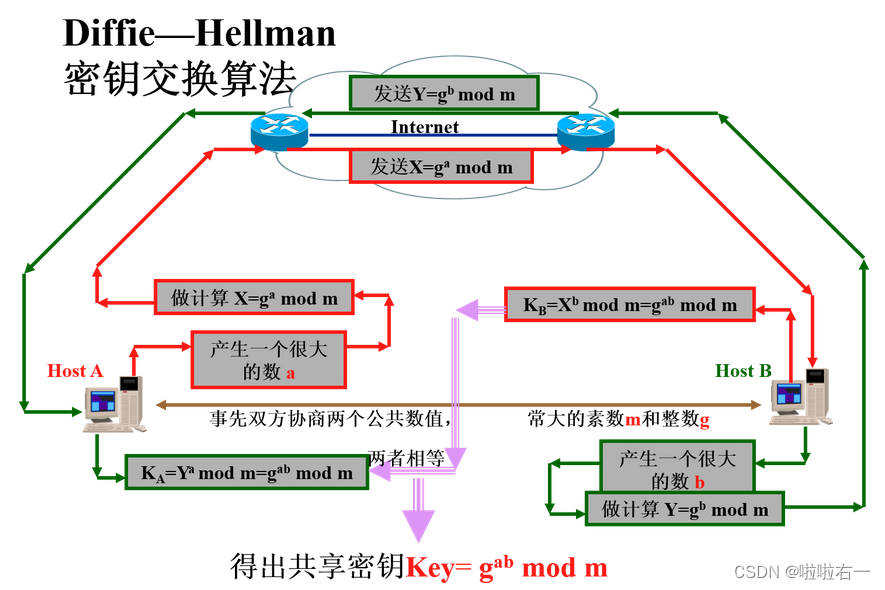
- DH密钥交换算法的核心思想是通过一种数学算法,让两个通信方在不用将密钥直接传输的情况下,协商出一个相同的密钥,用于之后的加密通信。
- 原理:通信双方先协商好两个公共数值,p和g,选取最大素数
p,再选取Z/(p)的一个本原根g,并将p和g公开,全网可用,即所有用户均可获取,并为所有用户共有。- 首先用户A随机生成一个大数a,
- 用户A计算
K1=g^a(mod p ),并将此结果传送给用户B - 用户B随机生成一个大数b
- 用户B计算
K2=g^b(mod p),并将结果传送给用户A - 用户A计算
K=(K2)^a(mod p) - 用户B计算
K = (k1) ^b(mod p) - 最终得到双方的会话密钥K
- 优点:
- 任何两个人都可以协商出会话密钥,不需要事先拥有对方的公开或者秘密的信息。
- 每次密钥交换后不必要再保留秘密信息,减少了保密的负担。
- 缺点:容易收到中间人攻击。
📚实验目的
编程实现Diffie-Hellman密钥交换算法,设有用户A和B交换密钥。
(1)设公用素数q=71,本原根α= 7。
- 若用户A的私钥XA=5,则A的公钥YA为多少?
- 若用户B的私钥XB=12,则B的公钥YB为多少?
- 共享的密钥为多少?
(2)设公用素数q=11,本原根α=2。
- 若用户A的公钥YA=9,则A的私钥XA为多少?
- 若用户B的公钥YB=3,则共享的密钥K为多少?
📚流程梳理
🐇Step1:实现快速幂取模运算
- 实现快速幂取模运算,返回 (base^exp) % mod。
def mod_exp(base, exp, mod): result = 1 # 将底数取模,防止中间结果过大 base = base % mod while exp > 0: # 当指数大于0时循环 if exp % 2 == 1: # 若指数的当前位为1 result = (result * base) % mod # 将当前的底数乘到结果中,并对模取余 exp = exp // 2 # 将指数右移一位,相当于除以2 base = (base * base) % mod # 底数取平方并对模取余 return result
🐇Step2:根据算法原理分别定义公钥和共享密钥的计算

# 计算公钥
def calculate_public_key(alpha, private_key, q):
return mod_exp(alpha, private_key, q)
# 计算共享的密钥
def calculate_shared_key(public_key, private_key, q):
return mod_exp(public_key, private_key, q)
🐇Step3:求解问题一
print("问题一结果:")
# 设公用素数q=71,本原根α= 7。
q1 = 71
alpha1 = 7
# 用户A的私钥XA=5
XA1 = 5
# 求解公钥YA
YA1 = calculate_public_key(alpha1, XA1, q1)
print("用户 A 的公钥 YA1:", YA1)
# 用户B的私钥XB=12
XB1 = 12
# 求解公钥YB
YB1 = calculate_public_key(alpha1, XB1, q1)
print("用户 B 的公钥 YB1:", YB1)
# 共享的密钥
shared_key1 = calculate_shared_key(YB1, XA1, q1)
print("共享的密钥:", shared_key1)
🐇Step4:求解问题二
print("问题二结果:")
# 设公用素数q=11,本原根α=2。
q2 = 11
alpha2 = 2
# 用户A的公钥YA=9,求解A的私钥
YA2 = 9
XA2 = 0
while calculate_public_key(alpha2, XA2, q2) != YA2:
XA2 += 1
print("用户 A 的私钥 XA2:", XA2)
# 用户B的公钥YB=3,求解共享的密钥K
YB2 = 3
shared_key2 = calculate_shared_key(YB2, XA2, q2)
print("共享的密钥:", shared_key2)
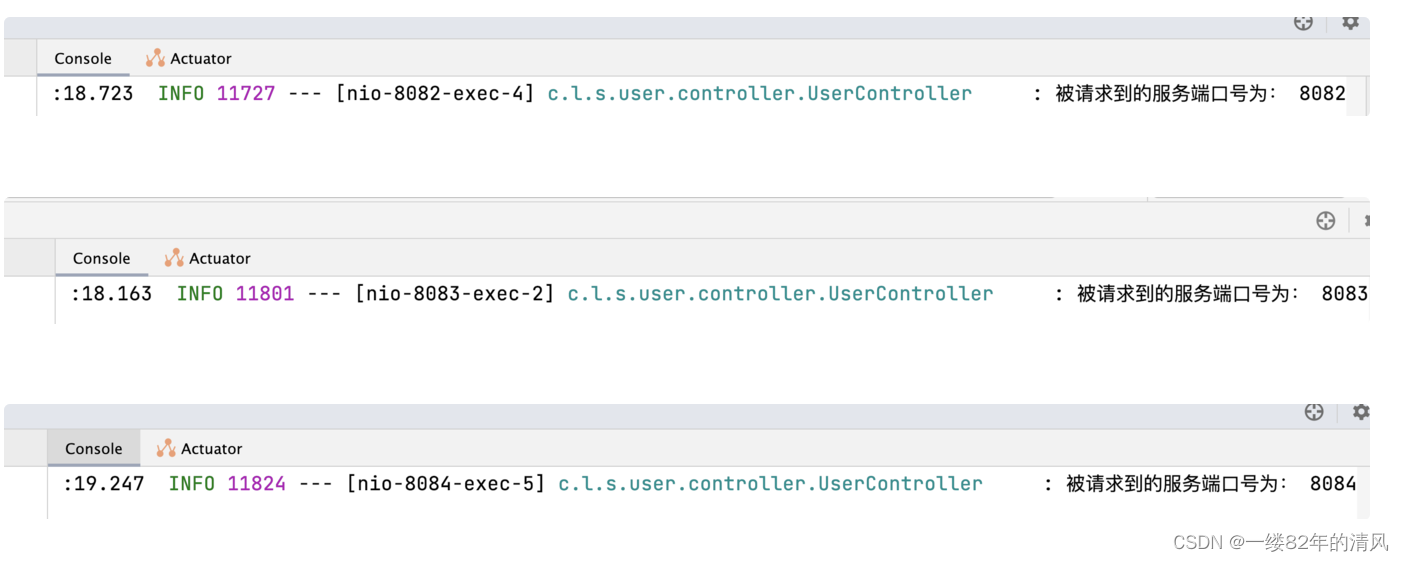
📚实验结果

参考博客:网络安全期末复习3】Diffie-Hellman密钥交换算法