• 说明：该文属于 大前端全栈架构白宝书专栏，目前阶段免费，如需要项目实战或者是体系化资源，文末名片加V！
• 作者：哈哥撩编程，十余年工作经验, 从事过全栈研发、产品经理等工作，目前在公司担任研发部门CTO。
• 荣誉：2022年度博客之星Top4、2023年度超级个体得主、谷歌与亚马逊开发者大会特约speaker、全栈领域优质创作者。

---

• 🏆 白宝书系列
  • 🏅 启示录 - 攻城狮的自我修养
  • 🏅 Python全栈白宝书
  • 🏅 ChatGPT实践指南白宝书
  • 🏅 产品思维训练白宝书
  • 🏅 全域运营实战白宝书
  • 🏅 大前端全栈架构白宝书

---

---

⭐ 指定函数上下文

先来看一个例子：

下面代码中的sum()函数可以统计学生的成绩总分：

function sum() {
    console.log(this.chinese + this.math + this.english);
}
var xiaoming = {
    chinese: 80,
    math: 95,
    english: 93
};

那么如何使用sum()函数来统计“小明”的总分呢？我们只要让xiaoming成为这个this指代的对象就可以了,那么如何指定小明是这个函数的上下文呢？直接使用call()或apply()就可以指定，代码如下：

function sum() {
    console.log(this.chinese + this.math + this.english);
}
var xiaoming = {
    chinese: 80,
    math: 95,
    english: 93
};
sum.call(xiaoming);  // sum打点调用call方法，call方法传入xiaoming这个参数，即可将sum的上下文指定为xiaoming
sum.apply(xiaoming);  // 这里的apply同call方法

call() 和 apply() 的区别：

在函数需要传参的时候，call和apply在使用时就有区别了。比如上面的例子中，出了语文、数学、外语三门成绩外，还有两项额外的加分，这两项额外的加分，需要作为实参传入到sum()函数中。call和apply在使用时的区别如下：

function sum(b1, b2) {
    console.log(this.chinese + this.math + this.english + b1 + b2);
}
var xiaoming = {
    chinese: 80,
    math: 95,
    english: 93
};
sum.call(xiaoming, 5, 3);  // 实参加逗号罗列传入
sum.apply(xiaoming, [5, 3]);  // 实参通过数组的形式传入

上面代码的运行结果如下：

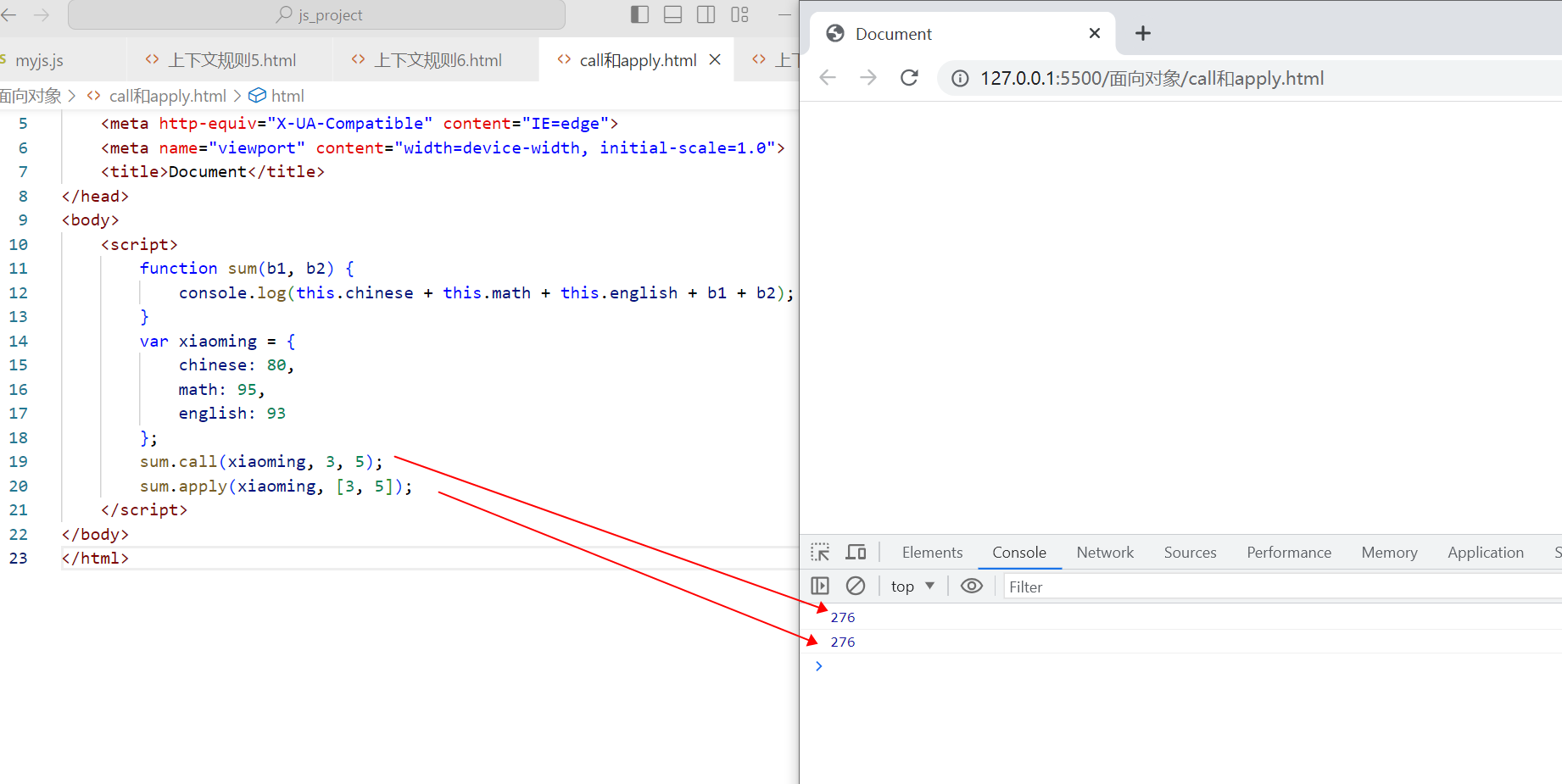
call() 和 apply() 的使用场景举例

什么情况下只能用其中之一呢？

比如下面的例子中，就只能用apply()，而不能用call()：

function fun1() {
    fun2.apply(this, arguments);
}
function fun2(a, b) {
    console.log(a + b);
}
fun1(33, 44)

⭐ 上下文规则总结

规则	上下文
对象.函数()	对象
函数()	window
数组[下标]()	数组
IIFE	window
定时器	window
DOM事件处理函数	绑定DOM的元素
call和apply	任意指定