1、介绍
该软件包致力于生成离散三维域的各向同性简化网格。要网格化的域是三维空间的子集,需要有界。域可以连接或由多个组件组成和/或细分为几个子域。
边界曲面和细分曲面是平滑曲面或分段平滑曲面,由平面或曲面面片形成。表面可能表现出一维特征(例如折痕边缘)和0维特征(例如,作为角尖端、尖端或飞镖的奇异点),这些特征必须在网格中相当近似。
输出网格是一个三维三角剖分,包括近似每个输入域特征的子网格:子域、边界曲面面片或维度为0或1的输入域特征。因此,输出网格包括覆盖每个子域的3D子网格、近似每个边界或细分曲面片的曲面网格、用于每个一维特征的折线近似,当然还有每个角上的顶点。
该软件包的主要入口点是两个分别生成和细化此类网格的全局函数。网格生成器经过定制,可以输出尽可能满足用户需求的网格,例如在尺寸字段方面或根据某些用户自定义的质量标准。
此网格生成器中使用的网格引擎基于 Delaunay 细化。它使用受限 Delaunay 三角剖分来近似一维曲线和曲面片。在细化之前,如果在任何一维特征上设置保护球的机制,以确保这些特征在网格中的公平表示,并保证细化过程的终止,无论输入几何形状如何,特别是无论边界和细分曲面片可能形成的小角度如何。在 Delaunay 细化之后是网格优化阶段,以去除碎片并提供高质量的网格。
可选地,网格化和优化算法支持多核共享内存架构,以利用可用的并行性。
1.1、输入域
假设要网格化的域是有界的,并且可以表示为纯3D复数。3D复数是一组具有0、1、2和3维的面,使得所有面都是成对不相交的,并且复数的每个面的边界是复数中低维面的并集。3D复数是纯的,这意味着每个面都包含在3维面中,因此复数完全由其3D面及其子面的集合描述。然而,3D复数不需要连接。具有小于或等于2维的面组成的集合形成了一个2D子复数,它不需要是流形,也不需要是纯的,也不需要是连接的:一些3D面在其边界面上可能有悬垂的2D或1D面。
在其余文档中,我们将输入三维复数称为输入域。输入域的表面维度为0、1、2和3,分别称为角、曲线、曲面片和子域,以明确区分它们与网格的表面,网格的表面称为顶点、边、面和单元。
请注意,输入的复杂面不需要是线性的,也不需要是平滑的。例如,曲面片可以是平滑的曲面片,也可以是具有边界的曲面网格的一部分。曲线可以是直线段、参数化曲线或多段线。这些特征中的每一个都会在最终网格中精确表示。
输入域的0和1维特征通常是子域边界的奇异点,但这不是必需的。此外,这些特征不需要覆盖所有子域边界奇点,而只需要覆盖那些需要在最终网格中准确表示的奇点。在下文中,我们说当域具有需要在网格中准确表示的0维和1维特征时,它具有特征,我们将这些特征称为暴露特征。因此,一个域可能没有特征,要么是因为所有边界曲面面片都是光滑的闭合曲面,要么只是因为连接不同曲面面片的曲线和这些面片的奇点不需要在最终网格中精确近似。
还要注意,输入复杂面不需要连接。输入域的面由索引标识。如果子域未连接,则其不同组件将接收相同的索引。同样,不同的曲面面片、曲线或角可以共享相同的索引。特征的每个连接组件都将在最终网格中准确表示。然而,请注意,输入复数中多重连接面的出现可能会影响网格生成器执行的内部拓扑检查的相关性。
域作为域类(通常称为oracle)传递给网格生成函数,该域类提供与域、子域、边界曲面面片以及0维和1维公开特征(如果有的话)相关的谓词和构造函数。主要是,oracle提供了一个谓词来测试给定的查询点是否属于域,并在肯定的情况下找到它所在的子域。域类还提供谓词和构造函数来测试查询线段与边界曲面面片的交点,并构造交点(如果有的话)。最后,如果输入域包括一维暴露特征,则域类提供了在这些特征上构造采样点的方法。
当前的实现提供了类来表示由隐函数等值面、多面体域和通过3D标记图像定义的域所限定的域。目前,一维特征可以被定义为线段和折线段。
1.2、输出网格
生成的网格作为加权Delaunay 3D三角剖分的子复合体输出,该类提供网格元素的各种迭代器。
3D三角剖分根据受限的Delaunay三角剖分范式提供子域、曲面片、曲线和角点的近似值。这意味着每个子域由其圆心位于域(或子域)内的四面体单元的并集近似。每个曲面片由其对偶Voronoi边与曲面片相交的Delaunay网格面片的并集近似。这样的网格面片在下文中称为曲面面片。一维暴露特征由网格边序列近似,而0维暴露特征由网格顶点表示。
可以使用函数facets_in_complex_3_to_triangle_mesh()将复杂体的面提取为FaceGraph。
1.3、Delaunay细化算法
网格生成算法主要是Delaunay细化过程。Delaunay细化之前有一个保护阶段,以确保一维特征(如果有的话)的准确表示,然后是优化阶段,以获得高质量的网格。
Delaunay细化过程由网格单元和表面小面的尺寸和形状相关的标准驱动。当没有违反标准的网格单元或表面小面时,细化过程终止。
这些标准旨在实现网格顶点的良好分布,同时确保细化过程的终止。这些标准可以根据用户需要进行调整,例如实现网格元素对尺寸字段的尊重,网格中边界表面表示的一些拓扑条件,和/或边界表面近似的一些误差界限。
在某种程度上,用户可以将Delaunay细化调整到网格质量和网格密度之间的规定权衡。网格密度是指网格顶点和单元的数量,即网格的复杂性。这里提到的网格质量是由表面面元端网格单元的半径边比来衡量的,其中单形(三角形或四面体)的半径边比是其外接圆半径与其最短边长度的比值。
1.4、0维和1维暴露特征的保护
如果域描述包含 0 维特征,则相应的点将从开始插入到 Delaunay 三角剖分中。
如果域具有一维暴露特征,则使用保护球的方法[7]、[8]来在网格中实现这些特征的精确表示,并保证无论由输入表面片形成的二面角是给定的1-特征还是由两个1-特征形成的0-特征,细化过程都会终止。
根据这种方法,一维特征被采样点采样,并被以采样点为中心的保护球覆盖,其方式是:
三个球没有相交;
没有一对球以不同的1-特征为中心相交。
嵌入网格的三角剖分实际上是一个加权Delaunay三角剖分,三角剖分通过插入所有保护球初始化,这些保护球被视为加权点。然后,如前所述启动Delaunay细化过程,不同的是细化点不再是圆心,而是加权圆心。细化过程插入的所有Steiner顶点都被赋予零权重。该方法保证:
连接一维特征上两个连续中心的每个片段将保留在三角测量中,从而确保一维特征的准确近似;
精炼过程将永远不会尝试在保护球的联合中插入精炼点,这确保了精炼过程的终止。
1.5、优化阶段
除了属于薄片家族的四面体之外,任何准退化的四面体都具有较大的半径边比。薄片很容易获得,因为它是4个接近3D球赤道圆的点的凸包,并且沿着这个圆大致均匀分布。 Delaunay细化跟踪具有较大半径边比的四面体,因此消除了除薄片之外的各种形状不佳的四面体。
因此,在细化过程结束时,网格中可能仍存在一些条形四面体。优化阶段旨在消除这些条形四面体。
优化阶段是一系列优化过程,其中包括以下可用的优化器:ODT平滑器、Lloyd平滑器、条纹扰动器和条纹挤压器。
Lloyd和ODT平滑器是全局优化器,它们将网格顶点移动到最小化网格能量的位置。在这两种情况下,网格能量是由分段线性函数对函数f(x)=x2进行插值而产生的L1误差。在Lloyd平滑器的情况下,插值在网格顶点集的每个Voronoi单元中都是线性的。在ODT平滑器的情况下,插值在网格顶点的Delaunay三角剖分的每个单元中都是线性的,因此ODT是优化Delaunay三角剖分的缩写。
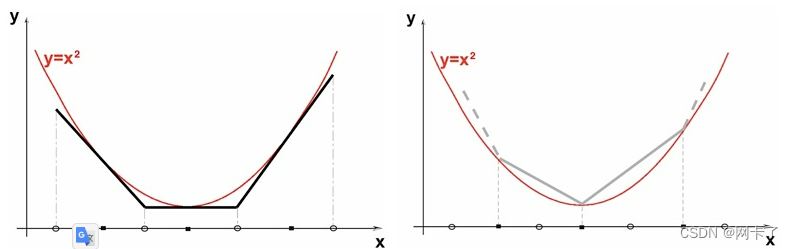
ODT(左)和Lloyd(右)平滑器最小化网格能量的一维图示。
众所周知,劳埃德优化器对网格中出现的碎片视而不见,而ODT平滑器倾向于将它们赶出去。它们都是全局优化器,这意味着它们试图改善整个网格,而不是专注于最糟糕的元素。然而,根据经验,两者都是非常有效的优化初步步骤,因为它们倾向于提高扰动器和/或之后应用的挤出器的效率,见下图。
扰动器和挤出器专注于改善最差的网格元素。扰动器通过局部改变顶点位置来改善网格,旨在使碎片消失。挤出器通过用最优权重重新加权网格顶点来追踪剩余的碎片。
每个优化过程都可以根据用户要求和可用时间进行激活或不激活和调整。默认情况下,只有扰动器和挤出器被激活。
优化过程旨在提高网格质量。但是,请注意,这种改进是通过扰动网格顶点和修改网格连接性来实现的,这会影响对细化标准的严格遵守。虽然在Delaunay细化结束时可以严格遵守网格标准,但在某些优化过程之后,这可能不再成立。还要注意,默认行为确实涉及一些优化过程。
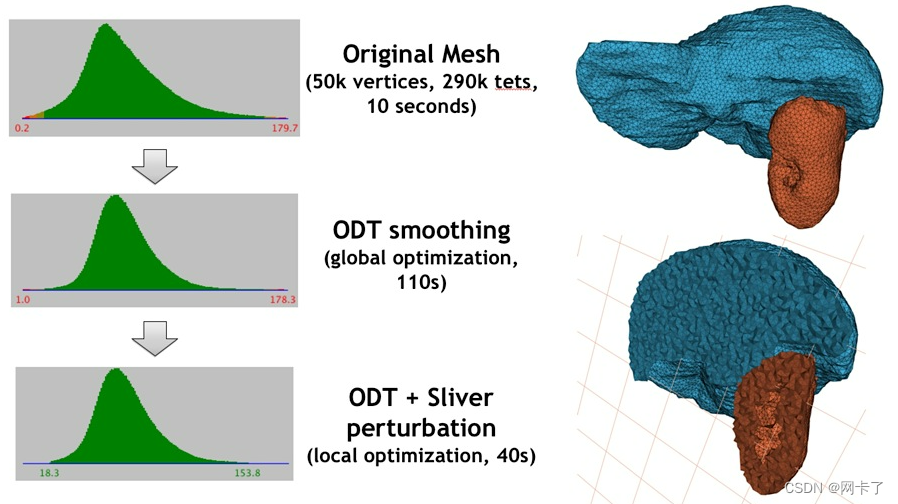
比较了全局优化器和扰动器的效果。左侧部分显示了Delaunay细化后(顶部)、一些ODT平滑后(中间)和扰动后(底部)网格单元的二面角分布。直方图下的数字给出了网格中最小和最大二面角的度数。
1.6、后期处理
此软件包提供的由Delaunay细化生成的四面体网格生成算法并不能保证输出网格的所有顶点都实际存在于最终网格中。
在大多数情况下,所有点都被使用,但是如果对象的几何形状与单形(三角形和四面体)的大小相比具有小的特征,则可能在限制的Delaunay三角剖分中选择的Delaunay面会错过三角剖分的一些顶点。四面体网格生成算法的并发版本还插入了一小部分辅助顶点,这些顶点属于三角剖分,但在网格化过程结束时与复杂网格隔离开来。
这些所谓的孤立顶点属于三角剖分,但不属于 C3T3 的任何单元。可以使用函数 remove_isolated_vertices() 将其删除。
2、接口
从CGAL 5.6开始,此包使用命名参数来设置参数
2.1、全局函数
通过调用以下两个函数之一启动三维网格生成过程:
template <class C3T3, class MeshDomain, class MeshCriteria, class NamedParameters>
C3T3 make_mesh_3(const MeshDomain& domain,
const MeshCriteria& criteria,
const NamedParameters& np);
template <class C3T3, class MeshDomain, class MeshCriteria, class NamedParameters>
void refine_mesh_3(C3T3& c3t3,
const MeshDomain& domain,
const MeshCriteria& criteria,
const NamedParameters& np);函数 make_mesh_3() 从头开始生成输入域的网格,而函数 refine_mesh_3() 细化输入域的现有网格。请注意,由于对 0 和 1 维特征的保护不依赖于 Delaunay 细化,函数 refine_mesh_3() 没有保留特征的参数。
以下部分描述了这两个全局函数的不同模板参数(及其要求)。
2.2、数据结构
模板参数C3T3需要是概念MeshComplex_3InTriangulation_3的模型,这是一种数据结构,用于表示嵌入在3D三角剖分中的三维复杂体。在这两个函数中,C3T3类型的实例用于维护当前的近似单形网格,并在过程结束时表示最终的3D网格。
嵌套 3D 三角剖分需要由类模板 CGAL::Mesh_triangulation_3 提供的嵌套类型CGAL::Mesh_triangulation_3::type。该三角剖分的类型是围绕类CGAL::Regular_triangulation_3 的包装,其顶点和单元基类分别是 MeshVertexBase_3 和 MeshCellBase_3 概念的模型。
2.3、领域Oracle及其特征参数
MeshDomain_3定义了用于生成三维网格的几何体。它通常由一组点、线、面或体组成,这些元素定义了要生成的网格的形状和大小。MeshDomain_3可以由各种类型的的数据源生成,例如STL文件、medit文件、avizo文件等。
使用MeshDomain_3,可以定义各种形状的三维网格,例如四面体网格、六面体网格、金字塔网格等。它还支持对网格进行细化或粗化,以生成不同精细程度的网格。
模板参数 MeshDomain 需要是概念 MeshDomain_3 的模型。类型 MeshDomain 的参数域是网格生成算法已知的唯一链接,通过该链接可以知道要离散化的域。
这个概念提供了成员函数,用于测试查询段是否与边界曲面相交,并在肯定的情况下计算交点。 MeshDomain_3 概念添加了成员函数,这些函数给定一个查询点,可以判断该点是位于域内还是域外,如果位于域内,还可以判断该点位于哪个子域内。
如果域描述包含必须在最终网格中准确表示的 0 维和 1 维特征,则模板参数 MeshDomain 需要是概念 MeshDomainWithFeatures_3 的模型。概念 MeshDomainWithFeatures_3 主要提供 0、1 和 2 维特征的关联图,以及在曲线上构造采样点的成员函数。
域为 MeshDomainWithFeatures_3 模型的用户可以选择是否在网格中显示域的角和曲线,使用以下参数:
parameters::features(domain) 根据域设置特征,即如果域是 MeshDomainWithFeatures_3,则考虑 0 和 1 维特征。
parameters::no_features() 阻止网格中 0 和 1 维特征的表示。这对于获得具有特征的域的平滑和粗糙近似很有用。
2.4、网格划分标准
模板参数 MeshCriteria 必须是概念 MeshCriteria_3 的模型,或者如果域具有公开的特征,则必须是细化概念 MeshCriteriaWithFeatures_3 的模型。传递给网格生成器的 MeshCriteria 类型的参数指定了网格中四面体和边界曲面网格中三角形的尺寸和形状要求。这些条件是驱动细化过程的规则的条件。在细化过程结束时,网格元素满足这些条件。请注意,在优化阶段之后,这可能不再严格成立,但最后这个阶段的设计只是为了提高网格质量。
表面刻面的标准由以下四个参数决定:必须掌握
facet_angle。该参数控制曲面小面的形状。具体来说,它是曲面小面角度(以度为单位)的下限。当边界曲面光滑时,如果该角度限制最大为30度,则可以保证网格化过程的终止。
facet_size。该参数控制曲面小面的大小。每个曲面小面都有一个曲面Delaunay球,该球是围绕曲面小面并以曲面片为中心的球。参数facet_size是一个常数或空间可变标量场,为曲面Delaunay球的半径提供上限。
facet_distance。此参数控制边界和细分曲面的近似误差。具体而言,它是一个常数或空间变量标量场。它为曲面分面的圆心与此分面的曲面Delaunay球的中心之间的距离提供了上限。
facet_topology。此参数控制着每个曲面面必须验证的拓扑约束集。默认情况下,曲面面的每个顶点必须位于曲面片、曲线或角上。它也可以设置为检查曲面面的三个顶点是否属于同一曲面片。这必须谨慎进行,因为这样的标准需要输入曲面片的每个交点都是输入的一维特征。
网格单元的标准由两个参数控制:
cell_radius_edge_ratio。此参数控制网格单元的形状(但不能过滤碎片,如前所述)。它是网格四面体的外接圆半径与其最短边之间的比率的上限。此参数有一个理论界限:当cell_radius_edge_ratio大于2时,Delaunay细化过程保证终止。
cell_size。该参数控制网格四面体的大小。它是一个标量或空间可变标量场。它提供了网格四面体外接圆半径的上限。
下图显示了网格生成过程对这些参数的反应。
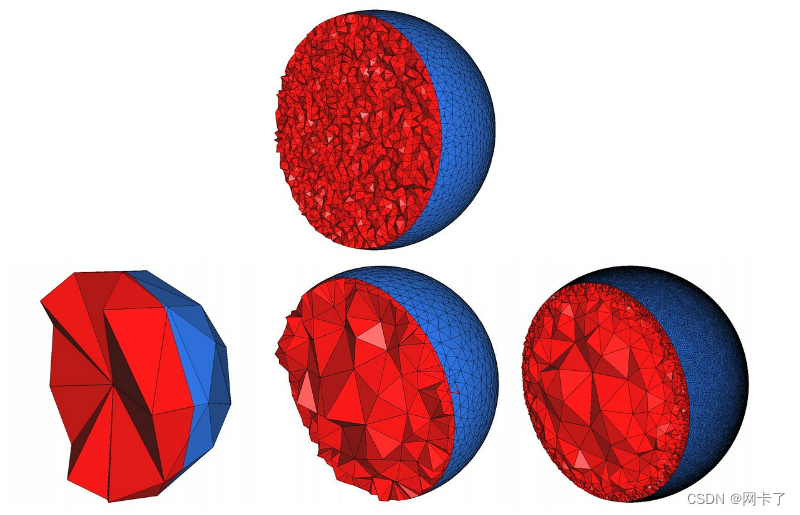
顶部:使用表面面的角度范围、半径范围和距离范围的参数(25,0.15,0.05)以及网格单元的半径边界和半径范围的参数(4,0.2)来获得网格。结果是一个包含大约相同大小的四面体的均匀网格。
左下:通过放宽四面体和面的尺寸范围来获得网格。结果是一个小的粗糙网格。
中间底部:通过将表面面的距离范围收紧到0.01,从之前的网格中获得网格。结果是一个分级的三维网格,表面网格密集,达到精确近似。
右下:通过将表面面的半径范围固定到0.01,从之前的网格中获得网格。然后表面网格更密集,达到尺寸范围。
如果域具有一维暴露特征,则标准包括一个尺寸字段,用于指导使用保护球中心对一维特征进行采样。
edge_size。这个常数或变量标量字段用作1-特征上连续的两个保护球中心之间距离的上限。使用1维特征保护时,该参数必须设置为正值。
2.5、优化参数
四个附加参数是优化参数。它们控制执行哪些优化过程,并允许用户调整已激活的优化过程的参数。这些参数具有内部类型,未作描述,但库提供了全局函数来生成这些类型的适当值:
parameters::lloyd() 和 parameters::no_lloyd() 激活和停用 Lloyd 平滑器。
parameters::odt()和parameters::no_odt()用于激活和停用ODT平滑器。
parameters::perturb() 和 parameters::no_perturb() 激活和停用扰动器。
parameters::exude()和parameters::no_exude()用于激活和停用挤出机。
这些参数是可选的,可以按任何顺序传递。如果未传递一个参数,则使用默认值。默认情况下,只有扰动器和挤出器被激活。请注意,无论是由 make_mesh_3() 或 refine_mesh_3() 激活的优化过程是什么,它们总是按照以下子顺序的顺序启动:ODT-smoother、Lloyd-smoother、perturber 和 exuder。
该软件包还提供了四个全局函数,可以独立启动每个优化过程。这些函数对于每种优化方法的效率的高级实验非常有用。但是请注意,挤出机增加了由顶点位置决定的网格顶点权重。因此,挤出过程绝不能在平滑器或扰动器之前运行。为了达到最大效率,无论激活了哪种优化过程,都应该按照以下顺序启动:ODT-平滑器、Lloyd-平滑器、扰动器和挤出机。
template< class C3T3, class MeshDomain >
Mesh_optimization_return_code lloyd_optimize_mesh_3(C3T3& c3t3, const MeshDomain& domain);
template< class C3T3, class MeshDomain >
Mesh_optimization_return_code odt_optimize_mesh_3(C3T3& c3t3, const MeshDomain& domain);
template< class C3T3, class MeshDomain >
Mesh_optimization_return_code perturb_mesh_3(C3T3& c3t3, const MeshDomain& domain);
template< class C3T3 >
Mesh_optimization_return_code exude_mesh_3(C3T3& c3t3);请注意,激活优化过程或启动这些过程的全局函数本身具有参数,以调整优化过程。
2.6、并行计算
CGAL::Mesh_triangulation_3 提供了一些成员函数和类型,用于处理三维三角剖分。其中一些重要的成员函数包括:create_triangulation_data_structure():创建一个用于存储三角剖分数据的数据结构。insert_in_complex():将一个点或一个线段插入到三角剖分中。extract_complex():从三角剖分中提取一个复杂体(即一组相互连接的三角形)。refine():细化三角剖分,以改善网格质量。
在定义三角剖分类型时,通过将Mesh_triangulation_3类的第三个模板参数设置为parallel_tag来实现并行网格划分和优化算法。请注意,当用户提供他/她自己的顶点和单元基类时,MeshVertexBase_3和MeshCellBase_3概念会带来额外的要求。
并行算法要求可执行文件链接到英特尔TBB库。为了控制使用的线程数,用户可以使用tbb::task_scheduler_init类。有关更多详细信息,请参阅TBB文档。
3、输入输出
支持多种文件格式用于编写网格:
Medit 文件格式,使用CGAL::IO::write_MEDIT()。
VTK(VTU / VTP)文件格式,使用CGAL::IO::output_to_vtu()。
Avizo文件格式,使用CGAL::IO::output_to_avizo()。
使用 CGAL::IO::output_to_tetgen()的Tetgen文件格式。
4、性能
我们在这里提供了网格生成算法性能的一些基准。
4.1、Delaunay细化算法
我们对半径为1的分析球体进行网格划分。
| Size bound | vertices nb | facets nb | tetrahedra nb | CPU Time (s) | vertices/second |
| 0.2 | 499 | 488 | 2,299 | 0.0240 | 20,800 |
| 0.1 | 3,480 | 2,046 | 18,756 | 0.146 | 23,800 |
| 0.05 | 25,556 | 8,274 | 149,703 | 1.50 | 17,000 |
| 0.025 | 195,506 | 33,212 | 1,194,727 | 17.4 | 11,200 |
| 0.0125 | 1,528,636 | 134,810 | 9,547,772 | 179 | 8,530 |
我们对一个由大约50000个顶点和100000个三角形组成的闭合三角形曲面界定的体积进行网格划分。下图显示了当尺寸设置为0.005时获得的网格。

| Size bound | vertices nb | facets nb | tetrahedra nb | CPU Time (s) | vertices/second |
| 0.04 | 423 | 717 | 1,332 | 0.488 | 866 |
| 0.02 | 2,638 | 3,414 | 10,957 | 2.64 | 998 |
| 0.01 | 18,168 | 15,576 | 90,338 | 13.9 | 1,310 |
| 0.005 | 129,442 | 64,645 | 722,018 | 66.7 | 1,940 |
| 0.0025 | 967,402 | 263,720 | 5,756,491 | 348 | 2,780 |
我们对2号图像进行网格划分。此图像的大小为512x512x172体素(约45M体素)。体素的大小为0.78mm x 0.78mm x 1.6mm。下图显示了将大小设置为4时获得的网格。

| Size bound (mm) | vertices nb | facets nb | tetrahedra nb | CPU Time (s) | vertices/second |
| 16 | 3,898 | 4,099 | 20,692 | 0.344 | 11,300 |
| 8 | 34,117 | 27,792 | 199,864 | 3.09 | 11,000 |
| 4 | 206,566 | 86,180 | 1,253,694 | 22.4 | 9,230 |
| 2 | 1,546,196 | 329,758 | 9,617,278 | 199 | 7,780 |
4.2、并行性能
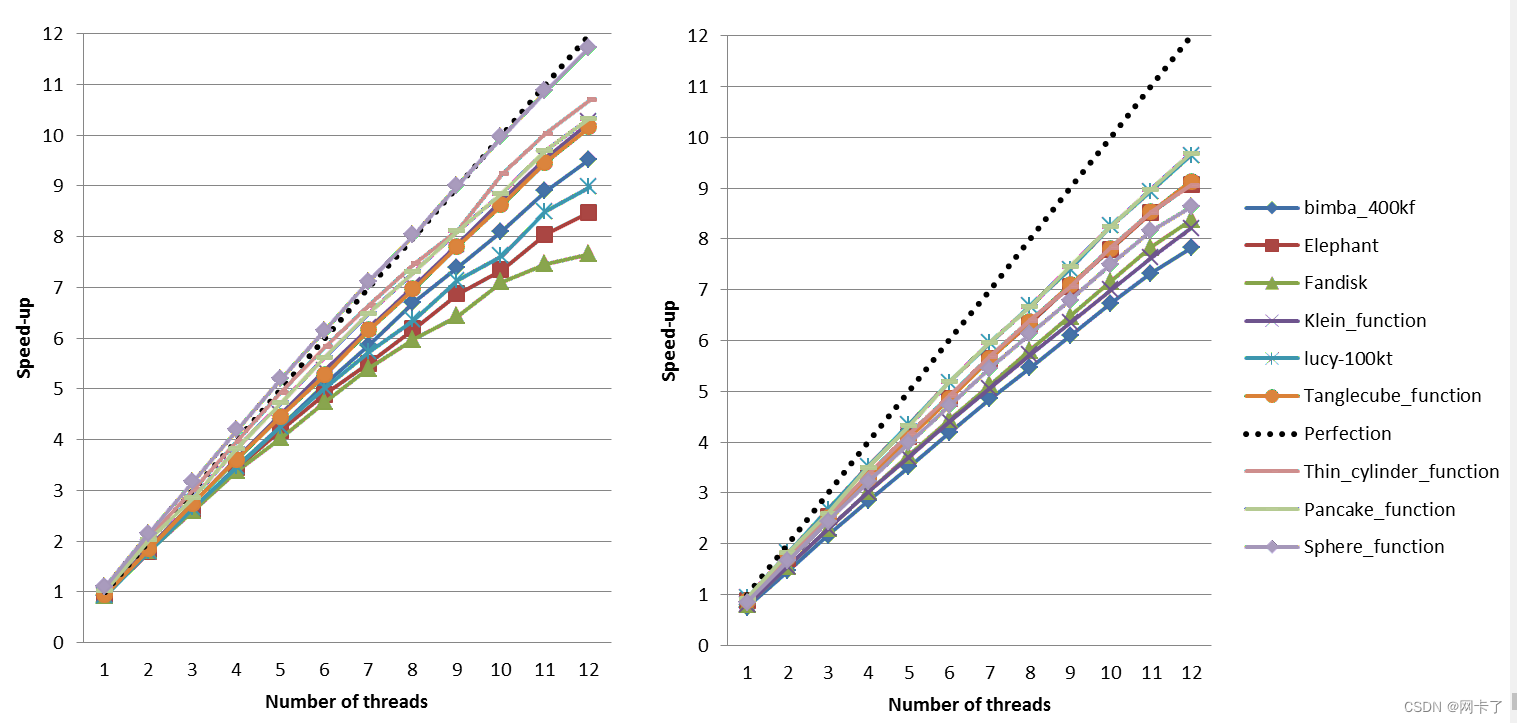
与顺序版本的算法相比,面细化加速(左)和单元细化加速(右)。
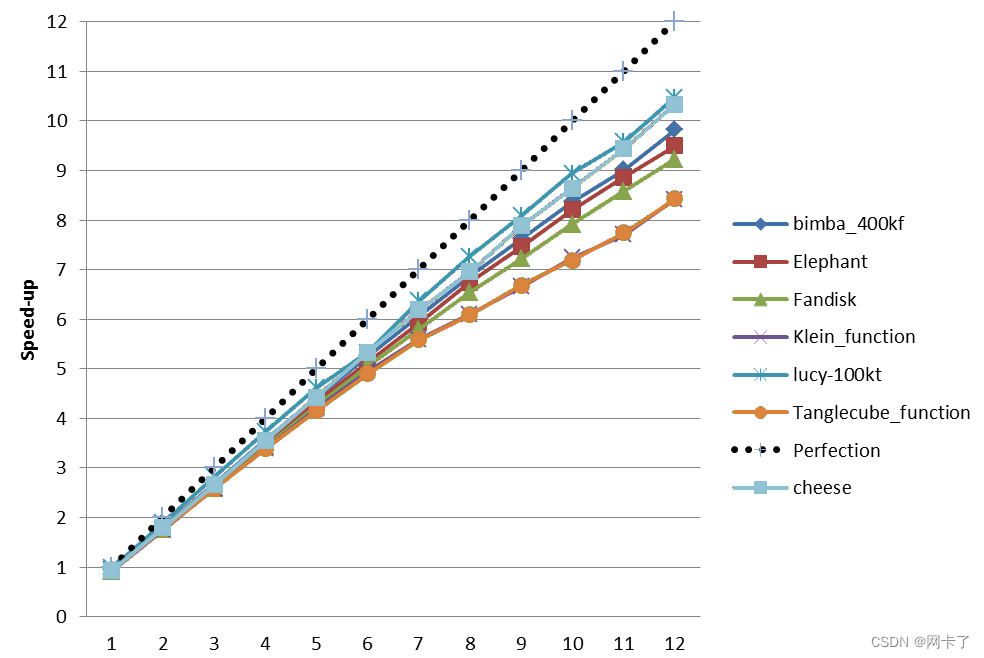
与顺序版本的算法相比,Lloyd优化加快了速度。并行ODT表现出类似的性能。
CGAL 5.6 - 3D Mesh Generation: User Manual