传送门：AtCoder Beginner Contest 332 - AtCoder

a,b,c都还是很基础了。d题是一个bfs的纯暴力问题。

E - Lucky bag

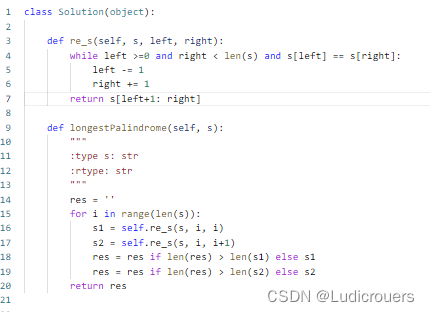
看看范围，n==15，第一个想法是dfs纯暴力，但所有的情况太大，各种决策层出不穷，会t。所以转而想到了状压dp，我们可以通过状压的迭代省去很多麻烦，但是也止步于想到状压了，不是很会实现。其实这题是通过状压的表示来实现每个背包的状态。我觉得这是道很好的题。时间复杂度是

代码如下：

// #pragma GCC optimize(3)  //O2优化开启
#include<bits/stdc++.h>
using namespace std;
// #define int long long
typedef long long ll;
typedef pair<int,int> PII;
const int N=998244353;
// const int MX=0x3f3f3f3f3f3f3f3f; 
int n,m;

double b[25];
double sum[1<<15];
void icealsoheat(){
    cin>>n>>m;
    double avr=0;
    vector<double>dp(1<<15,1e30);
    for(int i=0;i<n;i++){
        cin>>b[i];
        avr+=b[i];
    }
    avr=avr/m;
    double ans=20000000;
    for(int i=0;i<(1<<n);i++){
        for(int j=0;j<n;j++){
            if((i>>j)&1){
                sum[i]+=b[j];
            }
        }
        sum[i]=(avr-sum[i])*(avr-sum[i]);
    }
    // dp[0]=200000000;
    dp[0]=0;
    for(int i=0;i<m;i++){
        vector<double>ndp(1<<15,1e30);
        for(int j=0;j<(1<<n);j++){
            for(int t=j;;t=(t-1)&j){
                ndp[j]=min(ndp[j],dp[t]+sum[t^j]);
                if(t==0)break;
            }
        }
        dp=ndp;
    }
    printf("%.10lf",dp[(1<<n)-1]/m);
}
signed main(){
    ios::sync_with_stdio(false);
    cin.tie();
    cout.tie();
    int _yq;
    _yq=1;
    // cin>>_yq;
    while(_yq--){
        icealsoheat();
    }
}

F - Random Update Query

这题一看就是个线段树，最近一直在练线段树，终于可以小试牛刀了。我们只需要用俩标记去维护区间中的累乘以及累加，代码如下：

// #pragma GCC optimize(3)  //O2优化开启
#include<bits/stdc++.h>
using namespace std;
#define int long long
typedef long long ll;
typedef pair<int,int> PII;
const int mod=998244353;
const int MX=0x3f3f3f3f3f3f3f3f; 
int b[200005];
int n,m;
int kuai(int a,int b){
    int ans=1;
    while(b){
        if(b&1)ans=ans*a%mod;
        b>>=1;
        a=a*a%mod;
    }
    return ans%mod;
}

struct we{
    int l,r;
    int s,p;
    #define ls i*2
    #define rs i*2+1
}tr[4000005];

void pushdow(int i){
    if(tr[i].s||tr[i].p!=1){
        tr[ls].s=(tr[ls].s*tr[i].p+tr[i].s)%mod;
        tr[ls].p=tr[i].p*tr[ls].p%mod;
        tr[rs].s=(tr[rs].s*tr[i].p+tr[i].s)%mod;
        tr[rs].p=tr[i].p*tr[rs].p%mod;       
        tr[i].s=0;
        tr[i].p=1; 
    }
}

void build(int i,int l,int r){
    tr[i]={l,r,0,1};
    if(l==r){
        return;
    }
    int mid=(l+r)>>1;
    build(ls,l,mid);
    build(rs,mid+1,r);
}

void change(int i,int l,int r,int sx,int px,int fx){
    if(tr[i].l>=l&&tr[i].r<=r){
        tr[i].p=tr[i].p*px%mod;
        tr[i].s=(tr[i].s*px%mod+sx*fx%mod)%mod;
        return;
    }
    pushdow(i);
    int mid=(tr[i].l+tr[i].r)>>1;
    if(l<=mid)change(ls,l,r,sx,px,fx);
    if(r>mid)change(rs,l,r,sx,px,fx);

}

int query(int i,int l,int r){
    if(tr[i].l==tr[i].r){
        return (tr[i].p*b[l]%mod+tr[i].s)%mod;
    }
    pushdow(i);
    int mid=(tr[i].l+tr[i].r)>>1;
    if(r<=mid)return query(ls,l,r);
    else return query(rs,l,r); 

}


void icealsoheat(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>b[i];
    }
    build(1,1,n);
    while(m--){
        int l,r,x;
        cin>>l>>r>>x;
        int fx=kuai(r-l+1,mod-2)%mod;
        int px=(r-l)*kuai(r-l+1,mod-2)%mod;
        change(1,l,r,x,px,fx);
    }
    for(int i=1;i<=n;i++){
        cout<<query(1,i,i)<<" ";
        // cout<<"***\n";
    }
}
signed main(){
    ios::sync_with_stdio(false);
    cin.tie();
    cout.tie();
    int _yq;
    _yq=1;
    // cin>>_yq;
    while(_yq--){
        icealsoheat();
    }
}