介绍
最短路径:从起点开始访问所有的路径,到达终点的路径有多条,其中路径的权值最短的一条则为最短路径。
最短路径算法有深度优先遍历、广度优先遍历、Bellman-Ford算法、弗洛伊德算法、SPFA算法、迪杰斯特拉算法等。
而本篇讲的是利用深度优先遍历(DSF)求最短路径。
深度优先遍历(DSF)
先来看下面的例子,起点为A,终点为E。
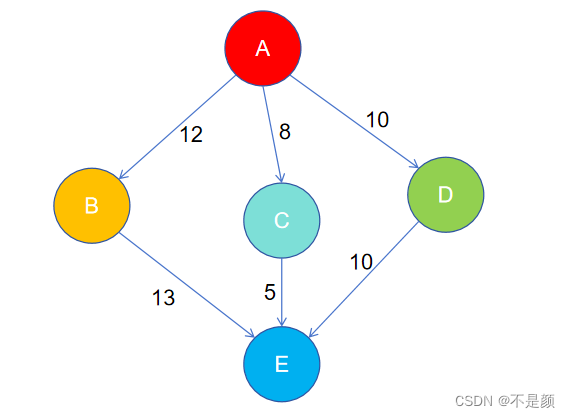
A-C-E 路径是最短的,权值为13。
首先从 A 出发,有三个分支,先选择一个分支D,将D设置为访问过的状态(避免重复访问),同时保存路径D,从D出发有一个分支E,将E设置为访问过的状态,保存路径E,到达E,E为终点,所以找到了一条可行路径,将它的权值和最小权值比较,如果小于就更新最小权值,同时有一个数组保存最短路径,将这条可行路径拷贝到数组里。
然后沿路返回将E、D设置为未被访问的状态,同时在路径中删除E、D,回到起点A选择分支C,将C设为访问过的状态并且保存C,C有一个分支E,将E设为访问过的状态并且保存,此时E为终点,找到一条可行路径,将它的权值和最小权值比较,如果小于就更新最小权值,同时有一个数组保存最短路径,将这条可行路径拷贝到数组里。
……
主要用到了递归的思想。
核心代码部分
int min_weight = 0x7FFFFFFF; //最短路径的权重
int min_path[MaxSize] = { 0 };// 最短的路径
int steps; //已走过的步数
int path[MaxSize] = { 0 }; //保存当前走的这条路径
/*深度遍历求解从起点到终点的最短路径*/
void DFS(AdjListGraph& G, int start,int end,int weights) //weights是前面已走的路径累计的权重
{
visited[start] = true; //访问状态设为true
if (start == end) //如果起点就是终点,递归结束
{
for (int i = 0; i < steps; i++)
{
cout << G.adjlist[path[i]].date << " "; //打印一条可行的路径
}
cout << "该路径的长度为:" << weights << endl;
if (min_weight > weights) //找到了一条更短的路径,更新最短路径
{
min_weight = weights;
memcpy(min_path, path, steps * sizeof(int));
}
}
EdgeNode* tmp = G.adjlist[start].first;
int weight = 0; //下一个要访问的节点的权重
int cur = -1;//下一个要访问的节点的位置
while (tmp)
{
cur = tmp->adjvex;
weight = tmp->weight;
if (visited[cur] == false)
{
visited[cur] = true;
path[steps++] = cur; //保存路径
DFS(G, cur, end, weights + weight);
visited[cur] = false; //还原状态
path[--steps] = 0;
}
tmp = tmp->next;
}
}建议先看递归未结束的代码。
所有的代码以及测试样例
#include <iostream>
#include <queue>
using namespace std;
//利用深度优先遍历求最短路径算法
#define MaxSize 1024
typedef char DateElem;
//边
typedef struct _EdgeNode
{
int adjvex; //与之相邻的节点在数组中的位置
int weight; //边的权重
struct _EdgeNode* next; //指向下一条相邻的边
}EdgeNode;
//顶点
typedef struct _VertexNode
{
DateElem date; //顶点的数据
struct _EdgeNode* first; //指向第一条与之相邻的边
}VertexNode, AdjList;
//邻接链表
typedef struct _AdjListGraph
{
AdjList* adjlist; //数组,保存着所有的顶点
int vex; //顶点数
int edge; //边数
}AdjListGraph;
bool visited[MaxSize]; //节点是否被访问过,被访问过设为true
//图的初始化
void Init(AdjListGraph& G)
{
G.adjlist = new AdjList[MaxSize];
G.edge = 0;
G.vex = 0;
for (int i = 0; i < MaxSize; i++)
{
visited[i] = false;
}
}
int Location(AdjListGraph& G, DateElem c);
//图的创建
void Create(AdjListGraph& G)
{
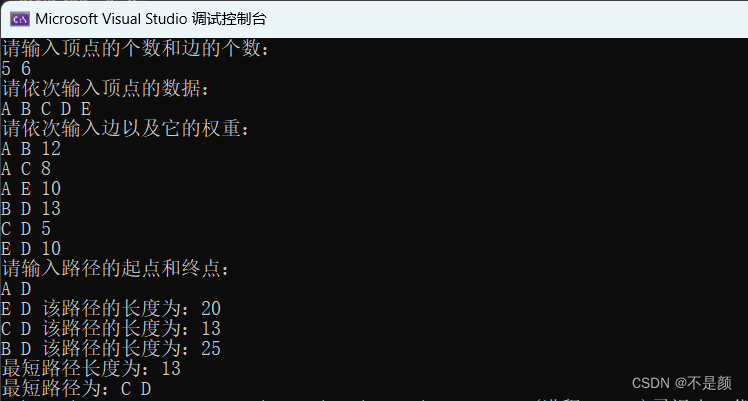
cout << "请输入顶点的个数和边的个数:" << endl;
cin >> G.vex >> G.edge;
cout << "请依次输入顶点的数据:" << endl;
for (int i = 0; i < G.vex; i++)
{
cin >> G.adjlist[i].date;
G.adjlist[i].first = NULL;
}
cout << "请依次输入边以及它的权重:" << endl;
DateElem v1, v2;
int weight = 0;
int i1 = 0, i2 = 0;
for (int i = 0; i < G.edge; i++)
{
cin >> v1 >> v2;
cin >> weight;
i1 = Location(G, v1);
i2 = Location(G, v2);
if (i1 != -1 && i2 != -1) //确保两个顶点存在
{
EdgeNode* tmp = new EdgeNode;
tmp->adjvex = i2;
tmp->weight = weight;
tmp->next = G.adjlist[i1].first; //头插
G.adjlist[i1].first = tmp;
}
}
}
/*通过顶点保存的数据找到顶点在图中的位置*/
int Location(AdjListGraph& G, DateElem c)
{
for (int i = 0; i < G.vex; i++)
{
if (G.adjlist[i].date == c)
{
return i;
}
}
return -1; //没找到
}
int min_weight = 0x7FFFFFFF; //最短路径的权重,初始化为int类型中最大的整数
int steps; //已走过的步数
int path[MaxSize] = { 0 }; //保存当前走的这条路径
int min_path[MaxSize] = { 0 };// 最短的路径
/*深度遍历求解从起点到终点的最短路径*/
void DFS(AdjListGraph& G, int start,int end,int weights) //weights是前面的路径累计的权重
{
visited[start] = true; //访问设为true
if (start == end) //如果起点就是终点
{
for (int i = 0; i < steps; i++)
{
cout << G.adjlist[path[i]].date << " "; //一条可能的路径
}
cout << "该路径的长度为:" << weights << endl;
if (min_weight > weights) //找到了一条更短的路径,更新最短路径
{
min_weight = weights;
memcpy(min_path, path, steps * sizeof(int));
}
}
EdgeNode* tmp = G.adjlist[start].first;
int weight = 0; //下一个要访问的节点的权重
int cur = -1;//下一个要访问的节点的位置
while (tmp)
{
cur = tmp->adjvex;
weight = tmp->weight;
if (visited[cur] == false)
{
visited[cur] = true;
path[steps++] = cur;
DFS(G, cur, end, weights + weight);
visited[cur] = false; //上一个路线的顶点设为未被访问的状态
path[--steps] = 0;
}
tmp = tmp->next;
}
}
int main(void)
{
AdjListGraph G;
//图的初始化
Init(G);
//图的创建
Create(G);
/* A B 12
A C 8
A E 10
B D 13
C D 5
E D 10 */
DateElem start, end;
cout << "请输入路径的起点和终点:" << endl;
cin >> start >> end;
DFS(G, Location(G, start), Location(G, end), 0);
cout << "最短路径长度为:" << min_weight << endl;
int i = 0;
cout << "最短路径为:";
while (i < MaxSize && min_path[i] != 0)
{
cout << G.adjlist[min_path[i]].date << " ";
i++;
}
return 0;
}