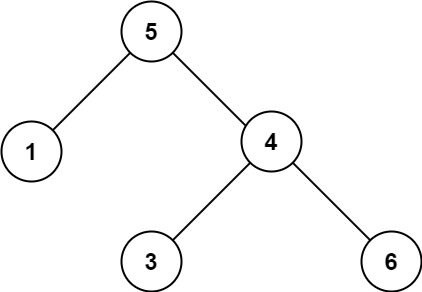
树的重心

• 无向图: 边没有方向 有向图:边有方向 只能单向询问

  • 无向图建立双向的边

  • 要求输出每种情况连通块个数最大值的最小值**(最小的最大值)**

  • 

  •   #include <cstdio>
      #include <cstring>
      #include <iostream>
      #include <algorithm>
      using namespace std;
      
      const int N=100010, M=N*2;
      
      int n;
      //类似拉链法 的存储方式
      int h[N], e[M], ne[M], idx;  
      //h[N]为n条以1~n为头节点的单链表  
      //e[N]为节点数值(编号)
      //ne[N]为指针
      int ans = N;  //ans为最终结果 因为要取最小的最大值 所以ans初始为最大值
      bool st[N];  //判断是否遍历过 
      
      void add(int a, int b)
      {
          e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
          //拉链法
      }
      
      int dfs(int u)
      {
          st[u] = true;  //标记遍历过 防止下一层时往回递归 死循环
          
          int size=0,sum=1;  //初始化 最大子树大小size 当前节点为根节点的整棵树大小sum
          for(int i=h[u];i!=-1;i = ne[i])
          {
              int j = e[i];
              if(st[j]) continue;  //j如果没被遍历过 才执行
              int s = dfs(j);  //递归找子树大小
              sum+=s;  //求所有子树大小和 再向上返回
              size = max(s,size);  //找最大子树大小
          }
           
          size = max(size, n - sum);  //因为从整棵树的根节点开始遍历 当前节点向上一定为一整个连通块 有了下面的最大子树大小 再求上面的连通块大小比较
          ans = min(ans,size);
          
          return sum;
      }
      
      int main(){
          cin>>n;
          
          memset(h, -1, sizeof h);  //初始化
          
          for (int i = 0; i < n - 1; i ++ ){
              int a,b;
              cin>>a>>b;
              add(a,b),add(b,a);  //建立双向边
          }
          
          dfs(1);  //从根节点开始
          
          cout<<ans<<endl;
          
          return 0;
      }