Leetcode 46 全排列

news2024/11/23 3:02:17

题意理解：

首先明确全排列是什么？使用集合里所有的元素，使用不同的顺序进行排列，所有的排列集合即为全排列。

        输入：nums = [1,2,3]

        输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

这里的元素不会重复，所以不需要去重。

解题思路：

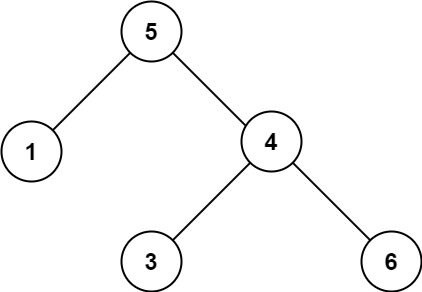
全排列也可用回溯的方式来解决，所以可以将其抽象为一棵树。

所有的结果在叶子节点收集。

其中与组合不同的是[1,2][2,1]是不同的，startIndex的使用在组合中是为了防止取到重复元素，但是排序可以取之前用过的元素，所以startIndex在此时不被需要。

        我们采用used来记录访问状态，保证元素每个仅取一次即可。

1.暴力回溯+剪枝优化

回溯三个关键要素：

确定返回值和参数列表

确定终止条件：path.size==nums.size,所有元素都用了一遍，即为一个排列结果

单层递归逻辑：控制每个元素仅用一次

List<List<Integer>> result=new ArrayList<>();
    LinkedList<Integer> path=new LinkedList<>();
    boolean[] used=null;
    public List<List<Integer>> permute(int[] nums) {
        used=new boolean[nums.length];
        backtracking(nums);
        return result;
    }
    public void backtracking(int[] nums){
        //终止条件
        if(path.size()==nums.length){
            result.add(new ArrayList<>(path));
            return;
        }
        //单层逻辑
        for(int i=0;i<nums.length;i++){
            //用过的数字剪枝——树枝去重
            if(used[i]==true) continue;
            path.add(nums[i]);
            used[i]=true;
            backtracking(nums);
            path.removeLast();
            used[i]=false;
        }
    }