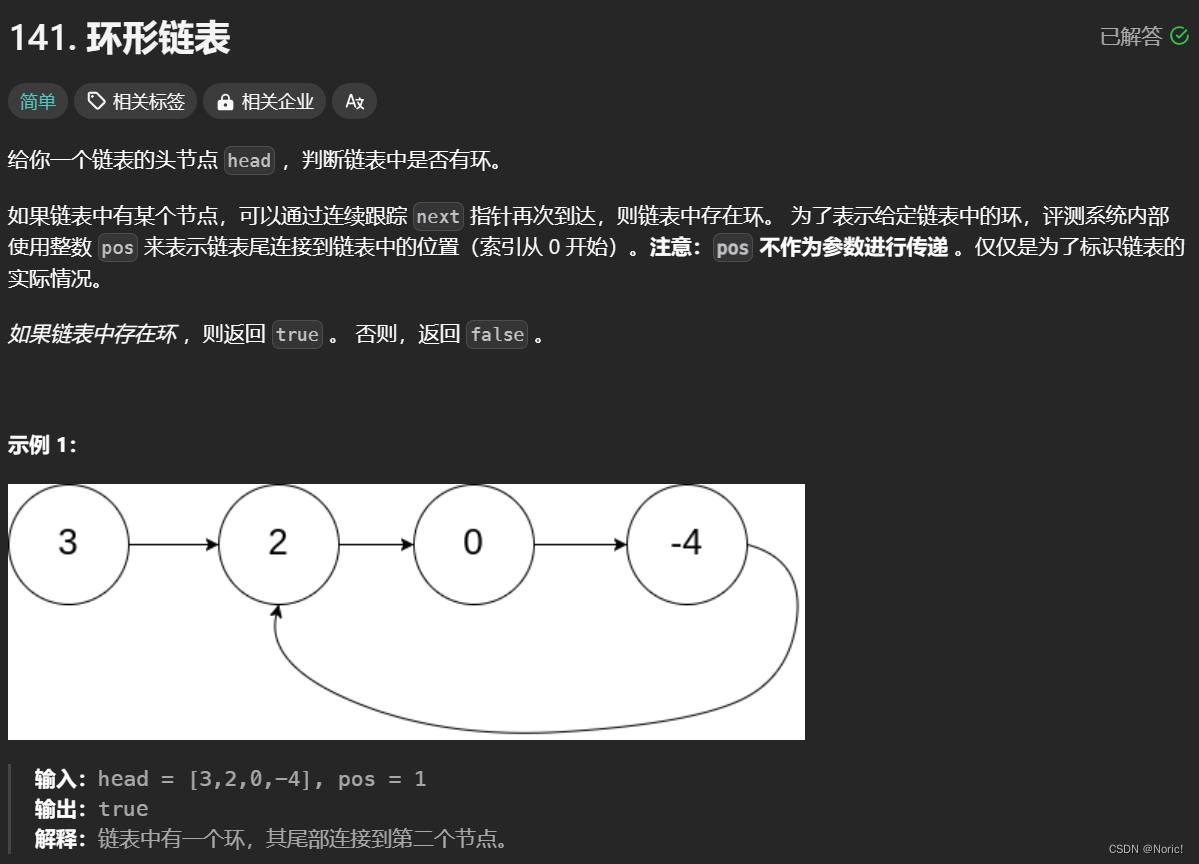
解题思路：
\qquad 最容易想到的方法，就是遍历链表同时用哈希表unordered_map把节点存下来：
\qquad\qquad 遇到重复节点则认为存在环，返回true；
\qquad\qquad 遍历到nullptr，则链表中不存在环，返回false；
\qquad 这种方法简单直接，时间复杂度O(N)，空间复杂度O(N)。但能不能更进一步优化空间复杂度到O(1)？

优化思路：
\qquad 借用双指针的思路，用快慢指针进行优化。
\qquad 慢指针slow每次前进1步，快指针fast每次前进两步。如果链表不存在环，则fast会比slow先到达终点nullptr；否则，fast会在环中绕圈，直到某一时刻与slow相遇。存在环的条件下，如何证明两指针一定会享相遇呢？假设经过x次移动后相遇，则fast移动的距离是2x，slow移动的距离是x，且满足以下等式：
\qquad 2x - x = n * LEN, 即 x = n * LEN \qquad LEN - 为链表中环的长度
\qquad 由于x为所有自然数，所以一定能够到达。

class Solution {
public:
    bool hasCycle(ListNode *head) {

        if(head == nullptr || head->next == nullptr)
        {
            return false;
        }
        ListNode * fast = head->next;
        ListNode * slow = head;

        while(fast != slow)
        {
            if(fast == nullptr || fast->next == nullptr)
            {
                return false;
            }
            fast = fast->next->next;
            slow = slow->next;
        }
        return true;
    }
};