=学习参考链接==
博客
分配问题与匈牙利算法
带你入门多目标跟踪(三)匈牙利算法&KM算法
视频
运筹学 | 例题详解指派问题
前言
- 图论-匈牙利算法原理参见上述参考连接中的博客与BiliBili博主的学习视屏,讲的很好很透彻。强烈建议看完(明白行列变换、找独立零、打勾、划线原理后)再来撸代码。
- 此处以成本矩阵求解n*n的最优分配问题。
问题描述
在实际中经常会遇到这样的问题,有n项不同的任务,需要 n个人分别完成其中的一项,但由于任务的性质和各人的专长不同,因此各人去完成不同的任务的效率(或花费的时间或费用)也就不同。于是产生了一个问题,应指派哪个人去完成哪项任务,使完成 项任务的总效率最高(或所需时间最少),这类问题称为分配问题或指派问题。
matlab代码实现
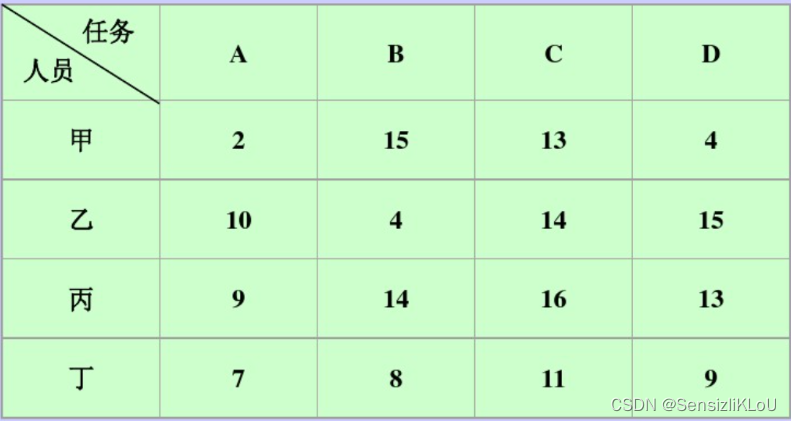
cost矩阵(n*n)
🔺 mainHA1.m
% 定义成本矩阵
costMatrix=[2,15,13,4;10,4,14,15;9,14,16,13;7,8,11,9];
% 调用匈牙利算法计算分配的结果,已经总成本
[f,D,G]=assign(costMatrix);
匈牙利算法实现主体
🔺 assign.m
function[f,D,G]=assign(B)
% 匈牙利算法实现
% u 和 v 是包含矩阵 B 沿每一行和每一列的最小值的向量
% 从矩阵 B 的相应行和列中减去这些最小值
n=length(B(:,1));
u=min(B,[],2);
f=sum(u);%用于记录最优值
B=B-repmat(u,1,n);
v=min(B,[],1);
f=f+sum(v);%用于记录最优值
B=B-repmat(v,n,1);
C=zeros(n);
while 1
% 在当前矩阵 B 中找到零元素,并在辅助矩阵 C 中进行标记
C(find(B==0))=1;
% 计算辅助矩阵 C 中每行和每列的和,存储在 u 和 v 中。
E=C;
u=sum(C,2);
v=sum(C);
% 调用 assignz 函数,该函数通过修改 C、D、G、E、u 和 v 来找到零元素的匹配。
D=zeros(1,n);
G=zeros(1,n);
[C,D,G,E,u,v]=assignz(C,D,G,E,u,v);
num=-1;
while num<0
add=find(D==0);
if isempty(add)
return;
end
% 调用 assignln 函数,该函数寻找未被覆盖的行,并从中找到一条增广路径
[D,G,E,SP,TP]=assignln(D,G,E,add);
num=numel(SP)-numel(TP);
end
% 更新矩阵 B,通过减去路径中的最小值,并在路径上加上最小值
add=setdiff(1:n,TP);
m=min(min(B(SP,add)));
B(SP,add)=B(SP,add)-m;
add=setdiff(1:n,SP);
B(add,TP)=B(add,TP)+m;
% 更新总成本 f,通过累加路径上的最小值与路径长度的乘积
f=f+m*num;
end
标记独立零元素
assignz.m
function[C,D,G,E,u,v]=assignz(C,D,G,E,u,v)%标记独立零
while any(u)
% % 找到第一个u为1的行
row=find(u==1,1);
while row
% 找到该行中第一个被标记为1的列
col=find(C(row,:)==1);
% 更新匹配关系
D(row)=col;
G(col)=row;
E(row,col)=0;
% 更新u和v
u=u-C(:,col);
% 清零相应的行和列
v(col)=0;
C(:,col)=0;
row=find(u==1,1);
end
% 找到第一个v为1的列
col=find(v==1,1);
while col
% 找到该列中第一个被标记为1的行
row=find(C(:,col)==1,1);
% 更新匹配关系
D(row)=col;
G(col)=row;
E(row,col)=0;
v=v-C(row,:);
u(row)=0;
C(row,:)=0;
col=find(v==1,1);
end
% 如果u仍有非零元素,则找到u和v的非零元素的位置
if any(u)
row=find(u,1);
col=find(C(row,:),1);
D(row)=col;
G(col)=row;
E(row,col)=0;
u=u-C(:,col);
u(row)=0;
v=v-C(row,:);
v(col)=0;
C(:,col)=0;
C(row,:)=0;
else return;
end
end
划线(以最少的线覆盖所有的零)—增广路径
assignln.m
function[D,G,E,SP,TP]=assignln(D,G,E,un)%作最少的直线覆盖所有零
S=un;
SP=[];
TP=[];
F=zeros(numel(D));
while ~isempty(S)
[null,T]=find(E(S,:));
T=setdiff(T,TP);
if isempty(T)
SP=union(SP,S);
return;
end
F(S,T)=E(S,T);
SP=union(SP,S);
TP=union(TP,T);
Stemp=G(T);
P=find(Stemp==0);
if ~isempty(P)
Tun=T(P);
[r,c]=find(E(S,Tun),1);
row=S(r);
col1=Tun(c);
while 1
E(row,col1)=0;
col2=D(row);
D(row)=col1;
G(col1)=row;
if ismember(row,un)
break;
end
E(row,col2)=1;
row=find(F(:,col2),1);
col1=col2;
end
SP=[];
return;
end
S=Stemp;
end
SP=[];
运行main函数可得最短时间为28
% 输出如下
f = 28
D = 4 2 1 3
G = 3 2 4 1
f为总的时间成本,D为员工,G为任务,即员工4对应3号任务。这是最优的分配结果。
匈牙利算法实例应用
问题描述:n个点从起始位置到目标位置,如何让成本最少???
分析:以欧式距离构建成本矩阵cost
计算每个点到目标点的距离,构建权重代价
getDistance.m
function [Distance] = getDistance(Agent,Goal)
n=length(Agent(:,1));
m=length(Goal(:,1));
for i=1:n
for j=1:m
Distance(i,j)=(Agent(i,1)-Goal(j,1))^2+(Agent(i,2)-Goal(j,2))^2;
Distance(i,j)=sqrt(Distance(i,j));
end
end
end
修改mainHA1.m函数
mainHA2.m
Agent=[-5,0;0,-1;0,-2;0,-3;-1,0;-1,-1;-1,-2;-1,-3;-2,0;-2,-1;-2,-2;-2,-3;-2,-4;-2,-5];
Goal=[5,5;6,6;7,7;8,8;4,6;3,7;2,8;2,9;8,9;3,10;7,10;4,10;6,10;5,9];
matrix=getDistance(Agent,Goal);
% 执行匈牙利算法,返回分配结果
[f,D,G]=assign(matrix);
% 使用 plot 函数绘制了连接线,同时在图中用蓝色和红色分别标记位置
num=length(D);
for i=1:num
plot([Agent(i,1),Goal(D(i),1)],[Agent(i,2),Goal(D(i),2)])
hold on
plot(Agent(i,1),Agent(i,2),'.','Color','b','MarkerSize',50);
hold on
plot(Goal(D(i),1),Goal(D(i),2),'.','Color','r','MarkerSize',50);
hold on
end
set(gca,'XminorGrid','on');
set(gca,'YminorGrid','on');axis equal
hold off
运行main函数可得最短距离为168.3064
- 下面是各个点的分配结果
f =
168.3064
D =
8 11 2 4 12 14 5 1 7 10 6 13 9 3
G =
8 3 14 4 7 11 9 1 13 10 2 5 12 6
- 结果显示如图
连线表示各个点的分配结果

🐑 🐑 🐑 🐑 🐑 🐑 🐑 🐑 🐑 🐑 🐑 🐑 🐑 🐑 🐑 🐑 🐑 🐑 🐑 🐑 🐑 🐑 🐑 🐑 🐑 🐑 🐑 🐑 🐑 🐑 🐑 🐑 🐑 🐑
博文中代码整理后的下载链接