作者在前段时间的一篇文章中介绍过了蜣螂优化算法(dung beetle optimizer，DBO)的原理及实现，该算法是由东华大学沈波教授团队在2022年提出[1]，其灵感来自蜣螂的滚球、跳舞、觅食、偷窃和繁殖行为这5种习性，其不同的子种群执行了不同的搜索方法，能够实现对空间的高效探索和开发，较之PSO、WOA和HHO等具有求解精度更高、收敛速度更快、稳定性更强等优点。

虽然蜣螂优化算法具有以上特点，但其同样有其他SI算法存在的问题，如全局探索和局部开发能力不平衡、面对复杂问题的易陷入局部最优等，其收敛速度和精度仍有改进的可能，因此本文将尝试对蜣螂优化算法进行改进以提升其性能。

00 文章目录

1 蜣螂优化算法原理

2 多策略融合的改进蜣螂优化算法

3 代码目录

4 实验结果

5 源码获取

01 蜣螂优化算法原理

关于蜣螂算法原理作者在前面文章中已经作了介绍

由蜣螂优化算法的原理可以得出其基本特点：其主要由四种行为（滚球、繁殖/育雏、觅食、偷窃）进行位置更新，滚球行为能够使算法在各阶段都具有较好的全局搜索能力；而繁殖行为与觅食行为则会让蜣螂分别围绕自身和最佳个体的位置进行探索，并随着迭代的进行，其搜索的动态边界将逐渐减小，其搜索范围也将逐渐缩小；偷窃行为则是在最佳个体附近进行动态的局部搜索。

02 多策略融合的改进蜣螂优化算法

本文基于蜣螂优化算法的特点及其缺陷进行如下改进。

2.1 改进的Circle混沌映射初始化

DBO通过随机生成初始种群的方法，容易出现种群分布不均匀，会导致种群多样性减少，种群质量不高，影响算法的收敛速度。

而混沌映射具有随机性、非重复性和混沌遍历性等特点［2］，意味着它比依赖于概率的随机生成更能够使种群分布均匀。因此，可以利用混沌映射生成初始种群来增加潜在解的多样性。目前文献中常用的混沌映射有Logistic映射、Tent映射和Circle混沌映射等，而Circle映射较为稳定且其混沌值覆盖率高[3]，但同时考虑到Circle映射在[0.2,0.6]之间取值较为密集，其分布并不均匀，因此对Circle映射公式进行改进[4]，使其更加均匀。

分别用Logistic映射、Tent映射、改进的Circle映射作出其分布图：

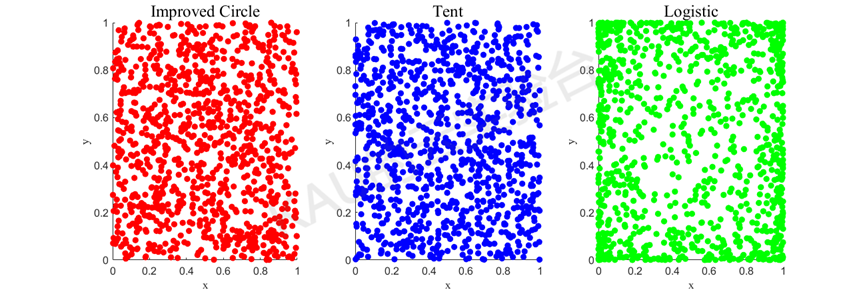
由结果可以看到，Logistic映射中间取值概率比较均匀,但在两端概率特别高，因此当全局最优点不在设计变量空间的两端时,对寻找最优点是不利的；其次Tent映射虽有较好的遍历性，但其迭代序列中存在小周期, 还存在不稳定周期点，因此若序列落入其中将导致序列趋于稳定，算法失效；最后，改进的Circle映射相对更加稳定且分布均匀性较好。

因此本文选用改进的Circle映射初始化DBO的种群, 以提高和改善初始种群在搜索空间上的分布质量，加强其全局搜索能力。

2.2 非线性边界收敛因子

由DBO的更新策略可知，其繁殖行为和觅食行为被限制在一定区域内，即产卵区域和觅食区域：

虽然其产卵和觅食区域随迭代次数动态调整，但这样的线性减少的策略难以表征其在繁殖与觅食时的复杂情况，我们希望算法在前期对全局可行区域进行更为广泛的搜索，而在后期更加注重在最优解附近的局部开发，加快其收敛速度。因此重新设置边界收敛因子R表达式如下：

改变前后的收敛因子迭代变化情况如下：

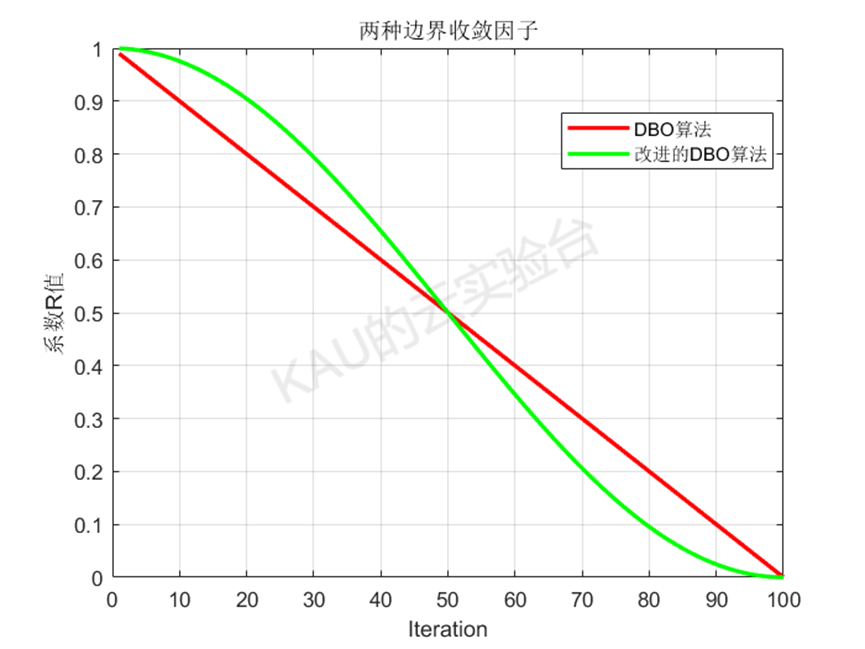
从图中可以看出，改进后的边界收敛因子相对于DBO中的收敛因子在前期下降得更慢，可以使觅食和产卵区域更大，从而获得更佳的全局勘探能力，而在后期，改进后的边界收敛因子相对于DBO中的收敛因子在后期下降得更快，从而加快了算法的收敛速度。

2.3 变螺旋搜索行为

鲸鱼在搜寻猎物的时候，会根据目标位置（即最优位置）与自身位置之间的螺旋形状整每次位置更新的移动距离，这种策略能够极大程度上利用区域信息，提高搜索能力。

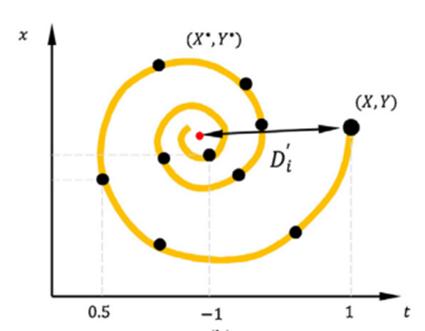
[图源: WOA-TLBO: Whale optimization algorithm with Teaching-learning-based optimization for global optimization and facial emotion recognition]

而在DBO中的滚球行为中，其并没有明确的有效目标指引，这样虽然有利于全局勘探，但可能导致算法过于随机，缺乏个体之间的信息交流，在后期不利于算法收敛，因此本文将螺旋更新机制引入蜣螂的滚球行为中。同时在螺旋搜寻的模型中，b控制个体前进时螺旋线的形状，其通常取值为1，但这种策略可能会导致更新时都按照固定螺旋接近猎物，可能会降低其全局寻优的能力，因此本文将该参数设计为动态变量，以一种变螺旋路径的方式增强算法对区域的探索能力，提高算法的全局搜索能力。

引入此变螺旋更新机制。

该改进策略将进一步协调DBO的全局的探索与局部开发的能力，并增强算法跳出局部最优的能力。

2.4 ‘劣汰’机制

受自然界中适者生存的法则启发，本文引入‘劣汰’机制提高种群解的质量，通过在每次迭代期间按照一定规则淘汰更新一些较差个体增强种群多样性，改善种群整体适应度以提高算法在复杂问题中的性能，并加快收敛速度。

具体来说，在每次迭代中，将具有较差适应度的个体将定义为Xw，然后基于最佳个体与1个随机选择的个体生成新个体Xnew。随机个体Xrand的引入为新个体的生成提供了一定随机性。

2.5 参数自适应调整

由蜣螂偷窃行为的更新方式可知，该行为倾向于在最优位置(最佳食物来源)进行局部搜索：

但此种策略可能导致小偷蜣螂在迭代过程中的快速同化，即迅速聚集到最优位置附件的区域，可能导致该种群陷入局部最优，使得搜索停滞。因此，我们希望在迭代前期尽可能扩大搜索范围，增加种群多样性，而在迭代后期能够在最优解附件进行更为准确的寻优。

由Levy飞行和布朗运动的运动特性可知，无论是Levy飞行的小步长与偶尔的远跳交替机制，还是布朗运动在控制区域能够实现宽轨迹运动的特性，这两种方法都不能实现在单个区域内的全局和局部搜索。然而，研究证明[5]，若将两种搜索策略联合起来，能够同时实现全局勘探和局部开发，弥补双方的不足，比单一的搜索策略更有效。因此本文将这两种策略融入偷窃行为中，既平衡了寻优的需求，其随机运动也能提高算法跳出局部最优的能力。

两种运动的模拟图如下：

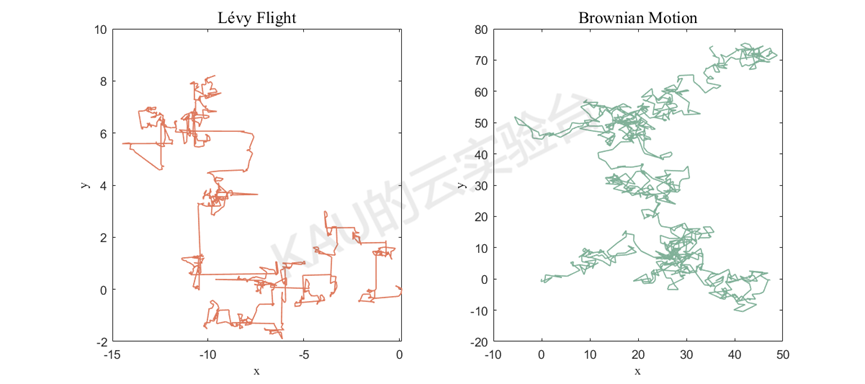
2.5.1 布朗运动

在迭代前期，小偷蜣螂容易快速向最优个体靠近，导致种群多样性不足，易使算法陷入局部最优。因此本文将标准布朗运动引入偷窃行为前期的位置更新公式，增加蜣螂个体的多样性，从而提高算法的全局探索能力。

2.5.2 莱维飞行

在迭代后期，小偷蜣螂的位置将聚集于当前最优个体附近，过于集中的分布可能使得算法进化停滞，陷入局部最优。而莱维飞行是以偶尔长程跳跃为特点的一类具有马尔科夫性质的非高斯随机游走过程，既有小范围游走也有大距离跳跃，小范围游走能够帮助算法进行局部邻域搜索，提高寻优精度，长距离跳跃能对种群位置进行扰动，帮助算法进行探索，跳出局部最优。因此将莱维飞行引入小偷蜣螂迭代后期的位置更新​。

2.6 算法流程​

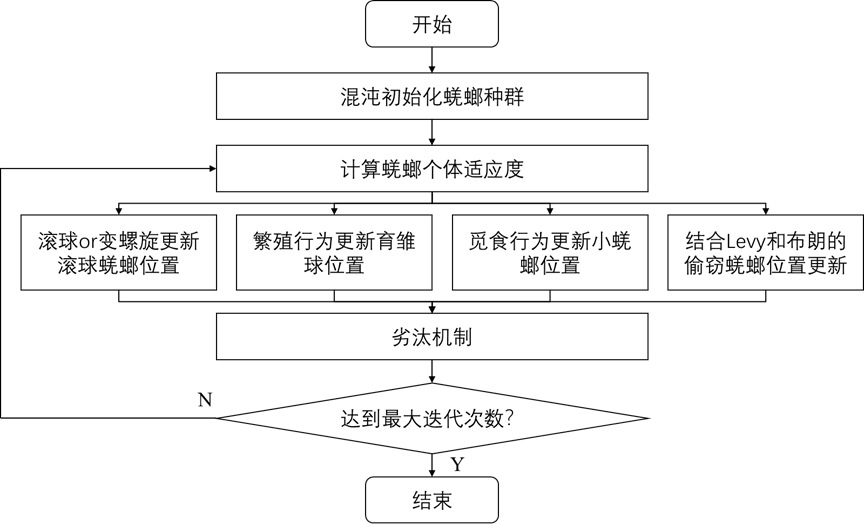
03 代码目录

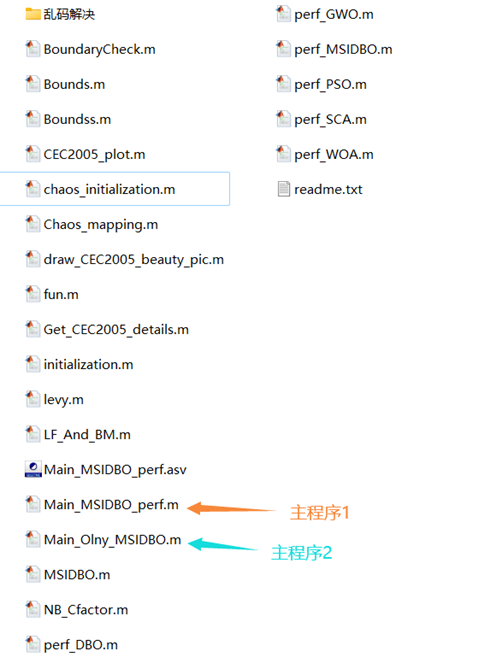
其中，Main_MSIDBO_perf.m和Main_Only_MSIDBO.m为主程序，关于这两个主程序的使用在readme.txt中作者做了解释：

代码注释详细，一键运行Main_MSIDBO_perf.m即可得到所有运行结果，运行结果包括混沌序列比较图、收敛因子比较图、Levy和布朗比较图以及算法在各测试函数上的迭代图，最后将生成excel表，包含算法在各函数迭代n次的平均值，均值、运行时间、最优解。

同时，文件也有乱码解决，给出了主要代码的txt文件。

部分程序如下：

Main_Only_MSIDBO.m

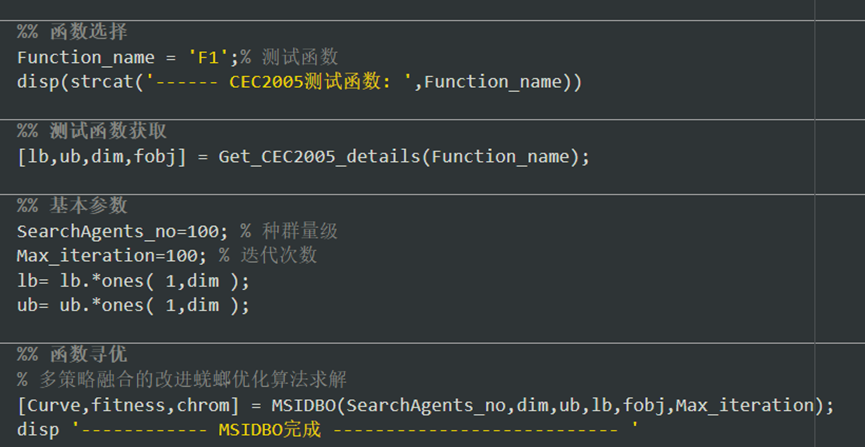
改进的DBO部分

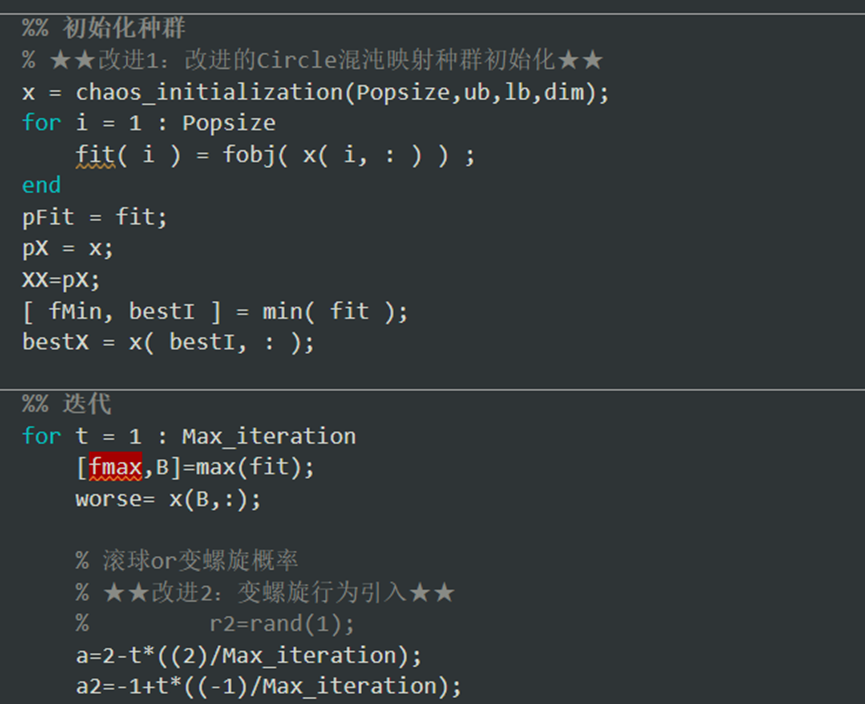
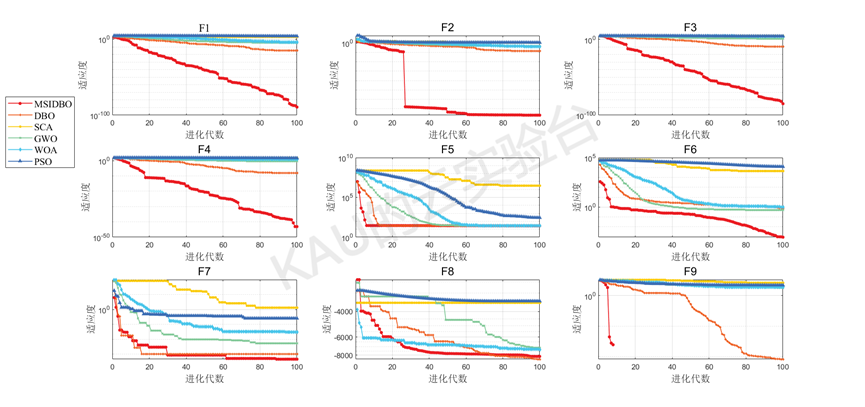
04 实验结果

在本节中，经过23个经典测试函数验证MSIDBO的搜索性能，将改进的蜣螂优化算法与另5种被广泛研究的优化算法(PSO、WOA、SCA、GWO、DBO)进行比较。

为保证实验公平性，所有算法的迭代次数与种群数都设置为100。

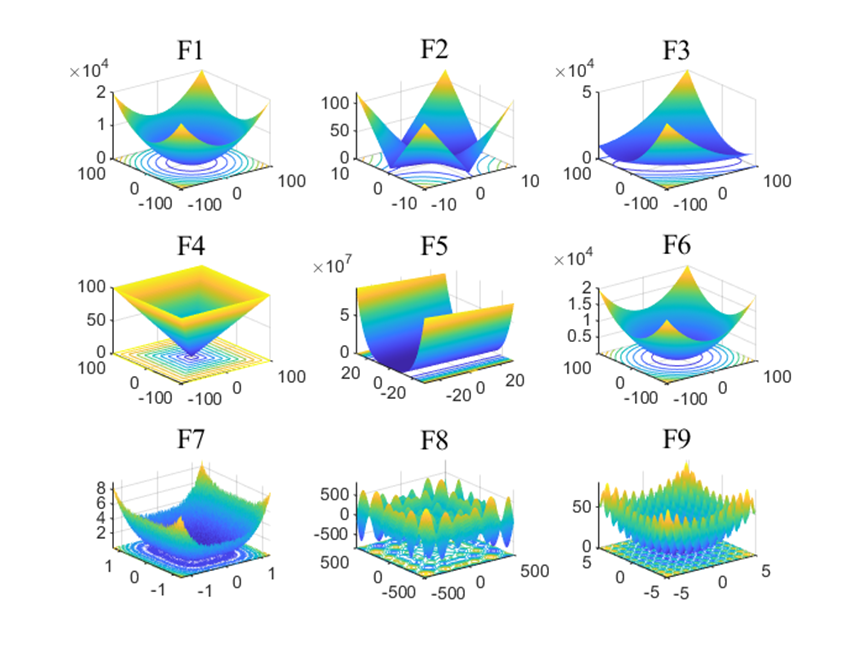
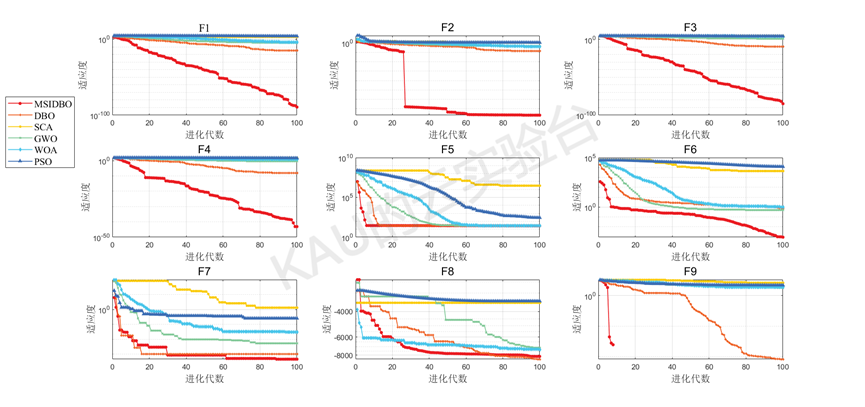
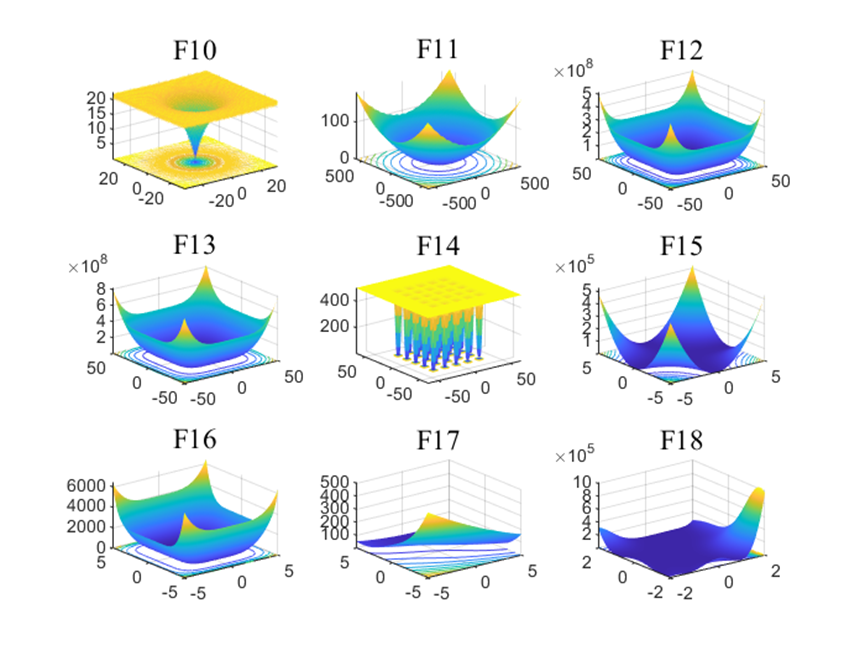
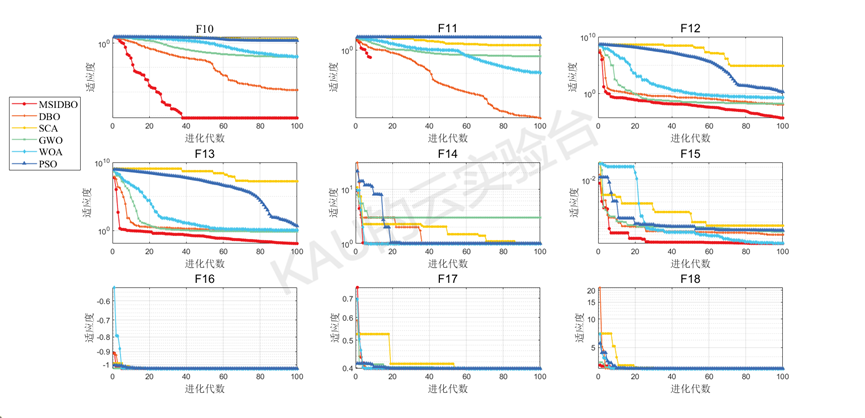
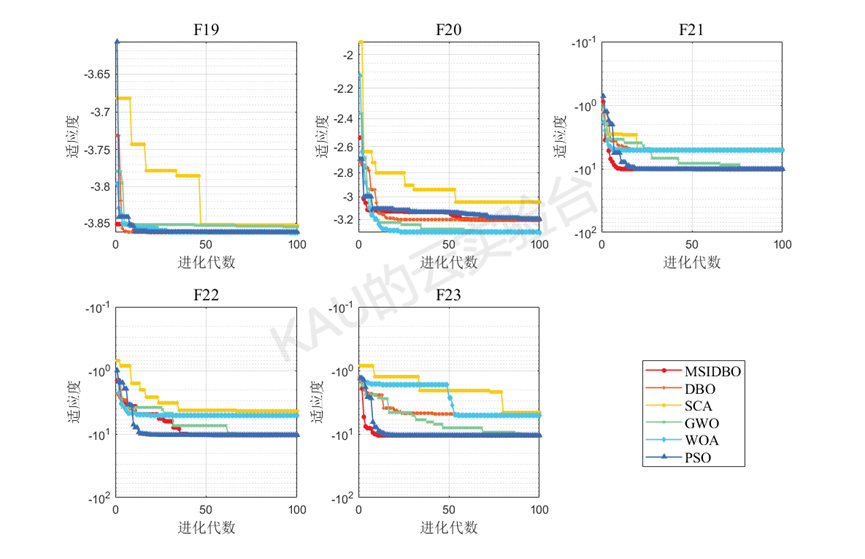
仅运行MSIDBO的主程序得到的结果：

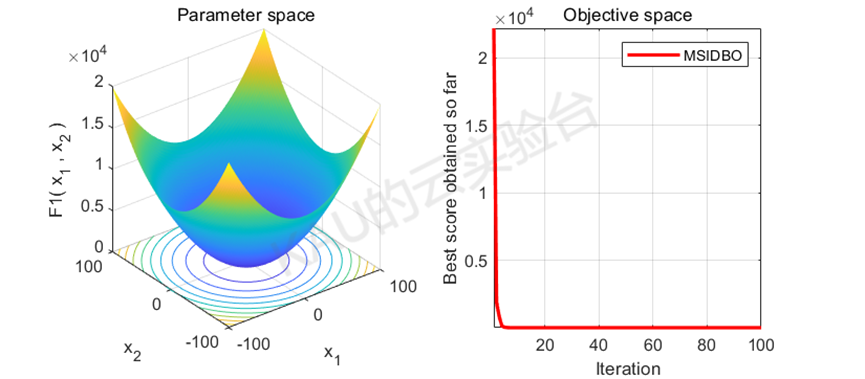
05 源码获取

在GZH（KAU的云实验台）后台回复：MSIDBO

除代码外，文件还包含完整的原理说明及其公式

参考文献

[1] XUE J K, SHEN B. Dung beetle optimizer: A new metaheuristic algorithm for global optimization [ J ]. The Journal of Supercomputing, 2023, 79(7): 7305-7336.

[2] Shi X,Li M. Whale Optimization Algorithm Improved Effectiveness Analysis Based on Compound Chaos Optimization Strategy and Dynamic Optimization Parameters [c]//2019 International Conference on Virtual Reality and Intelligent Systems( ICVRIS) . 2019:123-126.

[3]ZHANGD M, XU H, WANG Y R, et al. Whale optimization algorithm for embedded Circle mapping and onedimensional oppositional learning based small hole imaging[J]. Control and Decision, 2021, 36(5): 1173-1180（in Chinese）.

[4] 宋立钦,陈文杰,陈伟海等.基于混合策略的麻雀搜索算法改进及应用[J].北京航空航天大学学报,2023,49(8):2187-2199.

[5] Bartumeus F, Catalan J, Fulco U L, et al. Optimizing theEncounter Rate in Biological Interactions: Levy Versus Brownian Strategies[J]. Physical Review Letters，2002,88(9): 097901.

[6] MANTEGNA RN.Fast，accurate algorithm for numericalsimulation of Levy stable stochastic processes [J]. PhysicalReview. E，Statistical Physics，Plasmas，Fluids，and RelatedInterdisciplinary Topics，1994,49(5): 4677-4683.

另：如果有伙伴有待解决的优化问题（各种领域都可），可以发我，我会选择性的更新利用优化算法解决这些问题的文章。

如果这篇文章对你有帮助或启发，可以点击右下角的赞/在看 (ง•̀_•́)ง(不点也行)