目录
今天知识点
求交点转化求逆序对,每次操作都维护一个y点的前缀和
树的变动转化成一维数组的变动,利用时间戳将节点转化成区间
离散化数组来求逆序对数
先将y排序,然后每加入一个就点更新求一次前缀和
POJ3067:日本
思路:
POJ3321苹果树:
思路:
快排变形:
思路:
POJ2352:星星
思路:
POJ3067:日本
东海岸有n个城市,西海岸有m个城市,每个海岸的城市从北到南编号为1,2……,每条高速公路都是直线,连接东西海岸的城市。求公路的交叉点数
输入:
1
3 4 4
1 4
2 3
3 2
3 1
思路:
根据样例画出草图:按照1 4,2 3,3 1,3 2的顺序去画,很容易发现只要出现逆序对就会产生交点。
定义逆序对:(x1,y1)和(x2,y2)为逆序对,则等价于x1<x2且y1<y2。
所以在画2 3时候产生了一个逆序对,画3 1时候产生了2个逆序对,画 3 2时候也产生了两个逆序对。故最终5个交点。

所以这道题就是求逆序对数。
因为比如两边都同时大于或小于。我们先对x排序(若x相等,则y升序),然后按x的顺序检查每条边,统计y的前缀和,因为当前已经连了i条边,那么y的前缀和数就一定是非逆序对数。所以i减去y的前缀和就是逆序对数。
这道题就变成了每次增加一个元素就前一次对应的前缀和问题。因此我们只需要对每个点y维护一个关于y的前缀。每次操作后都要给对应点y加个1
#include <bits/stdc++.h>
using namespace std;
#define maxn 1010
#define maxk 1000010
#define lowbit(x) (x)&(-x)
typedef long long ll;
int c[maxn],kas,n,m,k;
struct edge{int x,y;}e[maxk];
bool cmp(edge a,edge b){
return a.x<b.x||(a.x==b.x&&a.y<b.y);
}
void add(int i){//加1操作,参数省略
while(i<=m){
++c[i];
i+=lowbit(i);
}
}
int sum(int i){
int s=0;
while(i>0){
s+=c[i];
i-=lowbit(i);
}
return s;
}
int main(){
int t;cin>>t;
while(t--){
memset(c,0,sizeof(c));//每个样例都要清空一次树状数组。
scanf("%d%d%d",&n,&m,&k);
for(int i=0;i<k;i++)
scanf("%d%d",&e[i].x,&e[i].y);
sort(e,e+k,cmp);//默认升序
ll ans=0;
for(int i=0;i<k;i++){
ans+=i-sum(e[i].y);//累加逆序对
add(e[i].y);//加入进去
}
printf("Test case %d: %lld\n",++kas,ans);
}
}
POJ3321苹果树:
一个苹果树上有n个叉,通过分支连接,我们将叉从1到n进行编号,每个叉上最多只会有一个苹果,且苹果树上一开始长满了苹果。
卡卡可能会从树上摘一个苹果,树上的空叉可能又会长出新的苹果。
输入:
第一行n表示叉数。
以下n-1行是两个整数u和v表示之间有叉相连
以下m行表示m条消息
C x表示叉x上的苹果变化了:有过原来有则现在没有,原来没有则现在有了
Q x表示叉x上方子树中的苹果数量,包括x叉上的苹果(如果存在的话)
3
1 2
1 3
3
Q 1
C 2
Q 1
思路:
我们先把树倒过来,既然要统计每个节点的变动,每变动一次就统计一次不现实。
那就把树所有节点按照dfs顺序映射成一维数组a,再利用时间戳就把求节点孩子问题变成了求时间戳的区间和问题
既要统计a的区间和又要考虑到节点的变动,那就创建树状数组c来维护a。节点的变动恰好对应了点更新。
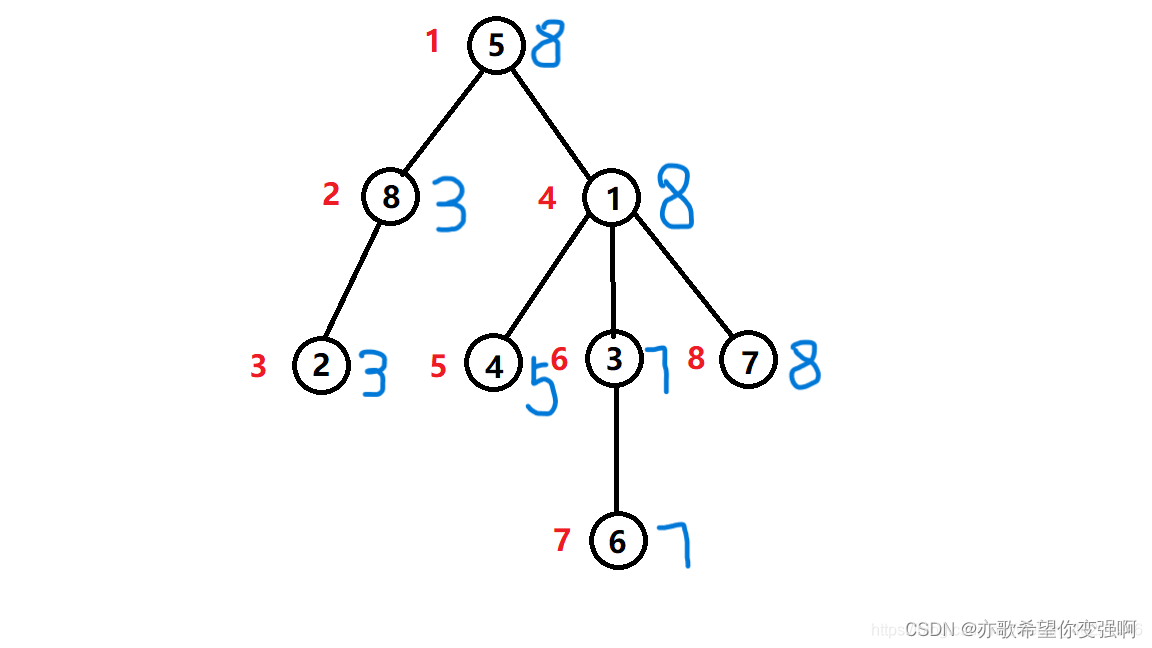
红色代表L,蓝色代表R, 可见每个点的时间戳,不难看出每个节点的R-L就是这个节点的孩子数量
#include <bits/stdc++.h>
#define lowbit(x) (x)&(-x)//求区间长度
using namespace std;
const int maxn=1e5+10;
int n,q;
int c[maxn],a[maxn];
int L[maxn],R[maxn];
int head[maxn];
int cnt,dfn;
struct edge{int u,v,next;}e[2*maxn];
void adde(int u,int v){e[++cnt]={u,v,head[u]};head[u]=cnt;}
int sum(int i){//求前缀和,
int ans=0;
for(;i>0;i-=lowbit(i)) ans+=c[i];
return ans;
}
void add(int i,int val){//在第i点上加val,修改找后继
for(;i<=n;i+=lowbit(i)) c[i]+=val;
}
void init(){
memset(c,0,sizeof(c));
memset(L,0,sizeof(L));
memset(R,0,sizeof(R));
memset(head,0,sizeof(head));
cnt=0;dfn=0;//因为深度优先的序列是从1开始的
for(int i=1;i<=n;i++)a[i]=1,add(i,1);//a[i]是1表示该分支i上有苹果
}
void dfs(int u,int fa){//之所以写fa,是防止走父子边,这样子的话vis就不再需要了
L[u]=++dfn;//相当于是时间戳,根节点是1
for(int i=head[u];i;i=e[i].next){
int v=e[i].v;
if(v==fa)continue;
dfs(v,u);
}
R[u]=dfn;//记录时间戳
}
int main(){
cin>>n;
int u,v;
init();
for(int i=1;i<n;i++){
scanf("%d%d",&u,&v);
adde(u,v);
}
dfs(1,1);
cin>>q;
char op[10];//之所以定义字符串,就是因为字符型于回车不兼容,所以换成字符串输入不怕回车
for(int i=1;i<=q;i++){
getchar();
scanf("%s %d",op,&v);//不用考虑回车问题
if(op[0]=='C'){
if(a[L[v]]) add(L[v],-1);
else add(L[v],1);
a[L[v]]^=1;//0变1,1变0
}
else{
int s1=sum(R[v]);
int s2=sum(L[v]-1);
printf("%d\n",s1-s2);
}
}
}
快排变形:
有n个数,每次通过临项交换来数组中的元素变成升序排列,问需要经过多少次交换?
输入5 4 1 2 999999999 输出5
思路:
就是求逆序对数。输入4时有一个逆序对,再输入1有两个,再输入2有两个,再输入99999999有零个。共五个。
因为我们要在输入数时求小于此数前缀和,可以将数值当成下标存入树状数组来求前缀和,但是数值过大就必须离散化处理,把数值变成排名。
比如:5 4 1 2 999999999 变成4 3 1 2 5即可。
方法:先创建一个排序后的暂存数组,然后按每个数的名次进行赋值对原数组修改即可。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=10000;
ll ans,c[maxn];//c[]为树状数组
int n,a[maxn],b[maxn];
int lowbit(int i){ return (-i)&i;}
void add(int i,int z){ for(;i<=n;i+=lowbit(i)) c[i]+=z;}
ll sum(int i){
ll s=0;
for(;i>0;i-=lowbit(i)) s+=c[i];
return s;
}
int main(){
cin>>n;
//进行离散化
for(int i=1;i<=n;i++)cin>>b[i],a[i]=b[i];
sort(b+1,b+1+n);
for(int i=1;i<=n;i++)
a[i]=lower_bound(b+1,b+1+n,a[i])-b;
//开始求前缀和
for(int i=1;i<=n;i++){
ans+=i-sum(a[i])-1;
add(a[i],1);
}
cout<<ans;
return 0;
}
/*//离散化实例
#include <bits/stdc++.h>
using namespace std;
int a[100],b[100];
int main(){
int n;cin>>n;
for(int i=1;i<=n;i++)cin>>b[i],a[i]=b[i];//实现离散化,把数值变成相对排名,然后数值当成下标存储个数统计前缀和
sort(b+1,b+1+n);
for(int i=1;i<=n;i++){
cout<<a[i]<<' ';
a[i]=lower_bound(b+1,b+1+n,a[i])-b;
cout<<a[i]<<' '<<'\n';
}
}
5
5 4 1 2 999*/
POJ2352:星星
在平面上有n个星星,每颗星星都有自己的坐标。规定星星的等级数为纵横坐标均不超过自己的星星数量(不包括自己),请输出每个级别的星星数量
输入保证y是递增的,且如果y相等,那么x是递增的。
5
1 1
5 1
7 1
3 3
5 5
思路:
看似是二维前缀和,实际上y是排好顺序的,那也就是说只需要按y的顺序计算每个x的前缀和即可。相当于加入一个x就统计一下x的前缀和。
#include<bits/stdc++.h>
using namespace std;
#define maxn 32005
#define lowbit(x) (x)&(-x)
int ans[maxn],c[maxn];
int n;
void add(int i,int val){
while(i<=maxn){
c[i]+=val;
i+=lowbit(i);
}
}
int sum(int i){//统计前缀和
int s=0;
while(i>0){
s+=c[i];
i-=lowbit(i);
}
return s;
}
int main(){
cin>>n;
int x,y;
for(int i=0;i<n;i++){
scanf("%d%d",&x,&y);
x++;//注意给的坐标x是从0开始的,树状数组的下标必须从0开始,所以都加1
ans[sum(x)]++;
add(x,1);//x的数量加1
}
for(int i=0;i<n;i++){//一共最多n-1个等级
printf("%d\n",ans[i]);
}
}







![[GFCTF 2021]文件查看器](https://img-blog.csdnimg.cn/direct/530b8a2f614f4b69a8eb2acfaf10b07c.png)