题目描述：

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

创建一个根节点，其值为 nums 中的最大值。
递归地在最大值 左边 的 子数组前缀上 构建左子树。
递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。

示例 1：

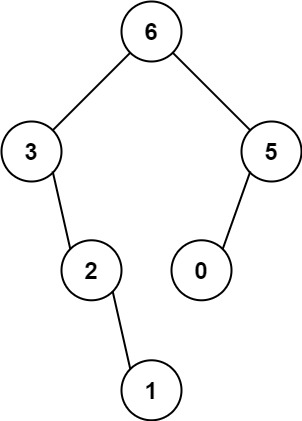
输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：

• [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
  • [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
    • 空数组，无子节点。
    • [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
      • 空数组，无子节点。
      • 只有一个元素，所以子节点是一个值为 1 的节点。
  • [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
    • 只有一个元素，所以子节点是一个值为 0 的节点。
    • 空数组，无子节点。

示例 2：

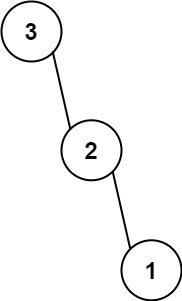
输入：nums = [3,2,1]
输出：[3,null,2,null,1]

提示：

1 <= nums.length <= 1000
0 <= nums[i] <= 1000
nums 中的所有整数 互不相同

解题思路一：递归，这个问题的难点在于如何找到每个子数组的最大值。此处用的是暴力查找最大值，然后递归构建左右子树。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:
        def construct(left: int, right: int) -> Optional[TreeNode]:
            if left>right: return None
            best = left
            for i in range(left + 1, right + 1):
                if nums[i] > nums[best]: best = i
            
            root = TreeNode(nums[best])
            root.left = construct(left, best - 1)
            root.right = construct(best + 1, right)
            return root

        return construct(0, len(nums)-1)

时间复杂度：O(n²)
空间复杂度：O(n)

解题思路二：单调栈，显然暴力解法非最优解。可以将任务转化为找出每一个元素左侧和右侧第一个比它大的元素所在的位置。这就是一个经典的单调栈问题了。如果左侧的元素较小，那么该元素就是左侧元素的右子节点；如果右侧的元素较小，那么该元素就是右侧元素的左子节点。细节看代码注释。

需要参考LeetCode-496. 下一个更大元素 I【栈 数组 哈希表 单调栈】和LeetCode-503. 下一个更大元素 II【栈 数组 单调栈】
关于更多的解释参考官方题解吧。最大二叉树

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:
        n = len(nums)
        stk = []
        left, right = [-1] * n, [-1] * n
        tree = [None] * n

        # 维护左右侧大值
        for i in range(n):
            tree[i] = TreeNode(nums[i])
            while stk and nums[i] > nums[stk[-1]]:
                # 右侧大值在出栈时维护
                right[stk[-1]] = i
                stk.pop()
            if stk: 
                # 左侧大值在出栈后维护
                left[i] = stk[-1]
            stk.append(i)
        
        root = None
        for i in range(n):
            # 如果左右都没有大值，说明是根节点
            if left[i] == right[i] == -1:
                root = tree[i]
            # 如果右侧没有大值，或者左侧大值小于右侧大值，那么该节点是左侧大值的右孩子
            elif right[i] == -1 or (left[i] != -1 and nums[left[i]] < nums[right[i]]):
                tree[left[i]].right = tree[i]
            # 如果右侧的元素较小，那么该元素就是右侧元素的左子节点。
            else:
                tree[right[i]].left = tree[i]
        return root

时间复杂度：O(n)
空间复杂度：O(n)

我们还可以把最后构造树的过程放进单调栈求解的步骤中，省去用来存储左右边界的数组。下面的代码理解起来较为困难，同一个节点的左右子树会被多次赋值，读者可以仔细品味其妙处所在。

class Solution:
    def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:
        n = len(nums)
        stk = list()
        tree = [None] * n

        for i in range(n):
            tree[i] = TreeNode(nums[i])
            while stk and nums[i] > nums[stk[-1]]:
                tree[i].left = tree[stk[-1]]
                stk.pop()
            if stk:
                tree[stk[-1]].right = tree[i]
            stk.append(i)
        
        return tree[stk[0]]

细细品味💪 💪 💪

解题思路三：0