文章目录
- Ch4.不定积分
- Ch5.定积分
- 1.定积分定义
- 定积分的几何意义
- 2.定积分性质
- 定积分的保号性
- 定积分中值定理
- 3.定积分的计算方法
- 1.凑微分
- 2.换元法
- 三角换元
- 3.分部积分
- 分部积分公式、原则
- 表格法
- 含变限积分f(x)的定积分:用分部积分凑f(x)的导数
- 4.区间再现
- 5.求定积分的公式
- 1.牛顿-莱布尼茨公式
- 2.点火公式/华里士公式/Wallis公式:
- 4.变限积分
- 1.变限积分求导
- 2.变限积分的连续性与可导性
- 5. 广义积分/反常积分
- 1.无穷限的广义积分
- 广义积分的计算
- 2.无界函数的反常积分 / 瑕积分
- 3.反常积分的审敛法
- 1.极限审敛法
- 2.比较审敛法
- 6.Γ函数
- Ch6.定积分应用
- 定积分的几何应用
- 定积分的物理应用
- 0.速度与路程
- 1.变力做功
- 2.水压力
- 3.引力
- Ch7.微分方程
Ch4.不定积分
原函数 F ( x ) F(x) F(x)
原函数F(x)定义:若有F’(x)=f(x),则称f(x)的原函数为F(x)。
原函数存在定理
f(x)连续,则必有原函数F(x)
不定积分 ∫ f ( x ) d x \int f(x)dx ∫f(x)dx
∫ f ( x ) d x = F ( x ) + C \int f(x)dx=F(x)+C ∫f(x)dx=F(x)+C
所以说不定积分要加C,不带C的那叫求 原函数F(x)。题目要的是不定积分,∫f(x)dx=F(x)+C
不定积分公式
1. ∫ s e c x d x = ln ∣ s e c x + t a n x ∣ + C \int {\rm sec}x{\rm d}x=\ln|{\rm sec}x+{\rm tan}x|+C ∫secxdx=ln∣secx+tanx∣+C
2. ∫ 1 1 − x 2 d x = 1 2 ln ∣ 1 + x 1 − x ∣ + C \int\dfrac{1}{1-x²}dx=\dfrac{1}{2}\ln|\dfrac{1+x}{1-x}|+C ∫1−x21dx=21ln∣1−x1+x∣+C
推导:
1.凑微分凑到巅峰造极
∫
sec
x
d
x
=
∫
s
e
c
x
(
s
e
c
x
+
t
a
n
x
)
s
e
c
x
+
t
a
n
x
d
x
=
∫
s
e
c
x
t
a
n
x
+
s
e
c
2
x
s
e
c
x
+
t
a
n
x
d
x
=
(
s
e
c
x
)
′
=
s
e
c
x
t
a
n
x
(
t
a
n
x
)
′
=
s
e
c
2
x
ln
∣
s
e
c
x
+
t
a
n
x
∣
+
C
\int \sec xdx=\int \dfrac{secx(secx+tanx)}{secx+tanx}dx=\int \dfrac{secxtanx+sec^2x}{secx+tanx}dx\xlongequal[(secx)'=secxtanx]{(tanx)'=sec^2x}\ln|secx+tanx|+C
∫secxdx=∫secx+tanxsecx(secx+tanx)dx=∫secx+tanxsecxtanx+sec2xdx(tanx)′=sec2x(secx)′=secxtanxln∣secx+tanx∣+C
2.拆两项
∫
1
1
−
x
2
d
x
=
1
2
∫
1
1
+
x
+
1
1
−
x
d
x
=
1
2
[
ln
∣
1
+
x
∣
−
ln
∣
1
−
x
∣
+
C
]
=
1
2
ln
∣
1
+
x
1
−
x
∣
+
C
\int\dfrac{1}{1-x²}dx=\dfrac{1}{2}\int\dfrac{1}{1+x}+\dfrac{1}{1-x}dx=\dfrac{1}{2}[\ln|1+x|-\ln|1-x|+C]=\dfrac{1}{2}\ln|\dfrac{1+x}{1-x}|+C
∫1−x21dx=21∫1+x1+1−x1dx=21[ln∣1+x∣−ln∣1−x∣+C]=21ln∣1−x1+x∣+C
例题1:11年9.
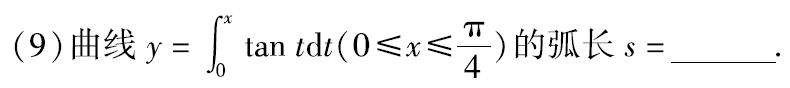
答案: ln ( 1 + 2 ) \ln(1+\sqrt{2}) ln(1+2)
例题2:22年18.

不定积分 ⇦⇨ 变上限积分: ∫ f ( x ) d x = ∫ 0 x f ( t ) d t \int f(x){\rm d}x=\int_0^xf(t){\rm d}t ∫f(x)dx=∫0xf(t)dt
例题1:18年18.(2) 微分方程、周期函数的定义

分析:为了凑周期函数的定义,将不定积分转化为变上限积分
答案:
Ch5.定积分
1.定积分定义
∫
a
b
f
(
x
)
d
x
=
lim
λ
→
0
∑
i
=
1
n
f
(
ξ
i
)
Δ
x
i
\int_a^bf(x)dx=\lim\limits_{λ→0}\sum\limits_{i=1}^nf(ξ_i)Δx_i
∫abf(x)dx=λ→0limi=1∑nf(ξi)Δxi
将[0,1]n等分,得:
∫
0
1
f
(
x
)
d
x
=
lim
n
→
∞
∑
i
=
1
n
f
(
i
n
)
⋅
1
n
\int_0^1f(x)dx=\lim\limits_{n→∞}\sum\limits_{i=1}^nf(\dfrac{i}{n})·\dfrac{1}{n}
∫01f(x)dx=n→∞limi=1∑nf(ni)⋅n1
例题1:10年4. 二重积分的定义
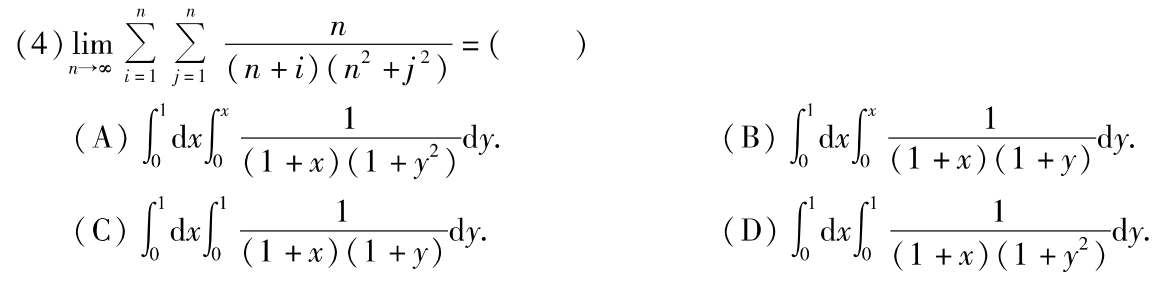
分析:
定积分、二重积分的定义都是0到1上的积分,排除AB
下面提出n×n²,与上面n约分得1/n²,应该选D
答案:D
定积分的几何意义
2.定积分性质
定积分的保号性
如果在区间
[
a
,
b
]
[a,b]
[a,b]上
f
(
x
)
≥
0
f(x)≥0
f(x)≥0,那么
∫
a
b
f
(
x
)
d
x
≥
0
(
a
<
b
)
\int_a^bf(x){\rm d}x≥0 \quad (a<b)
∫abf(x)dx≥0(a<b)
推论1:如果在区间
[
a
,
b
]
[a,b]
[a,b]上
f
(
x
)
≤
g
(
x
)
f(x)≤g(x)
f(x)≤g(x),那么
∫
a
b
f
(
x
)
d
x
≤
∫
a
b
g
(
x
)
d
x
\int_a^bf(x){\rm d}x≤\int_a^bg(x){\rm d}x
∫abf(x)dx≤∫abg(x)dx
即若积分区间相同,只需要比较在此区间内被积函数的大小,即为该区间上定积分的大小关系。
例题1:11年4. 定积分的保号性

分析:
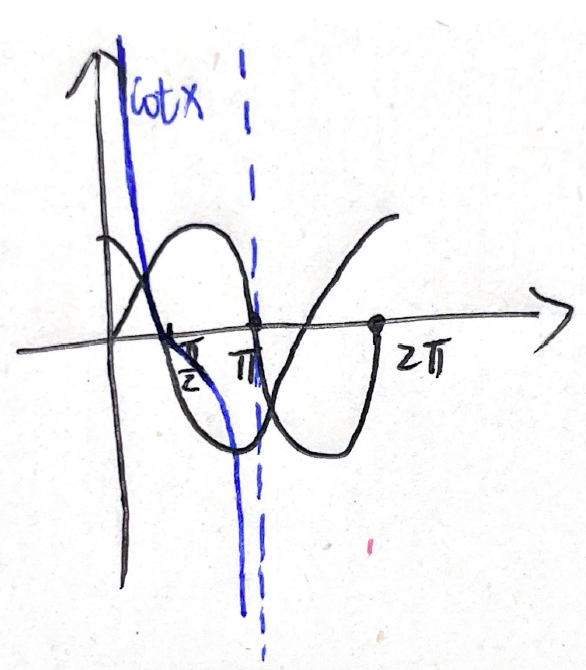
答案:B
例题2:18年4.
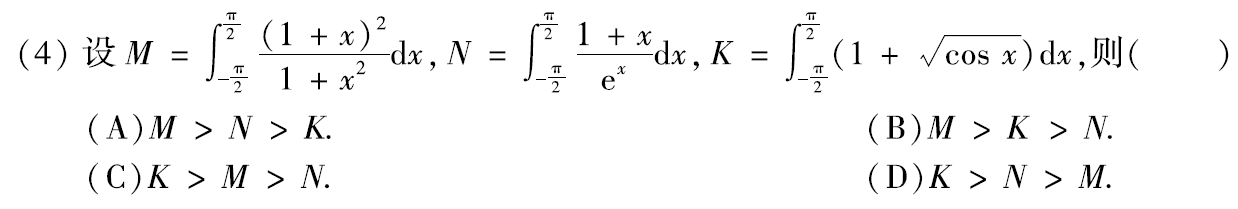
分析:积分区间都是 [ − π 2 , π 2 ] [-\frac{π}{2},\frac{π}{2}] [−2π,2π],只需比较该区间上被积函数的大小即可。
f M ( x ) = 1 , f N ( x ) = 1 + x e x , f K ( x ) = 1 + c o s x f_M(x)=1,f_N(x)=\dfrac{1+x}{e^x},f_K(x)=1+\sqrt{cosx} fM(x)=1,fN(x)=ex1+x,fK(x)=1+cosx
显然,当 − π 2 ≤ x ≤ π 2 -\frac{π}{2}≤x≤\frac{π}{2} −2π≤x≤2π时, 1 + c o s x > 1 > 1 + x e x 1+\sqrt{cosx}>1>\dfrac{1+x}{e^x} 1+cosx>1>ex1+x
答案:C
例题3:19年18.
定积分中值定理
定积分中值定理:如果函数f(x)在区间[a,b]上连续,那么在[a,b]上至少存在一个点ξ使下式成立:
∫
a
b
f
(
x
)
d
x
=
f
(
ξ
)
(
b
−
a
)
(
a
≤
ξ
≤
b
)
f
(
ξ
)
=
∫
a
b
f
(
x
)
d
x
b
−
a
(
a
≤
ξ
≤
b
)
\int_a^bf(x)dx=f(ξ)(b-a) \qquad (a≤ξ≤b)\\[3mm] f(ξ)=\dfrac{\int_a^bf(x)dx}{b-a} \qquad \qquad (a≤ξ≤b)
∫abf(x)dx=f(ξ)(b−a)(a≤ξ≤b)f(ξ)=b−a∫abf(x)dx(a≤ξ≤b)
②式称为函数f(x)在区间[a,b]上的平均值

定积分中值定理与拉格朗日中值定理的关系:
设f(x)为F(x)的导函数,F(x)在[a,b]上连续,f(x)在[a,b]上连续,(a,b)内可导,则在区间(a,b)内至少有一点ξ (a<ξ<b),使等式
f
(
ξ
)
=
中值定理
定积分
∫
a
b
f
(
x
)
d
x
b
−
a
=
公式
牛莱
F
(
b
)
−
F
(
a
)
b
−
a
=
中值定理
拉格朗日
F
′
(
ξ
)
f(ξ)\xlongequal[中值定理]{定积分}\dfrac{\int_a^bf(x)dx}{b-a}\xlongequal[公式]{牛莱}\dfrac{F(b)-F(a)}{b-a}\xlongequal[中值定理]{拉格朗日}F'(ξ)
f(ξ)定积分中值定理b−a∫abf(x)dx牛莱公式b−aF(b)−F(a)拉格朗日中值定理F′(ξ)
3.定积分的计算方法
1.凑微分
例题1:09年11. 定积分的计算:凑微分
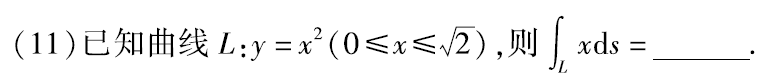
分析:
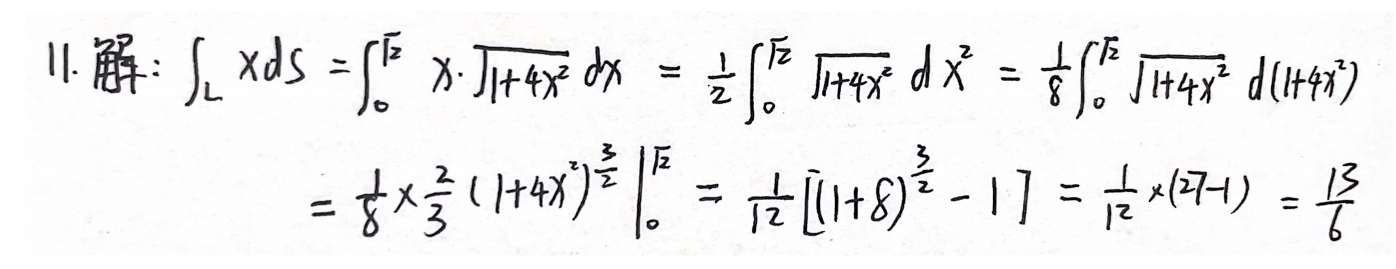
答案: 13 6 \dfrac{13}{6} 613
2.换元法
1.换元要换上下限
2.整体代换
例题1:23李林四(一)11. 换元法求定积分:整体代换
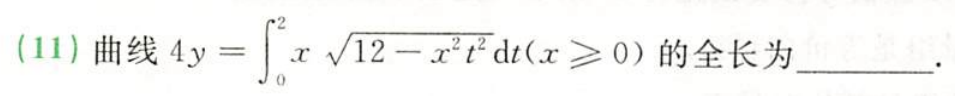
分析:
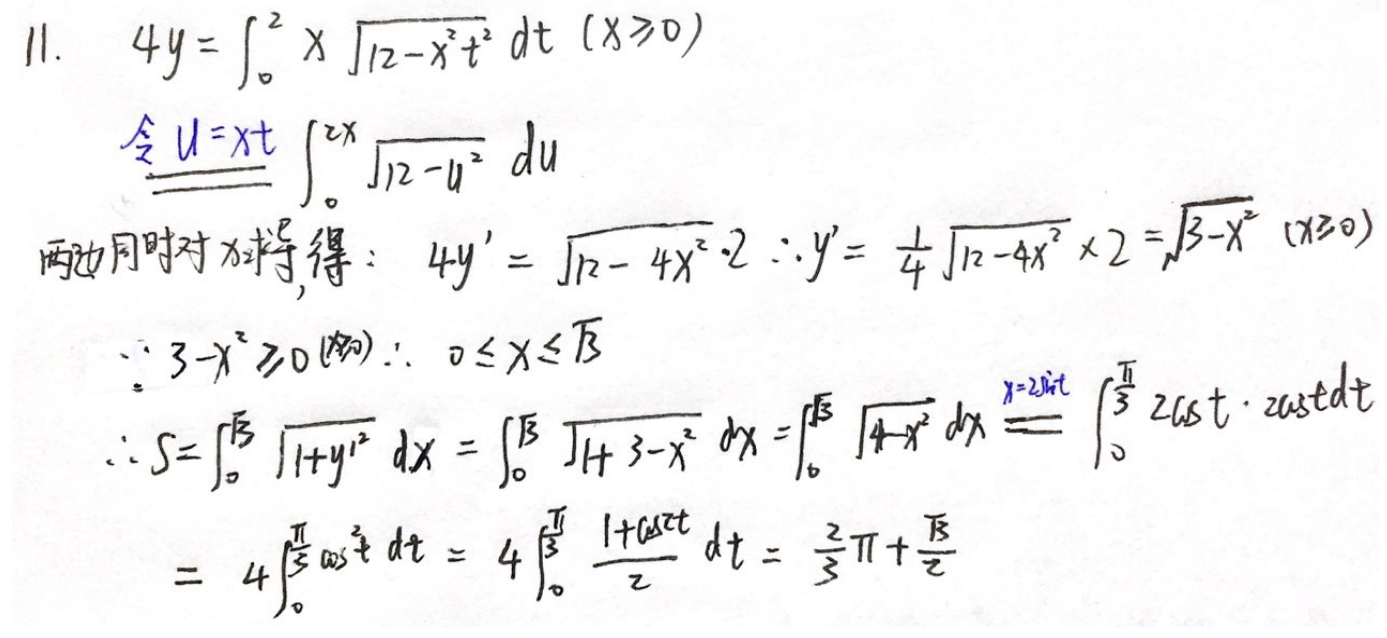
答案: 2 π 3 + 3 2 \dfrac{2π}{3}+\dfrac{\sqrt{3}}{2} 32π+23
三角换元
有根式(如 1 − x 2 \sqrt{1-x²} 1−x2),一般考虑三角换元:令 x = s i n t x=sint x=sint,则 1 − x 2 = 1 − sin 2 t = cos t \sqrt{1-x²}=\sqrt{1-\sin²t}=\cos t 1−x2=1−sin2t=cost
例题1:19年18.
例题2:12年10. ①换元法 ②奇偶性 ③三角代换/定积分几何意义
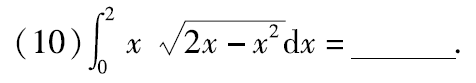
分析:
∫
0
2
x
2
x
−
x
2
d
x
=
∫
0
2
x
1
−
(
x
−
1
)
2
d
x
\int_0^2x\sqrt{2x-x^2}{\rm d}x=\int_0^2x\sqrt{1-(x-1)^2}{\rm d}x
∫02x2x−x2dx=∫02x1−(x−1)2dx
令t=x-1
=
∫
−
1
1
(
t
+
1
)
1
−
t
2
d
t
=
∫
−
1
1
t
1
−
t
2
d
t
+
∫
−
1
1
1
−
t
2
d
t
=
=\int_{-1}^1(t+1)\sqrt{1-t^2}{\rm d}t=\int_{-1}^1t\sqrt{1-t^2}{\rm d}t+\int_{-1}^1\sqrt{1-t^2}{\rm d}t=
=∫−11(t+1)1−t2dt=∫−11t1−t2dt+∫−111−t2dt=(奇偶性)
2
∫
0
1
1
−
t
2
d
t
2\int_0^1\sqrt{1-t^2}{\rm d}t
2∫011−t2dt
①定积分几何意义: 2 ∫ 0 1 1 − t 2 d t = 2 × π × 1 2 4 = π 2 2\int_0^1\sqrt{1-t^2}{\rm d}t=2×\dfrac{π×1^2}{4}=\dfrac{π}{2} 2∫011−t2dt=2×4π×12=2π
②三角代换:令t=sinθ, 2 ∫ 0 1 1 − t 2 d t = 2 ∫ 0 π 2 c o s θ ⋅ c o s θ d θ = 2 ∫ 0 π 2 c o s 2 θ d θ = 2\int_0^1\sqrt{1-t^2}{\rm d}t=2\int_0^{\frac{π}{2}}cosθ·cosθ{\rm d}θ=2\int_0^{\frac{π}{2}}cos^2θ{\rm d}θ= 2∫011−t2dt=2∫02πcosθ⋅cosθdθ=2∫02πcos2θdθ=(点火公式) = 2 × 1 2 × π 2 = π 2 =2×\dfrac{1}{2}×\dfrac{π}{2}=\dfrac{π}{2} =2×21×2π=2π
答案: π 2 \dfrac{π}{2} 2π
3.分部积分
分部积分公式、原则
1.分布积分公式: ∫ u v ′ d x = ∫ u d v = u v − ∫ v d u = u v − ∫ v u ′ d x \int uv'dx=\int udv=uv-\int vdu=uv-\int vu'dx ∫uv′dx=∫udv=uv−∫vdu=uv−∫vu′dx
2.分部积分原则:提到后面的v的顺序:三指幂对反 (反对幂指三是指u的优先级)
表格法
表格法适用于求3种不定积分:幂×对、幂×三角、三角×对
1.
∫
x
n
⋅
e
α
x
d
x
\int x^n·e^{αx}dx
∫xn⋅eαxdx
2.
∫
x
n
⋅
s
i
n
a
x
\int x^n·sinax
∫xn⋅sinax
3.
∫
s
i
n
x
⋅
e
α
x
\int sinx·e^{αx}
∫sinx⋅eαx
2.求法:
上面u微分,下面v积分

例题1:求
∫
e
x
c
o
s
x
d
x
\int e^xcosxdx
∫excosxdx

含变限积分f(x)的定积分:用分部积分凑f(x)的导数
分部积分的一个重要特点:能凑出导数
例题1:13年15. 求含变限积分的定积分:用分部积分凑导数

答案: − 4 l n 2 + 8 − 2 π -4ln2+8-2π −4ln2+8−2π
4.区间再现
1.区间再现是什么:令
x
=
a
+
b
−
t
x=a+b-t
x=a+b−t,则
f
(
x
)
=
f
(
a
+
b
−
t
)
f(x)=f(a+b-t)
f(x)=f(a+b−t),则
∫
a
b
f
(
x
)
d
x
=
∫
a
b
f
(
a
+
b
−
t
)
d
t
\int_a^bf(x)dx=\int_a^bf(a+b-t)dt
∫abf(x)dx=∫abf(a+b−t)dt
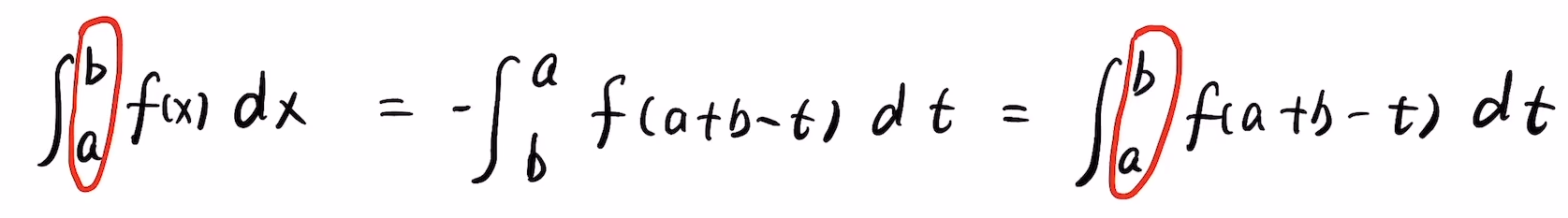
2.应用场景:区间再现通常用的情况:①积分区间不变的变量代换 ②被积函数的原函数不易求出
例题1:
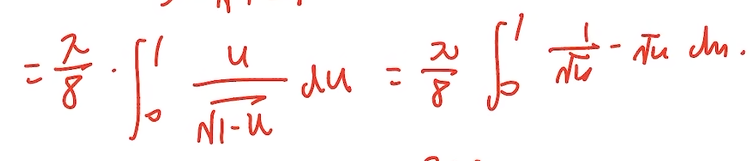
区间再现,令t=1-u (令u=1-t)
例题2:
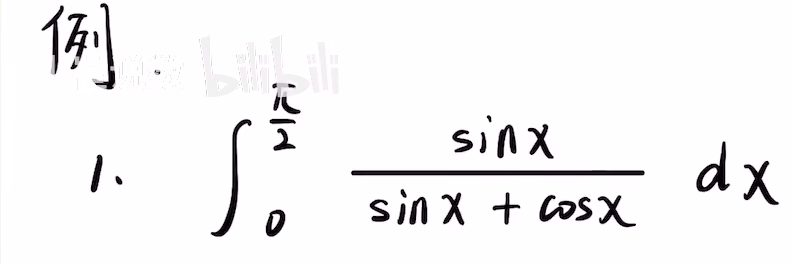
答案:

5.求定积分的公式
1.牛顿-莱布尼茨公式
∫ a b f ( x ) d x = F ( b ) − F ( a ) = F ( x ) ∣ a b \int_a^bf(x){\rm d}x=F(b)-F(a)=F(x)|_a^b ∫abf(x)dx=F(b)−F(a)=F(x)∣ab
2.点火公式/华里士公式/Wallis公式:

n为奇数时,最后一项是
2
3
\dfrac{2}{3}
32
n为偶数时,最后两项是 1 2 ⋅ π 2 \dfrac{1}{2}·\dfrac{π}{2} 21⋅2π
函数图像生成网站
可以发现, s i n n x sin^nx sinnx 的一个蘑菇的宽度(一股的跨度)一直是π。n为偶数时是偶函数,n为奇数时是奇函数。
4.变限积分
1.变限积分求导
变限积分求导公式: d d x ∫ a φ ( x ) f ( t ) d t = f [ φ ( x ) ] φ ′ ( x ) \dfrac{\rm d}{{\rm d}x}\int_a^{φ(x)}f(t)dt=f[φ(x)]φ'(x) dxd∫aφ(x)f(t)dt=f[φ(x)]φ′(x)
用积分上限替换被积变量,并对积分上限再求一次导。
注意,替换时要求被积变量是干净的,不含其他字母的,否则要分两项或者换元。
①若仅仅是加减法,则可以分两项
②若是幂、括号内的自变量不干净,一般需要换元
例题1:23李林六套卷(五)11. 括号内自变量不干净:换元
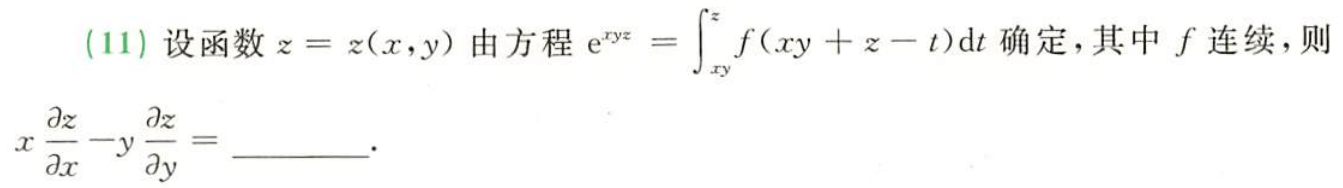
分析:①换元(换元要换上下限) ②区间变换

答案:0
例题2:20年12. 积分上限函数、二元混合偏导

分析:
∂
f
∂
y
=
e
x
(
x
y
)
2
⋅
x
=
x
e
x
3
y
2
\dfrac{∂f}{∂y}=e^{x(xy)^2}·x=xe^{x^3y^2}
∂y∂f=ex(xy)2⋅x=xex3y2
∂ 2 f ∂ y ∂ x = ∂ ( ∂ f ∂ y ) ∂ x = e x 3 y 2 + x e x 3 y 2 ⋅ y 2 3 x 2 = ( 1 + 3 x 3 y 2 ) e x 3 y 2 \dfrac{∂^2f}{∂y∂x}=\dfrac{∂(\dfrac{∂f}{∂y})}{∂x}=e^{x^3y^2}+xe^{x^3y^2}·y^23x^2=(1+3x^3y^2)e^{x^3y^2} ∂y∂x∂2f=∂x∂(∂y∂f)=ex3y2+xex3y2⋅y23x2=(1+3x3y2)ex3y2
∂ 2 f ∂ y ∂ x ∣ ( 1 , 1 ) = ( 1 + 3 x 3 y 2 ) e x 3 y 2 ∣ ( 1 , 1 ) = ( 1 + 3 ) e = 4 e \dfrac{∂^2f}{∂y∂x}|_{(1,1)}=(1+3x^3y^2)e^{x^3y^2}|_{(1,1)}=(1+3)e=4e ∂y∂x∂2f∣(1,1)=(1+3x3y2)ex3y2∣(1,1)=(1+3)e=4e
答案:4e
例题3:10年16.
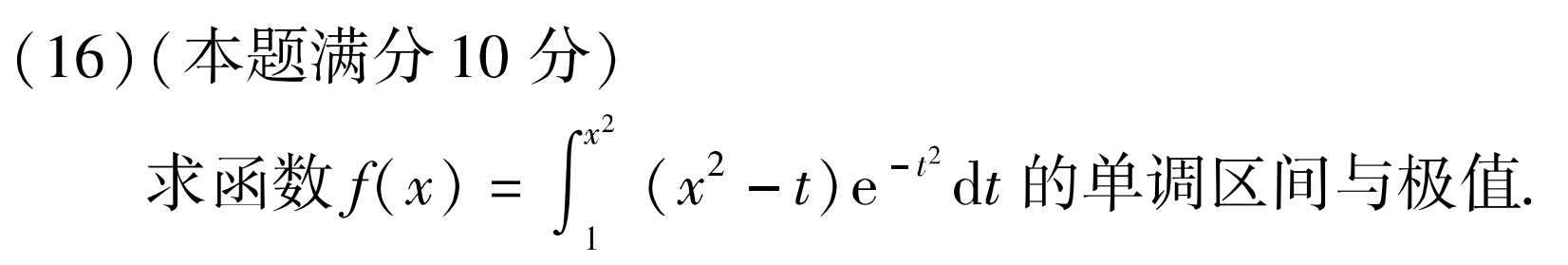
2.变限积分的连续性与可导性

例题1:23李林六套卷(一)2.

分析:
(法一)变限积分的可导性
f在除x₀点处均连续,则
若x₀点连续、可去间断点,则f的变限积分可导
若x₀点跳跃间断点,则f的变限积分连续不可导
f是分段函数,a决定了f是连续的还是跳跃间断点,因此f的变限积分的可导性取决于a
(法二)导数定义
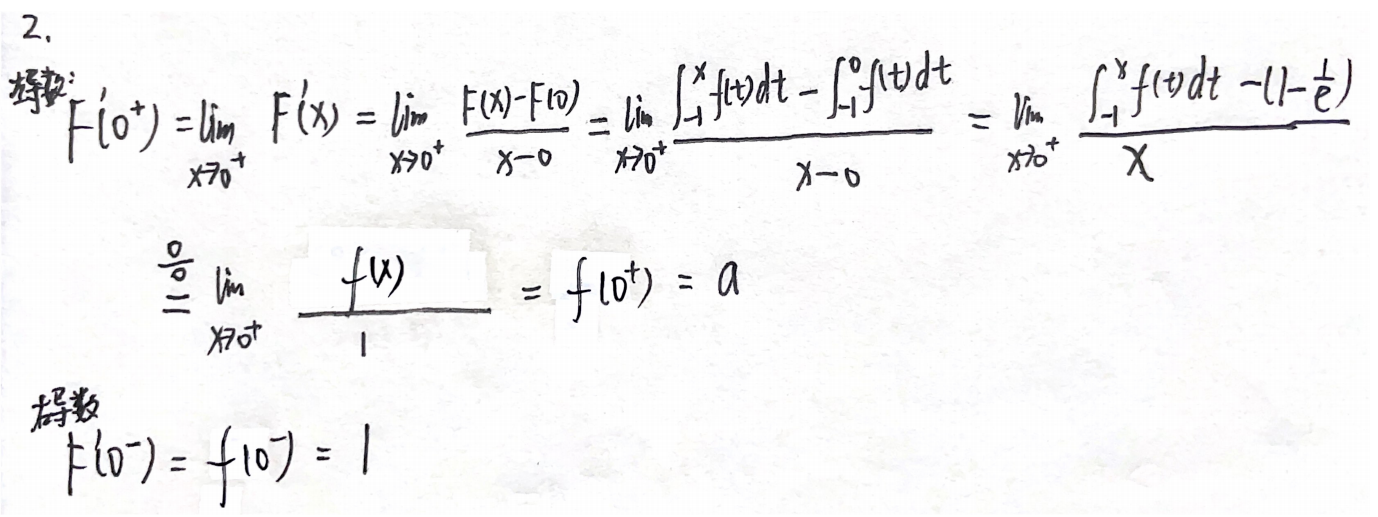
答案:D
5. 广义积分/反常积分
1.无穷限的广义积分
广义积分的计算
跳转链接
2.无界函数的反常积分 / 瑕积分
瑕积分的计算不难,要仔细地分离出有限部分和带瑕点的部分,后者用极限求出,常用洛必达。注意不要抄错。
例题1:23李林六套卷(三)12.
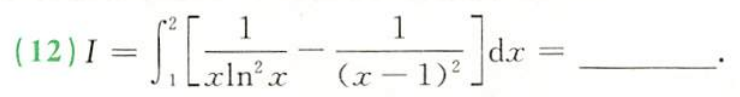
答案:

3.反常积分的审敛法
1.极限审敛法
反常积分收敛:瑕点 p<1,无穷p>1


2.比较审敛法
同济上册P262-267

例题1:16年1.

分析:反常积分收敛:瑕点 p<1,无穷p>1
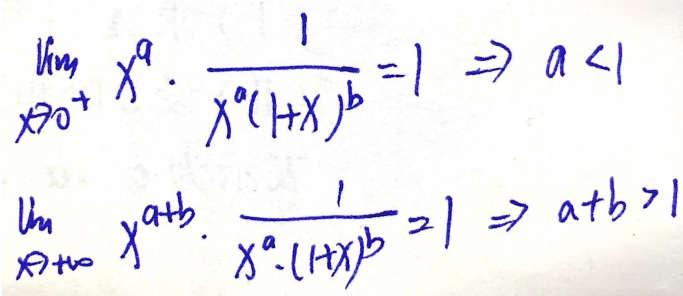
答案:C
例题2:10年3. 无界函数的反常积分审敛法

答案:D
6.Γ函数
Γ ( n + 1 ) = ∫ 0 + ∞ x n ⋅ e − x d x = n ! Γ(n+1)=\int_0^{+∞}x^n·e^{-x}dx=n! Γ(n+1)=∫0+∞xn⋅e−xdx=n!
Ch6.定积分应用
定积分的几何应用
1.平面图形的面积
2.旋转体体积
3.平面曲线的弧长
注意:若是f(x)带有sinx,则需要分区间讨论,无穷多个区间,需要用无穷级数。而不能直接在[0,+∞)上积分
例题1:19年17.
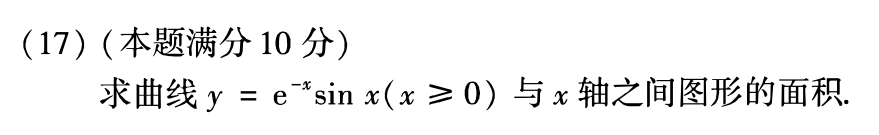
分析:
答案: 1 2 + 1 e π − 1 \dfrac{1}{2}+\dfrac{1}{e^π-1} 21+eπ−11
例题2:23李林四(四)11.

分析:

答案: π 5 ( 1 − e − 2 π ) \dfrac{π}{5(1-e^{-2π})} 5(1−e−2π)π
定积分的物理应用
0.速度与路程
面积是路程
例题1:17年4.

分析:
①交点是速度相等
②积分面积相等才是路程相等,注意甲多出来10m的路程
∴t=25时,S=10+10-20=0
答案:C
1.变力做功
2.水压力
例题1:23李林六套卷(四)12.

答案:
3.引力
Ch7.微分方程
跳转此处:https://blog.csdn.net/Edward1027/article/details/127150223