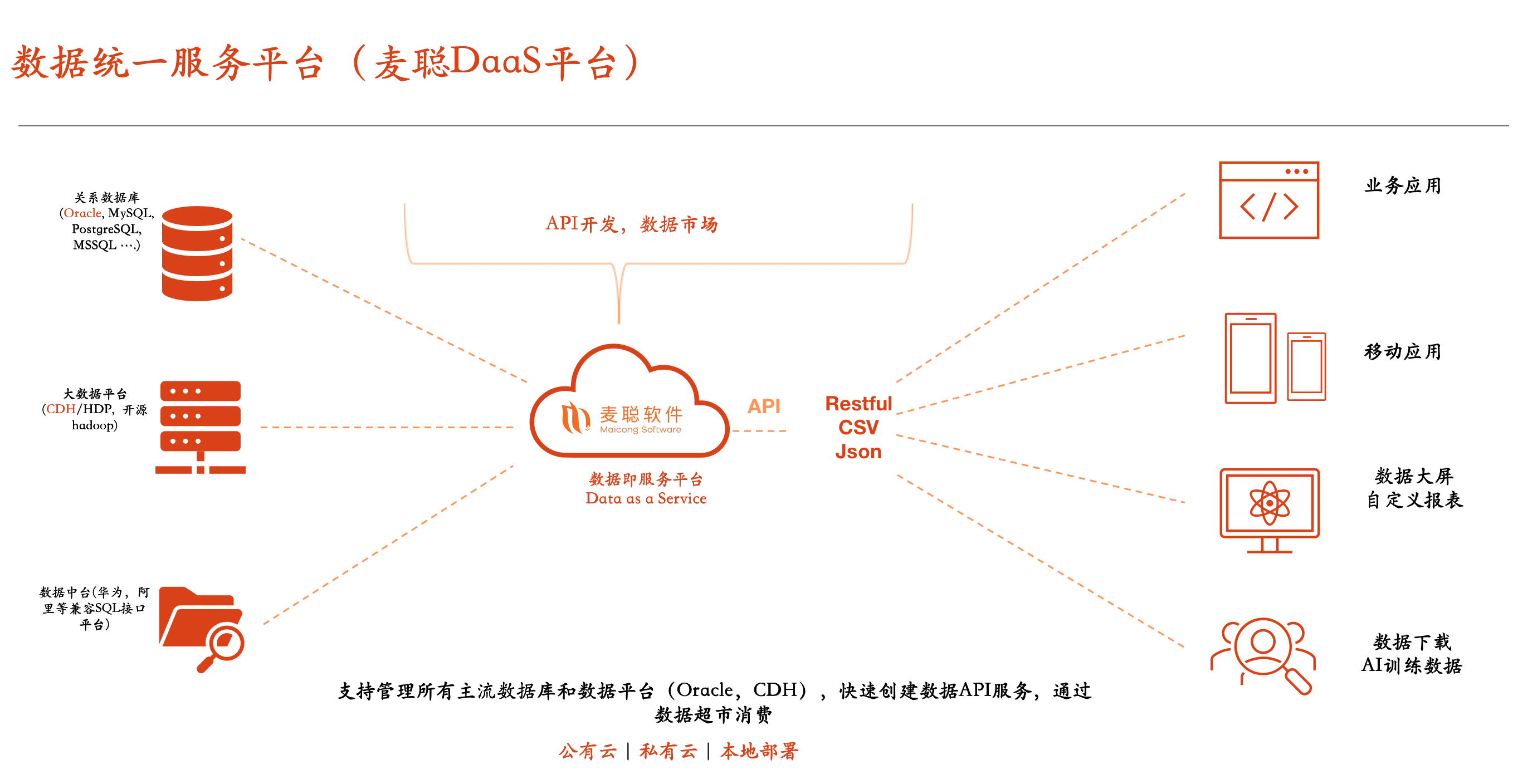
题目描述

方法一：哈希表

C++版本

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        unordered_set<ListNode*> visited;
        while(head != NULL) {
            if(visited.count(head))		// 若第一次遇到之前遍历过的链表，则为环的入口
                return head;
            visited.insert(head);		// 记录遍历过的链表
            head = head->next;
        }

        return NULL;
    }
};

Python版本

通过集合来实现

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def detectCycle(self, head: ListNode) -> ListNode:
        visited = set()                
        while head != None :                        
            if id(head) in visited :              
                return head            
            visited.add(id(head))
            head = head.next                        

        return None

id() 函数返回对象的唯一标识符，标识符是一个整数。

时间复杂度 $O (n)$
空间复杂度 $O (n)$

方法二：快慢指针

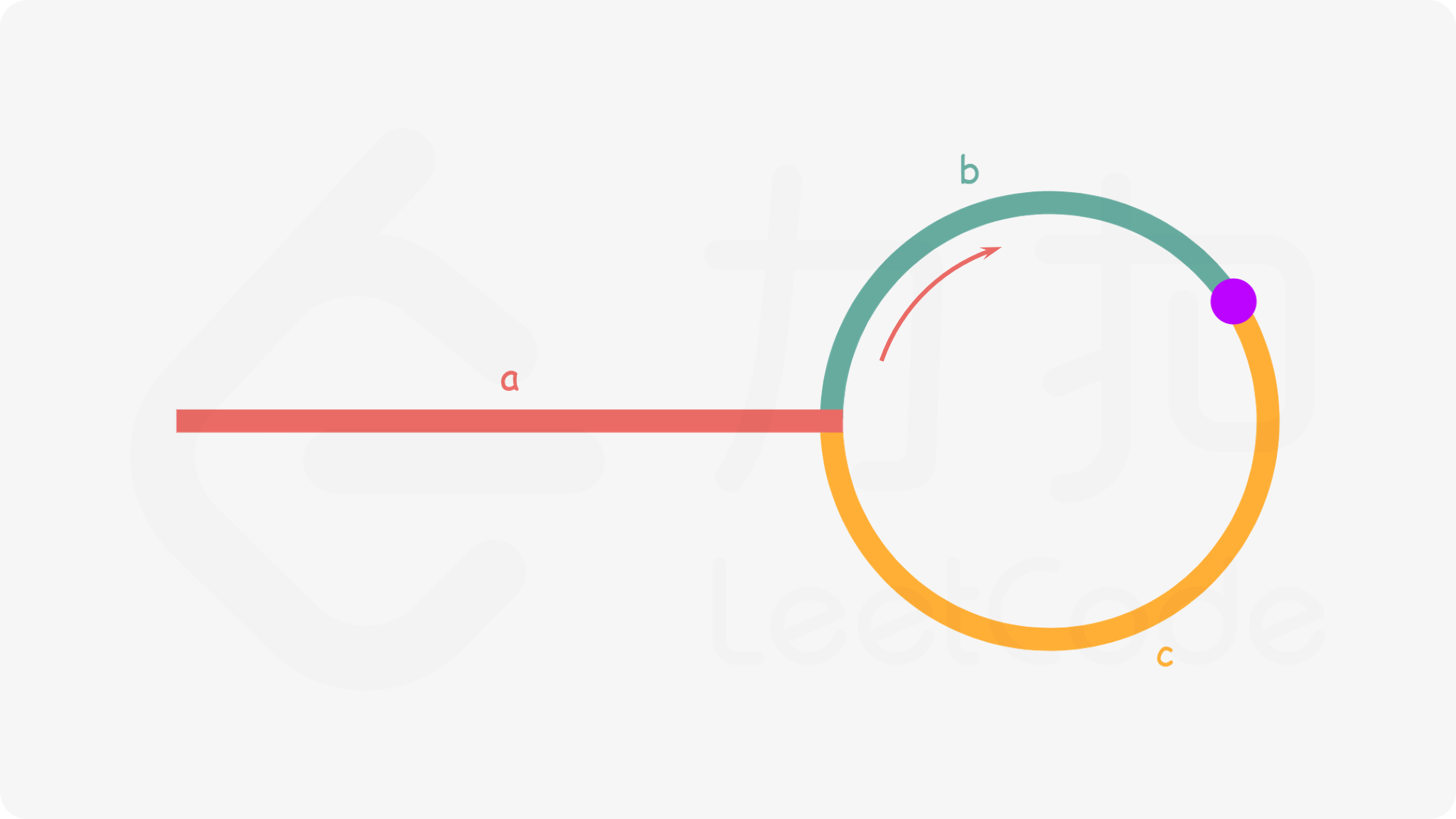
slow指针走过的为a+b，fast指针走过的为a+b+n(b+c)，其中n为fast指针走过的圈数。
因为fast一次走两步，slow一次走一步，那么fast就会相对于slow以速度为1步进行运动，那么总有一次二者会相遇。

根据二者速度关系可列等式 $2 * (a + b) = (a + b) + n (b + c)$ ，可得 $a = n (b + c) - b$ ，即 $a = (n - 1) (b + c) + c$ ，由该公式可得，走过距离a等于走n-1圈环的距离再加上从相遇点走过距离c。

因此，若想得到入口点，可让一个指针从头节点出发，另一个指针从相遇点出发。两者必然会在某一时刻，再入口点相遇。

C++版本

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* fast = head;
        ListNode* slow = head;

        while(fast != NULL && fast->next != NULL){
            fast = fast->next->next;
            slow = slow->next;
            if(fast == slow){		// 找到相遇点
                ListNode* ptr = head;	// 设置一个从头结点出发的指针
                while(ptr != slow){		// 当从头结点出发的结点和从相遇点出发的结点相遇时，则为入口点
                    ptr = ptr->next;
                    slow = slow->next;
                }
                return ptr;
            }
        }
        return NULL;
    }
};

Python版本

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def detectCycle(self, head: ListNode) -> ListNode:
        fast, slow = head, head

        while fast != None and fast.next != None :
            fast = fast.next.next
            slow = slow.next
            if fast == slow :
                ptr = head
                while slow != ptr :
                    slow = slow.next
                    ptr = ptr.next
                return ptr

        return None