





import java.util.Arrays;
/*
* 弗洛伊德算法
* 1.和迪杰斯特拉算法一样,弗洛伊德算法也是一种用于寻找给定的加权图中顶点间最短路径的算法
* 2.迪杰斯特拉算法用于计算图中某一顶点到其他顶点的最短路径
* 弗洛伊德算法计算图中各个顶点之间的最短路径
* 3.迪杰斯特拉算法通过选定的被访问顶点,求出从出发访问顶点到其他顶点的最短路径
* 弗洛伊德算法中每一个顶点都是出发访问点,求出从每一个顶点到其他顶点的最短路径
*
* 过程
* 1.设置顶点vi到顶点vk的最短路径已知为Lik,顶点vk到vj的最短路径已知为Lkj,顶点vi到vj的路径为Lij
* 则vi到vj的最短路径为:min((Lik+Lkj),Lij),vk取值为图中所有顶点,则可获得vi到vj的最短路径
* 2.vi到vk的最短路径Lik或vk到vj的最短路径Lkj,以同样方式获得
*
* 步骤
* 1.第一轮循环,把A(下标为0)作为中间顶点,更新距离和前驱关系
* 2.重复执行....
*
* 应用——最短路径问题
*/
public class Floyd {
public static void main(String[] args) {
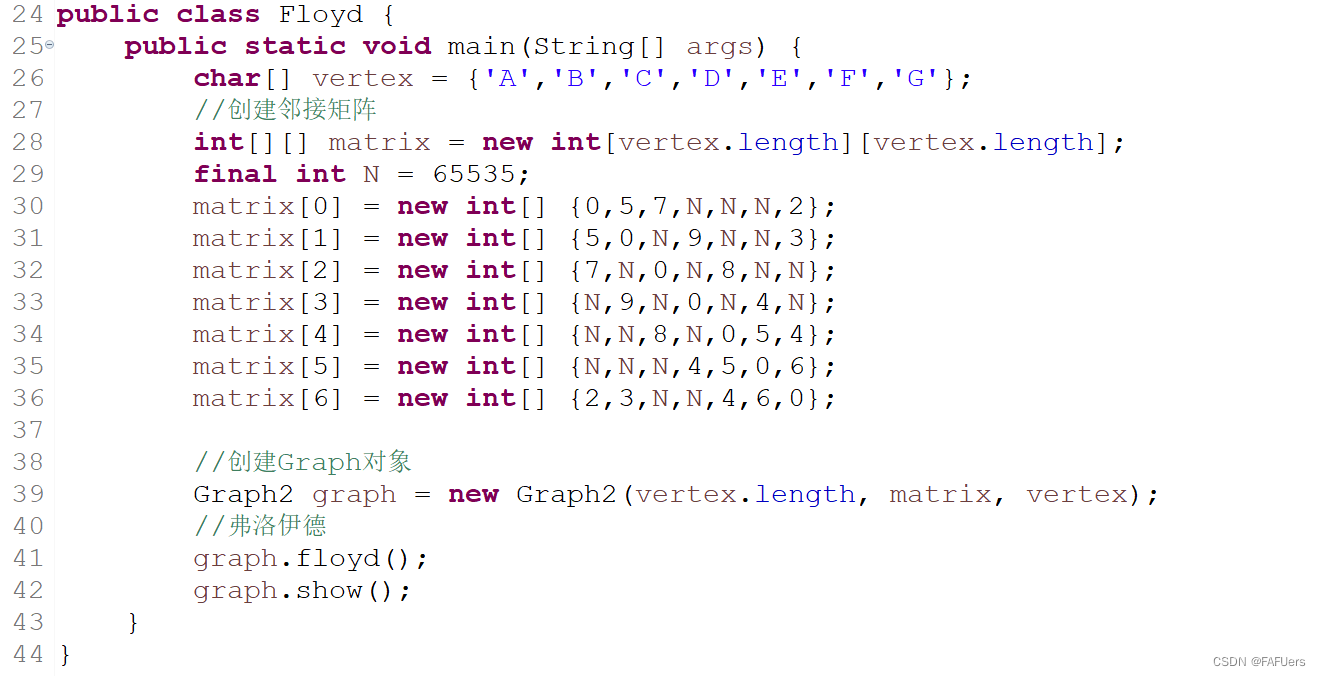
char[] vertex = {'A','B','C','D','E','F','G'};
//创建邻接矩阵
int[][] matrix = new int[vertex.length][vertex.length];
final int N = 65535;
matrix[0] = new int[] {0,5,7,N,N,N,2};
matrix[1] = new int[] {5,0,N,9,N,N,3};
matrix[2] = new int[] {7,N,0,N,8,N,N};
matrix[3] = new int[] {N,9,N,0,N,4,N};
matrix[4] = new int[] {N,N,8,N,0,5,4};
matrix[5] = new int[] {N,N,N,4,5,0,6};
matrix[6] = new int[] {2,3,N,N,4,6,0};
//创建Graph对象
Graph2 graph = new Graph2(vertex.length, matrix, vertex);
//弗洛伊德
graph.floyd();
graph.show();
}
}
class Graph2{
private char[] vertex;//存放顶点数组
private int[][] dis;//保存从各个顶点出发到其他顶点的距离
private int[][] pre;//保存到达目标顶点的前驱顶点
//构造器
//length:大小,matrix:邻接矩阵,vertex:顶点数组
public Graph2(int length,int[][] matrix,char[] vertex) {
this.vertex = vertex;
this.dis = matrix;
this.pre = new int[length][length];
//对pre数组初始化(存放的是前驱顶点下标)
for(int i = 0;i < length;i++) {
Arrays.fill(pre[i],i);
}
}
//显示pre数组和dis数组
public void show() {
char[] vertex = {'A','B','C','D','E','F','G'};
for(int k = 0;k < dis.length;k++) {
//输出pre数组的一行
for(int i = 0;i < dis.length;i++) {
System.out.print(vertex[pre[k][i]] + " ");
}
System.out.println();
//输出dis数组的一行
for(int i = 0;i < dis.length;i++) {
System.out.print("(" + vertex[k] + "到" + vertex[i] + "的最短路径:" + dis[k][i]+")");
}
System.out.println();
System.out.println();
}
}
//弗洛伊德算法
public void floyd() {
int len = 0;//保存距离
//对中间顶点遍历,k为中间顶点下标
for(int k = 0;k < dis.length;k++) {
//从i顶点开始出发,经过中间顶点
for(int i = 0;i < dis.length;i++) {
//到达j顶点
for(int j = 0;j < dis.length;j++) {
len = dis[i][k] + dis[k][j];//从i顶点出发,经过k中间顶点,到达j顶点的距离
if (len < dis[i][j]) {
dis[i][j] = len;//更新距离
pre[i][j] = pre[k][j];//更新前驱顶点
}
}
}
}
}
}
/*
* 马踏棋盘算法(骑士周游问题
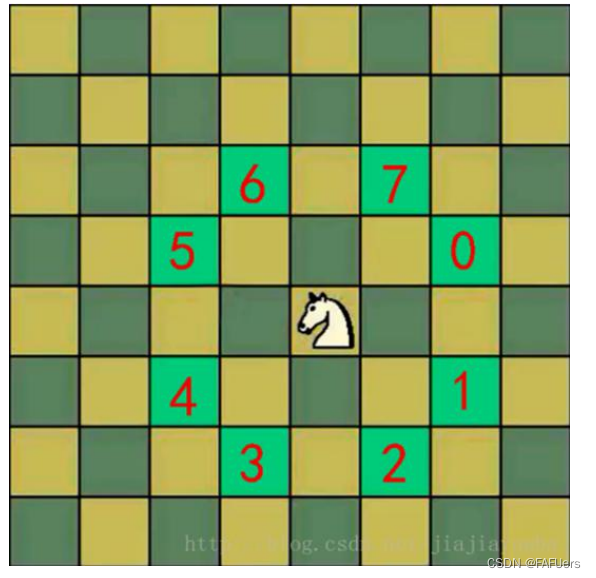
* 将马随机放在国际象棋的8*8棋盘的某个方格中,马按规则(走日字)进行移动
* 要求每个方格只进入一次,走遍棋盘上全部64个方格
*
* 1.马踏棋盘问题实际上是图的深度优先搜索(DFS)的应用
* 2.如果使用回溯(深度优先搜索)来解决,加入马走了x个点,发现已走到尽头
* 就只能回退,查看其他路径
*
* 思路
* 1.创建棋盘chessBoard,二维数组
* 2.将当前位置设置为已经访问,根据当前位置,计算马还能走哪些位置,
* 并放入一个集合中(ArrayList),最多有8个位置
* 每走一步,就step+1
* 3.遍历ArrayList中存放的所有位置,看看哪个能走通
* 走通就继续,走不通回溯
* 4.判断马是否完成了任务,使用step和应该走的步数比较,如没达到,棋盘置0
*
* //不同的走法(策略),得到不同的结果,效率也会有影响
*
* 使用贪心算法进行优化
* 1.获取当前位置可以走的下一个位置的集合
* ArrayList<Point> ps = next(new Point(column, row));
* 2.对ps中所有point的下一步的所有集合的数目,通过非递减排序
*/
import java.awt.Point;
import java.util.ArrayList;
import java.util.Comparator;
public class HorseChessBoard {
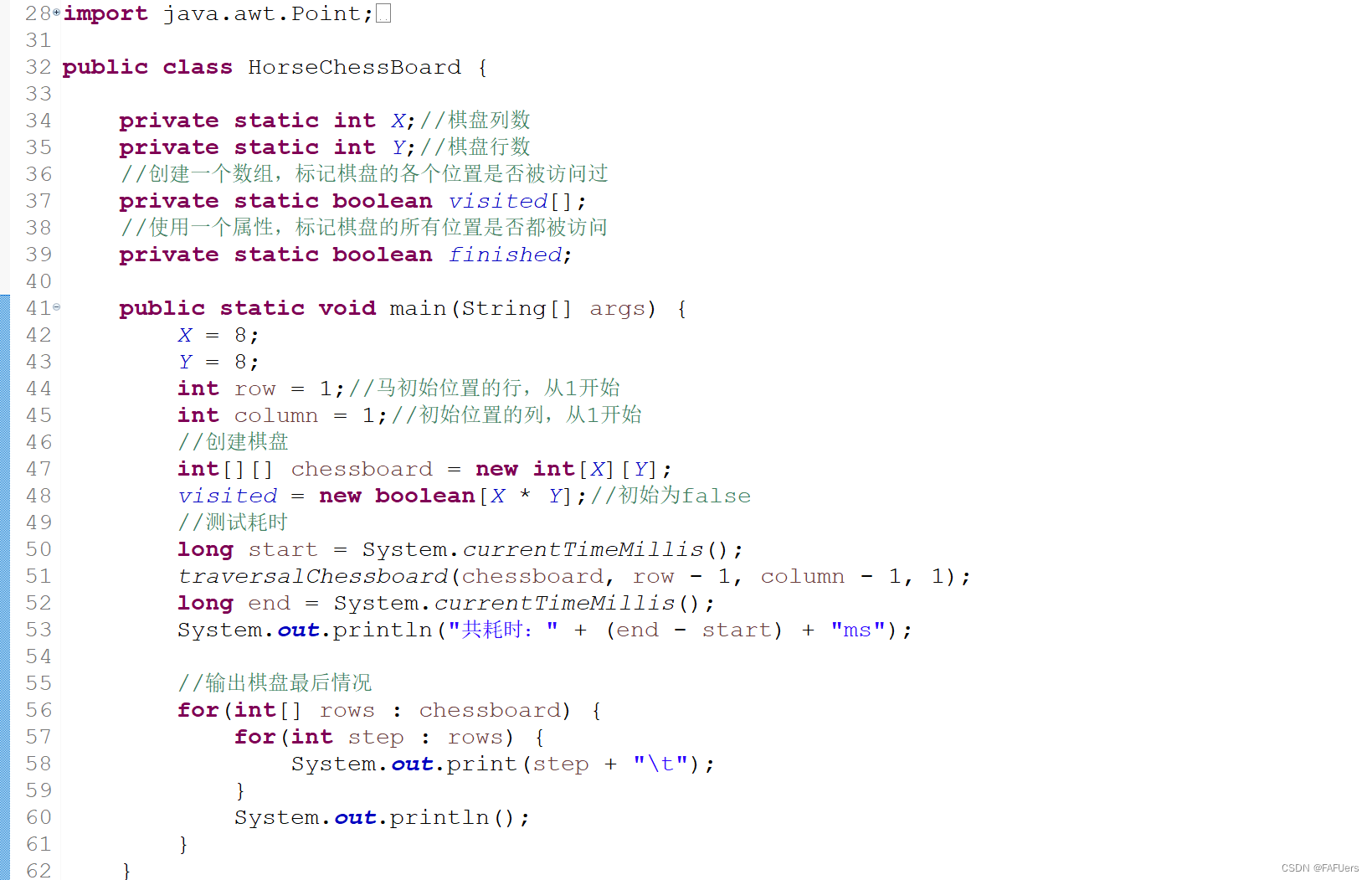
private static int X;//棋盘列数
private static int Y;//棋盘行数
//创建一个数组,标记棋盘的各个位置是否被访问过
private static boolean visited[];
//使用一个属性,标记棋盘的所有位置是否都被访问
private static boolean finished;
public static void main(String[] args) {
X = 8;
Y = 8;
int row = 1;//马初始位置的行,从1开始
int column = 1;//初始位置的列,从1开始
//创建棋盘
int[][] chessboard = new int[X][Y];
visited = new boolean[X * Y];//初始为false
//测试耗时
long start = System.currentTimeMillis();
traversalChessboard(chessboard, row - 1, column - 1, 1);
long end = System.currentTimeMillis();
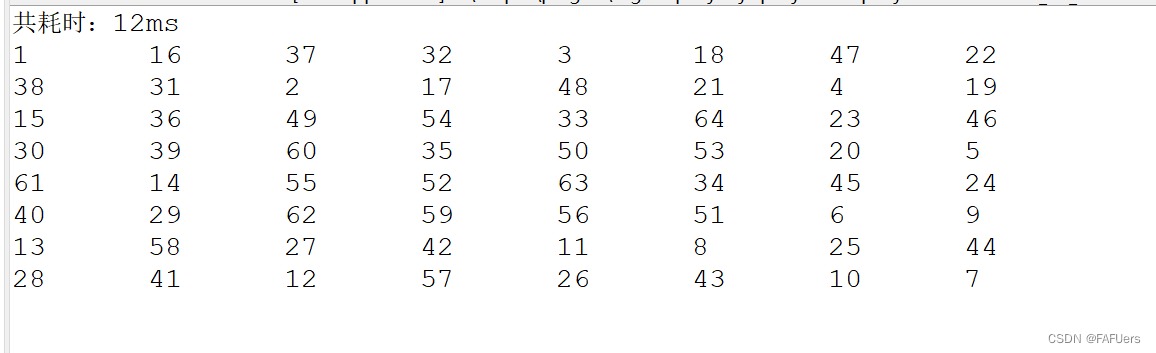
System.out.println("共耗时:" + (end - start) + "ms");
//输出棋盘最后情况
for(int[] rows : chessboard) {
for(int step : rows) {
System.out.print(step + "\t");
}
System.out.println();
}
}
//马踏棋盘算法
//chessbo:棋盘,row:当前位置的行(从0开始)column:当前位置的列(从0开始)step:第几步,初始位置为第一步
public static void traversalChessboard(int[][] chessboard,int row,int column,int step) {
chessboard[row][column] = step;
//row=4,X=8,column=4,当前位置为4*8+4=36
visited[row * X + column] = true;//标记已访问
//获取当前位置的下一个位置集合
ArrayList<Point> ps = next(new Point(column, row));
//对ps排序
sort(ps);
//遍历ps
while(!ps.isEmpty()) {
Point p = ps.remove(0);//取出下一个可以走的位置
//判断是否已经访问过
if (!visited[p.y * X + p.x]) {//说明还没访问过
traversalChessboard(chessboard, p.y, p.x, step + 1);
}
}
//判断马是否完成了任务,使用step和应该走的步数比较,如没达到,棋盘置0
//step < X * Y 成立情况有两种
//1.棋盘到目前位置,仍然没有走完
//2.棋盘处于一个回溯过程
if (step < X * Y && !finished) {
chessboard[row][column] = 0;
visited[row * X + column] = false;
}else {
finished = true;
}
}
//根据当前位置(Point对象),计算马还能走哪些位置,并放入一个集合中(ArrayList)
//curPoint:当前位置
public static ArrayList<Point> next(Point curPoint){
//创建ArrayList
ArrayList<Point> ps = new ArrayList<Point>();
//创建一个Point
Point p1 = new Point();
//最多有8个位置
//判断马儿能不能往左移动两列,往上移动一行
if ((p1.x = curPoint.x - 2) >= 0 && (p1.y = curPoint.y - 1) >= 0) {
ps.add(new Point(p1));
}
//判断马儿能不能往左移动一列,往上移动两行
if ((p1.x = curPoint.x - 1) >= 0 && (p1.y = curPoint.y - 2) >= 0) {
ps.add(new Point(p1));
}
//判断马儿能不能往右移动一列,往上移动两行
if ((p1.x = curPoint.x + 1) < X && (p1.y = curPoint.y - 2) >= 0) {
ps.add(new Point(p1));
}
//判断马儿能不能往右移动两列,往上移动一行
if ((p1.x = curPoint.x + 2) < X && (p1.y = curPoint.y - 1) >= 0) {
ps.add(new Point(p1));
}
//判断马儿能不能往右移动两列,往下移动一行
if ((p1.x = curPoint.x + 2) < X && (p1.y = curPoint.y + 1) < Y) {
ps.add(new Point(p1));
}
//判断马儿能不能往右移动一列,往下移动两行
if ((p1.x = curPoint.x + 1) < X && (p1.y = curPoint.y + 2) < Y) {
ps.add(new Point(p1));
}
//判断马儿能不能往左移动一列,往下移动两行
if ((p1.x = curPoint.x - 1) >= 0 && (p1.y = curPoint.y + 2) < Y) {
ps.add(new Point(p1));
}
//判断马儿能不能往左移动两列,往下移动一行
if ((p1.x = curPoint.x - 2) >= 0 && (p1.y = curPoint.y + 1) < Y) {
ps.add(new Point(p1));
}
return ps;
}
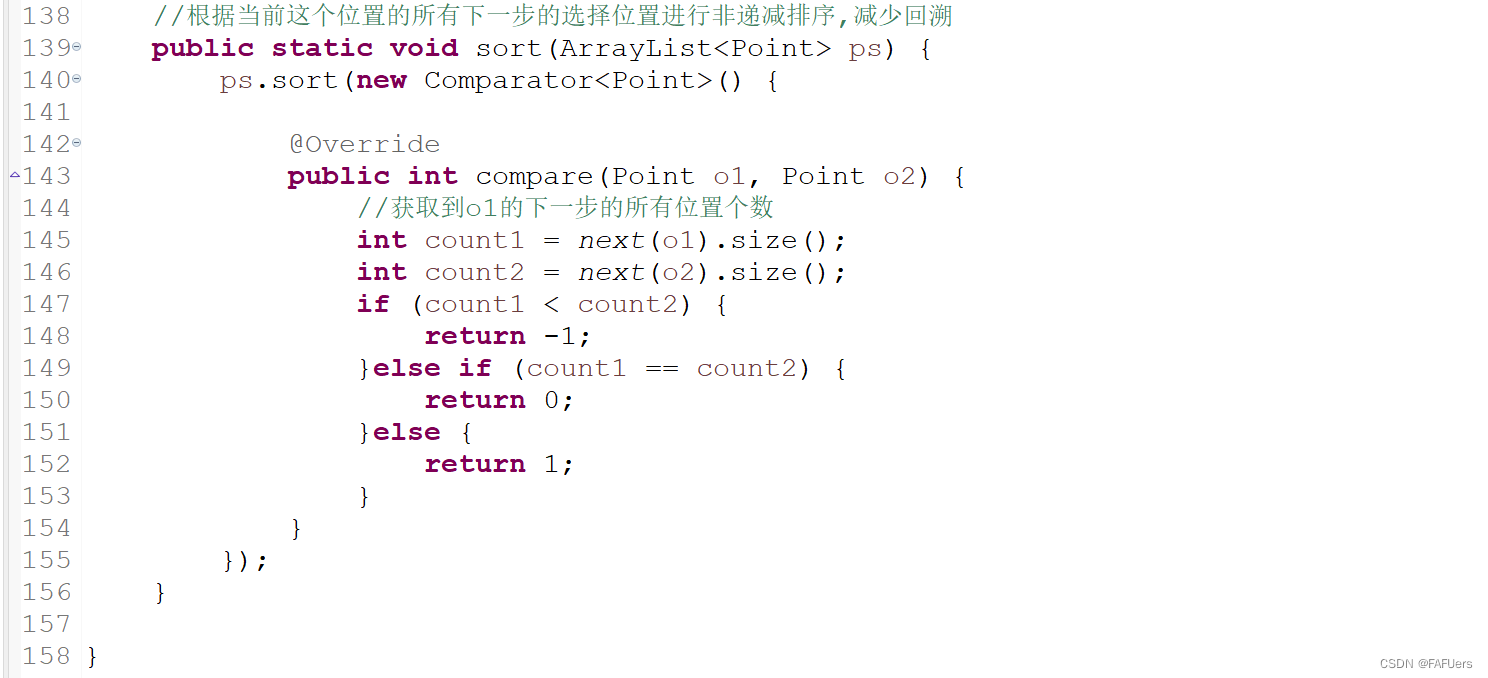
//根据当前这个位置的所有下一步的选择位置进行非递减排序,减少回溯
public static void sort(ArrayList<Point> ps) {
ps.sort(new Comparator<Point>() {
@Override
public int compare(Point o1, Point o2) {
//获取到o1的下一步的所有位置个数
int count1 = next(o1).size();
int count2 = next(o2).size();
if (count1 < count2) {
return -1;
}else if (count1 == count2) {
return 0;
}else {
return 1;
}
}
});
}
}