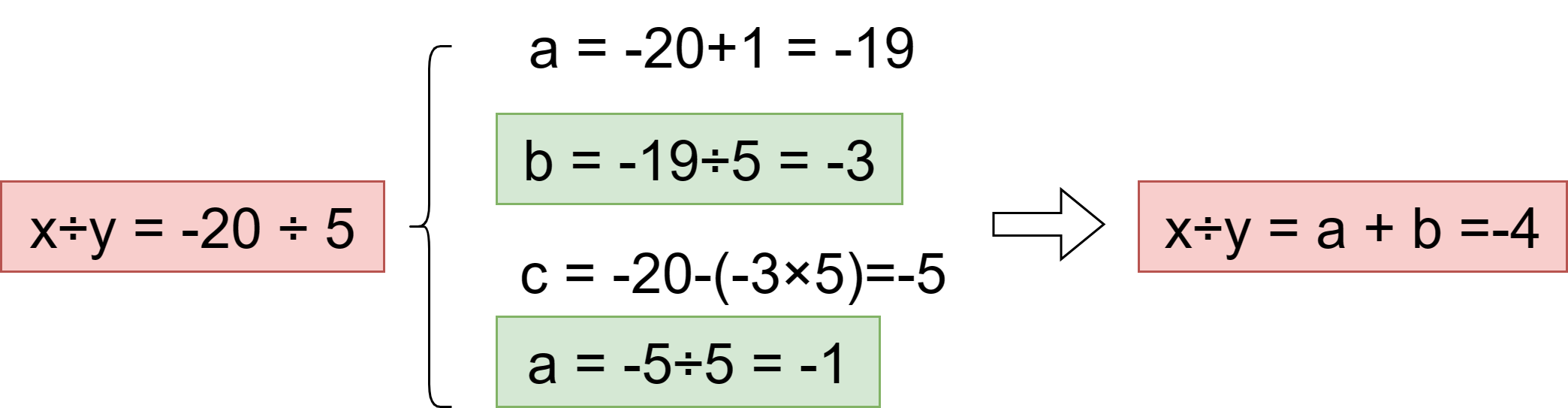文章目录
- 🚀前言
- 🚀异或运算以及与运算
- 🚀加法的实现
- 🚀减法的实现
- 🚀乘法的实现
- 🚀除法的实现
🚀前言
这也是阿辉开的新专栏,知识将会很零散不成体系,不过绝对干货满满,今天这一篇利用位运算实现加减乘除费了阿辉九牛二虎之力,干的很自备饮水😆不多bb,进入今天的学习吧!!!
以下int均为有符号int,所求的加减乘除也是int类型的整型数
严谨 😏
🚀异或运算以及与运算
在写加减乘除之前,先给铁子们介绍一下异或运算以及与运算的其他理解
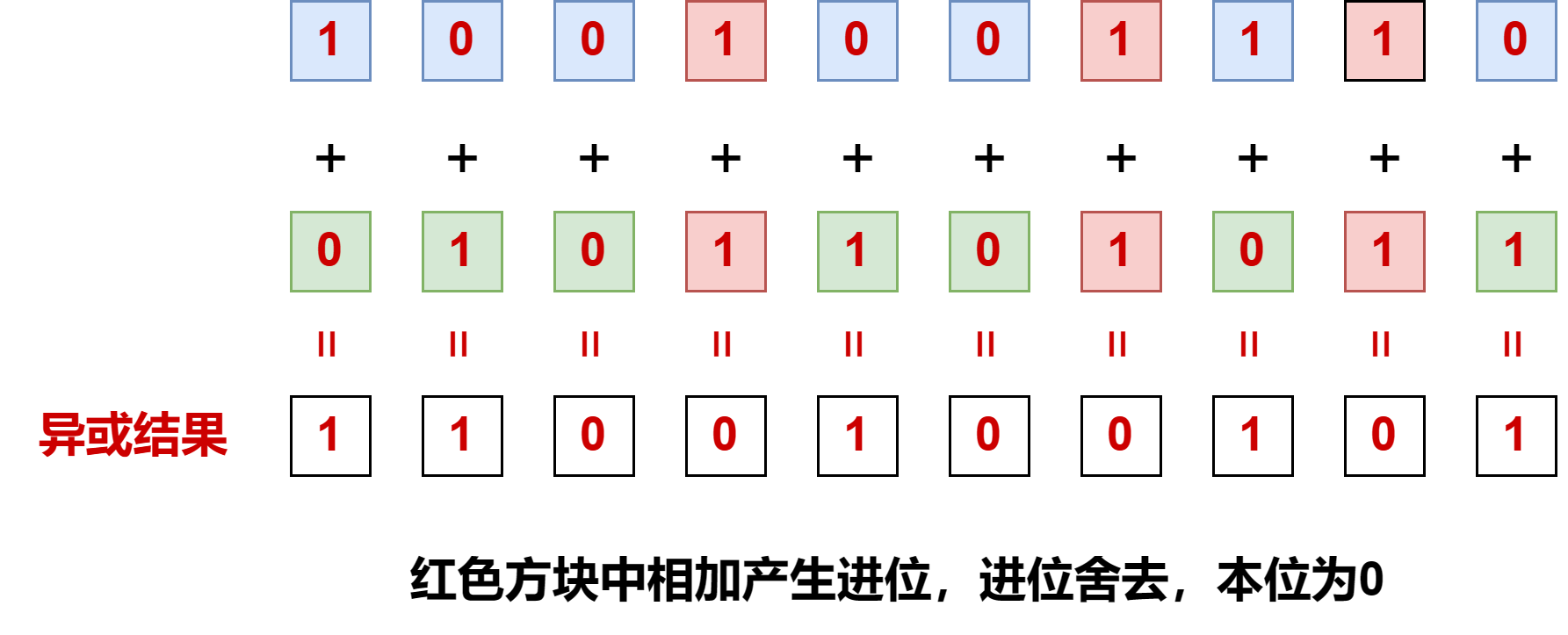
异或运算:也叫无进位相加
这怎么理解呢?
铁子们都知道,异或运算,是二进制位相异为1,相同为0
其实异或运算也可以解释为无进位相加。这是什么意思呢?就是对应的二进制位相加,如果产生进位就将进位舍去。什么是进位呢?对应的二进制位相加为2时就向前进一位,就像我们小时候学的加法一样。而二进制进位后,本位就剩下一个0。而在异或运算中,进位被舍去,所以当两个位都为1时,异或的结果为0;当两个位都为0时,异或的结果也为0;只有一个位为1,另一个位为0时,异或的结果才为1
给铁子们上图解释:
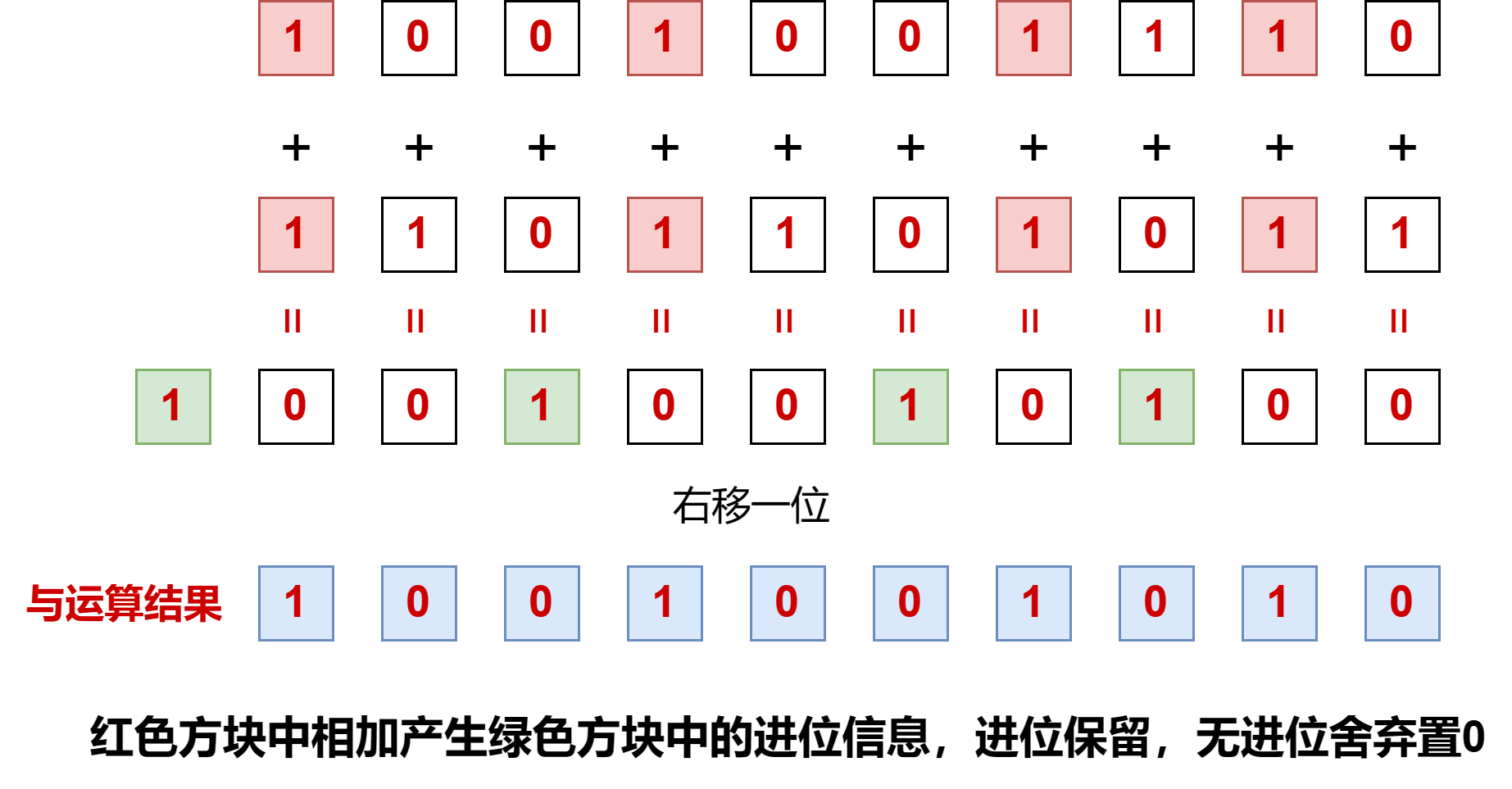
与运算:得到对应二进制位相加的进位信息右移一位后的结果
怎么理解呢?
铁子们都知道,与运算,是两二进制位都为1为1,一个为0就为0
实际上,与运算是得到对应二进制位相加的进位信息右移一位后的结果,怎么理解呢?二进制位相加时产生的进位保留,没有进位舍去直接置0,然后将得到的结果右移一位。
给铁子们上图解释:
🚀加法的实现
有了上述关于异或运算和与运算的新的理解,基于此,我们可以用他们拼凑出加法,怎么拼呢?铁子们接着看👇
根据前面的讲解我们知道,两个数异或运算得到的是两个数相加去掉进位信息后的结果,而两个数与运算得到的是两个数相加保留进位信息右移一位后的结果,铁子们,睁大眼骚操作来了😏,异或运算是去掉进位信息的结果,与运算结果再左移一位(进位信息右移了嘛,再左移回去)是保留进位信息的结果,那两个数异或运算的结果加上两个数与运算再左移一位的结果不就是两个数相加的结果嘛;
铁子们一定会说这不还得在加一遍,有毛用,别急还有更骚的😏😏,两个数的异或运算的结果和与运算左移一位的结果,只要与运算左移一位的结果不为0也就是进位信息不为0,得到的俩个数重复上述操作,直到进位信息为0,异或运算的结果不就是两数相加的结果嘛。铁子们,骚不骚?觉得骚的,记得在评论区给阿辉扣个666 😘
肯定有老铁会说难道进位信息一定会计算到0吗?好问题哈哈哈哈 😜,一定会计算到0,为什么呢?阿辉用图说明,鼠标写的铁子们凑合看一下🙏

异或运算就是把二进制数相加得到如上述不加上蓝色进位信息的结果,然后和进位信息继续异或,直到不在产生进位信息得到相加的结果
如果还有铁子不懂,可以私聊阿辉加个微信,阿辉必给你搞明白,上面进位信息为啥一定会算到0是阿辉自己想的,自认还有点骚,哈哈哈 😁!
下面就是代码实现了,别看讲了这一堆,其实代码很好写
int Add(int x, int y)//传入需要需要相加的数
{
while (y)//y就是进位信息,为0时跳出循环
{
int a = x ^ y;//利用临时变量保证下一步计算进位信息x不变
y = (x & y) << 1;//进位信息
x = a;//把去掉进位信息的结果赋给a,重复上述操作
}
return x;
}
代码就这么短,骚不骚?哈哈哈,这篇博客写的爽,铁子们后面的内容更骚,嘿嘿嘿!!!
🚀减法的实现
减法就没什么技术含量了,因为比如5-4还可以写成5+(-4),套上前面写的加法然后,给减数改成相反数即可
相反数怎么整?让阿辉装一手,嘿嘿
原反补码,阿辉就不讲了,默认大家都会
按位取反操作符~,一个数取反后,符号位会改变,这么一整,该数的正负相反了,符号位以外的数也取反了,如果再加个1,大家不看符号位这不就是负数原码得到补码的过程,哟,这不拿捏了-a = ~a + 1
代码不就好写了:
int Sub(int x, int y)//传入被减数与减数
{
return Add(x, ~y + 1);//减数取相反数后与被减数相加
}
🚀乘法的实现
乘法也是稀松平常,没什么难理解的地方,怎么实现呢?铁子们别急,阿辉整个例子你们就懂了👊
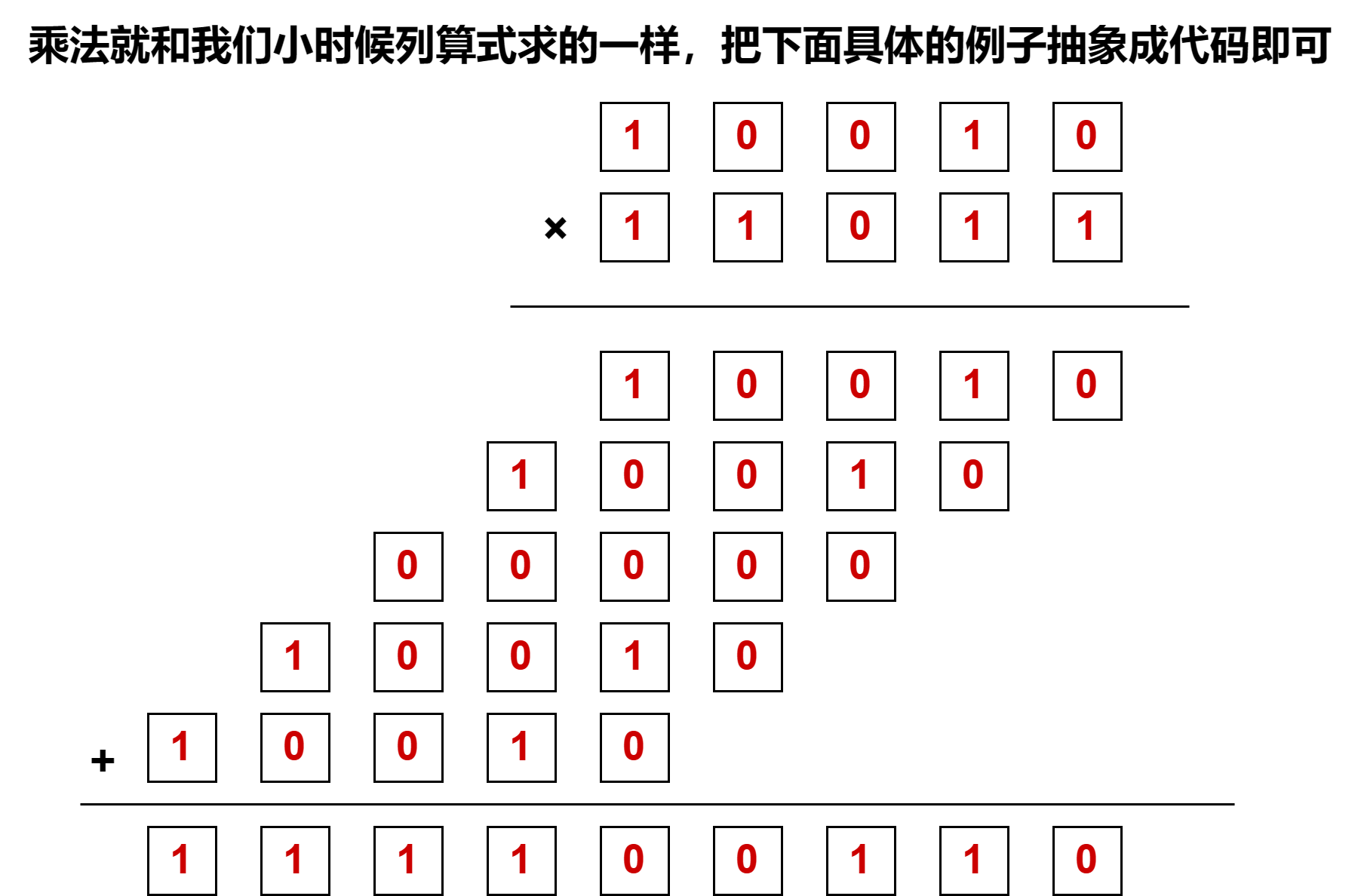
铁子们这里阿辉,先给出代码再解释:
int Mul(int x, int y)//传进来两数
{
int ret = 0;//作返回值
for (int i = 0; i <= 30; i = Add(i, 1))//符号位不算,固定循环31次
{
//遍历y的除符号位的31位,判断是否为1
if (y >> i & 1 == 1)//对应二进制位为1,进入if
{
//因为二进制位只有0和1,0乘任何数还是0,所以不用管
//当为1时,1乘任何数还是它本身,所以加上x
ret = Add(ret, x);
}
//遍历一次x左移一位,因为再循环,y向后一位找1
//这个1代表2的i次方,相当于把这个2的i次方乘在了x上
//左移一位相当于乘2,右移一位相当于除2
x <<= 1;
}
return ret;
}
铁子们注意,上述实现的乘法可以计算负数,为什么呢?这与原反补码有关,阿辉水平有限解释不出来,铁子们感兴趣可以研究一下,找到记得和阿辉分享一波,嘿嘿
铁子们,没懂的话可以自己想想试试,如果实在不懂可以私信我好吧,下面的除法才是重头戏特别麻烦 💀
🚀除法的实现
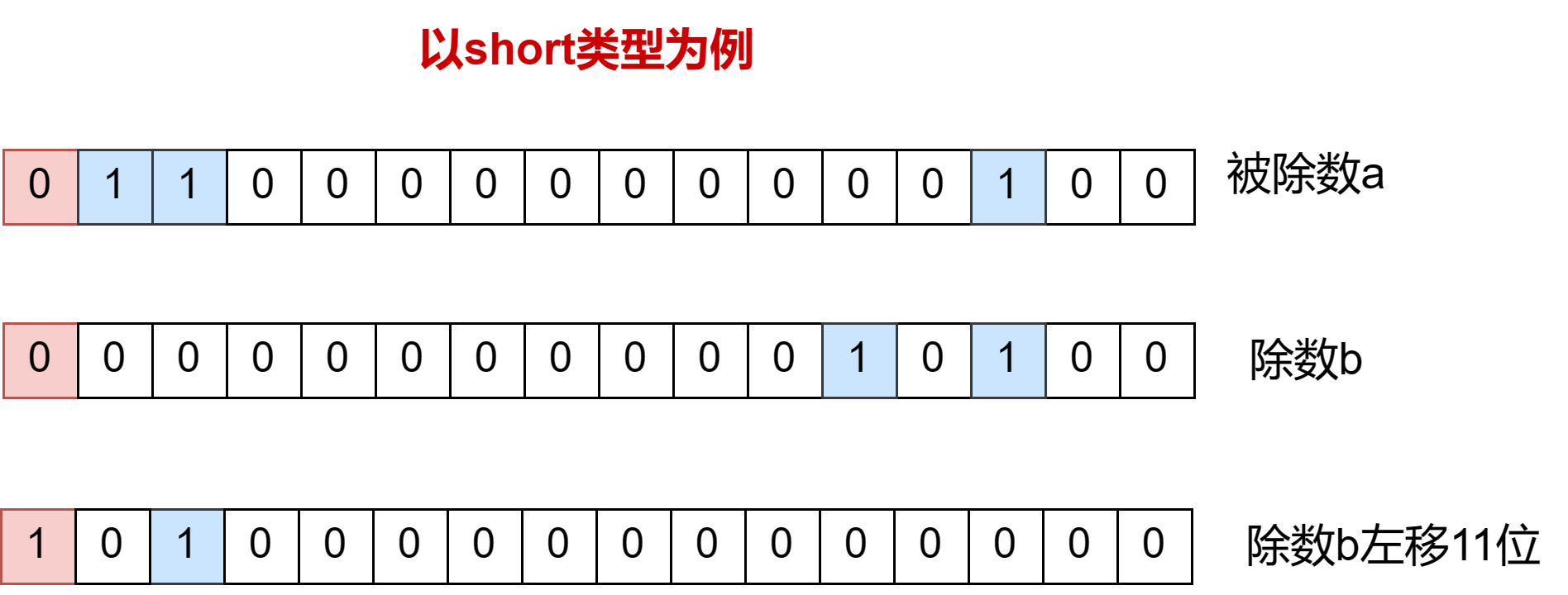
除法比较麻烦,这里阿辉实现的除法是整数除法,上图给大家引导:
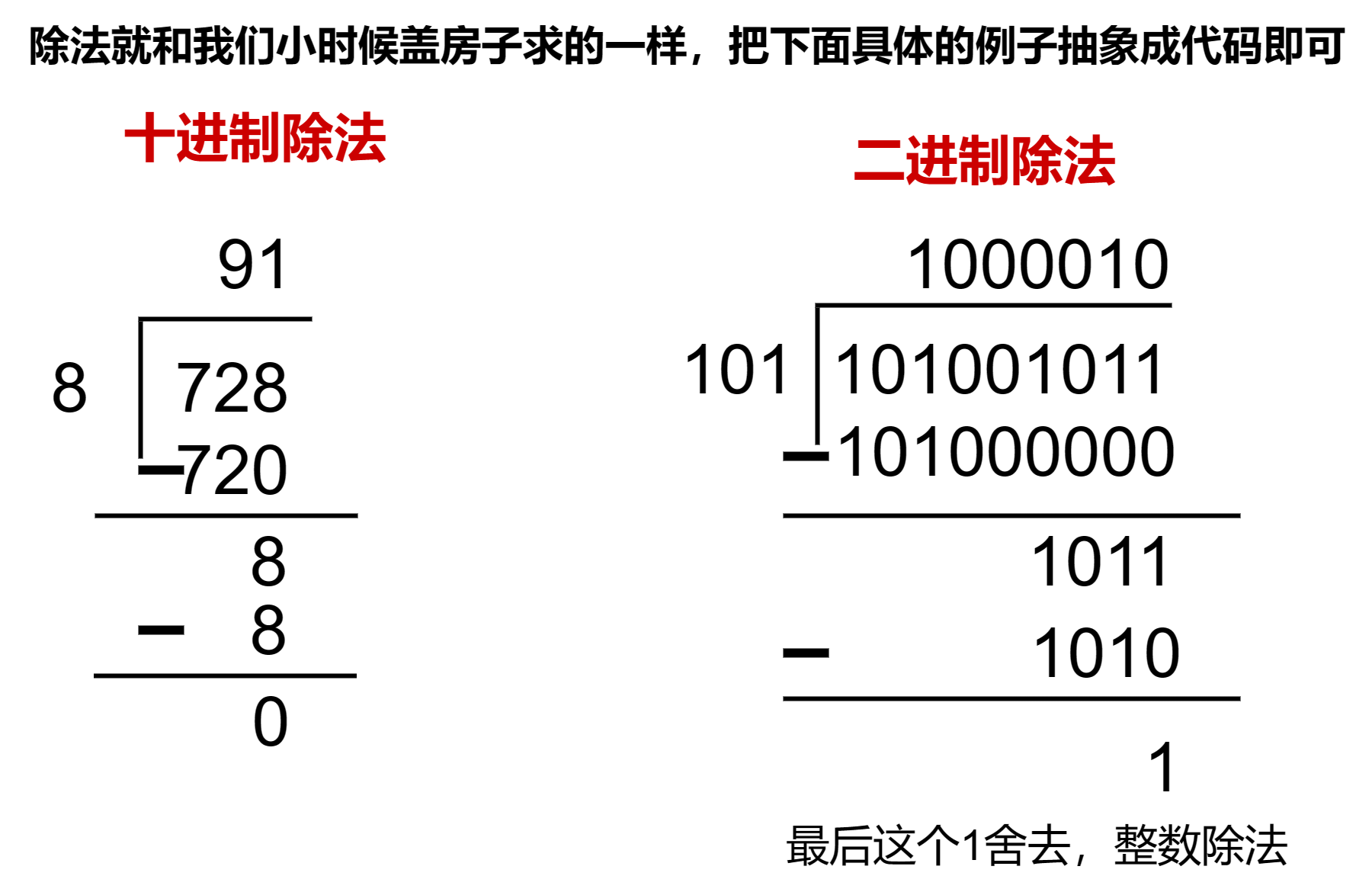
关于将除法抽象成代码,这是一个相当复杂的过程。首先,让我们回顾一下如何进行除法运算。在我们最常见的十进制系统中,以被除数728÷8为例,我们是如何得出十位上的9的呢?除法运算实际上是在找到一个最大的数,使得将除数8乘以这个数接近被除数728,然后再用728减去这个数720(8×90),然后继续这个过程,要么除尽要么除不尽。不过在整数除法中,如果除不尽就舍去余数。实际上,二进制数的除法运算也是类似的过程。与十进制不同的是,二进制位只有1,因此只需要将除数101后面加上0来逼近被除数101001011(在二进制中,将除数101左移一位就相当于除数后面加上一个0),然后用101001011减去101×1000000(101左移6位),然后重复这个操作直到除尽
但是我们在写代码时不能通过除数左移去逼近,因为这样会有风险
红色方块的位置代表符号位。我们给除数b左移,左移一位比a小,继续左移直到比a大才知道上一次左移逼近被除数a。但是对于我们给的这个例子b怎么左移也不可能比a大,因为当b右移11位时,符号位变成1了,b直接变成负数了。
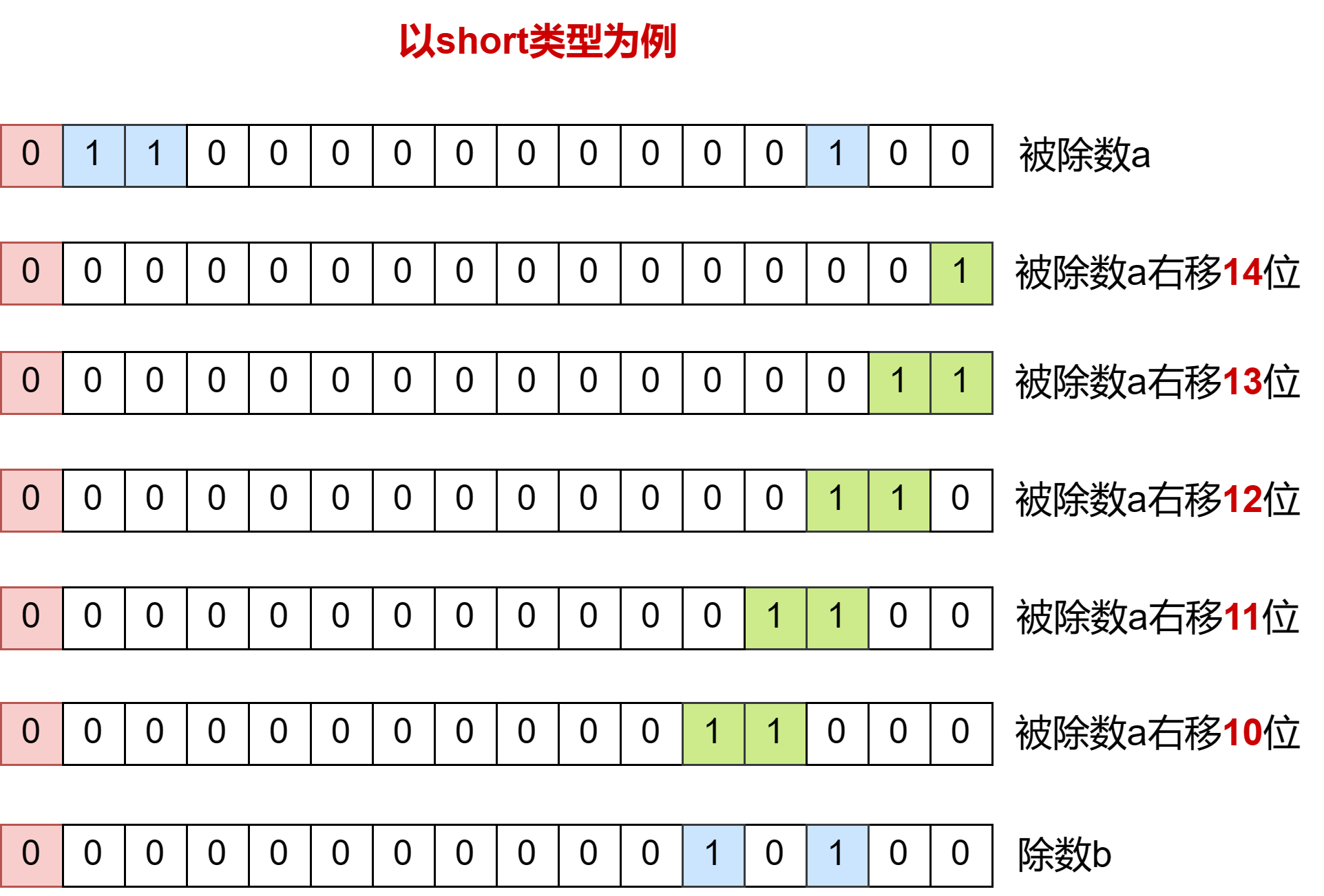
这里我们通过被除数右移代替除数左移来逼近除数达到一样的效果,因为被除数右移多少位逼近除数也就是除数左移多少位逼近被除数,这样就不会有改变符号位的风险
我们让除数a从右移14位开始,然后右移位数依次递减,当a右移10位时第一次大于b也就是b左移10位逼近a,然后a减去b左移10位后的数得到的结果重复上述操作第一次找到的就是最高位的1就像我们算十进制除法一样,我们首先找到千位随后就是百位、十位只不过二进制只有0和1很多位都是0
铁子们,下面我会根据代码讲,尽我所能讲明白好吧!
首先,我们实现的除法并不能处理负数,要先把负数处理成正数
这里我们实现一个函数oppo()求相反数
int oppo(int x)//相反数
{
return Add(~x, 1);//上面减法的时候解释过了
}
下面是关于除法的具体实现(不包括系统最小值)
int dived(int x, int y)//不含系统最小数的除法
{
//负数改正数,正数则不变
int a = x < 0 ? oppo(x) : x;//小于0就取相反数
int b = y < 0 ? oppo(y) : y;
int ret = 0;//作返回值
//除了符号位,遍历31次
for (int i = 30; i >= 0; i = Sub(i, 1))
{
//i从30开始依次递减
//当a第一次右移i位大于b时,说明最高位的数字找到了
//进入if把值加到返回值ret上
if (a >> i >= b)
{
ret |= 1 << i;//ret初始值时0,把1或上去
a = Sub(a, Mul(b,ret));//同时更新a的值,a=a-b×ret
}
}
//只有x和y不同时为负数或正数时要取相反数
//x,y同时大于或小于0,相除就是正数嘛
//异或值相等为0嘛就是假
//这个异或骚不骚,代替了下面这么挫的代码
//if((x > 0 && y < 0) || (x < 0 && y > 0))
if (x > 0 ^ y > 0)
return oppo(ret);//取相反数
return ret;
}
包含系统最小值,int类型的取值为-2^30^ ~ 0 ~ 2^30^-1,因为0是包含在正数里的,所以系统最小值的绝对值大于系统最大值,所以我们面临一个问题,系统最小值没有它的相反数,所以求系统最小值我们要单独拎出来求
五种情况(x是被除数,y是除数):
- x,y都是系统最小,直接返回
1 - y是系统最小,x不是,直接返回
0(整数除法) - x是系统最小,y是-1,那结果就是系统最小的绝对值,值域没这个数,直接返回-1
- x,y都不是系统最小,咱们上面实现的那个代码就是
- x是系统最小,y不是,这个情况就是我们下面要解决的
x是系统最小,y不是,这里我们无法给它取相反数,我们给x拆成两部分,
a=(x+1)得到的就不是系统最小了,用b = (a÷y),可以用我们上面的dived()这个函数来求,然后在用c = x - (b × y),接着a = c ÷ y,最后a+b就是x÷y的结果
就是上面这张图这个原理,没啥难的,不一定要加1,2、3、4……都可以
INT_MIN被宏定义成int类型的最小值,使用需要引<limits.h>头文件
int Div(int x, int y)
{
if (x == INT_MIN && y == INT_MIN)
return 1;
else if (x == INT_MIN && y == -1)
return -1;
else if (y == INT_MIN)
return 0;
//这就是上面解释的代码
else if (x == INT_MIN)
{
int a = Add(x, 1);
int b = dived(a, y);
a = dived(Sub(x, Mul(b, y)), y);
return Add(a, b);
}
else
return dived(x,y);//不含系统最小值的除法
}
coding有三点要注意:
- 负数要先转化成正数
- 被除数左移会有风险
- 系统最小无法取相反数
加减乘除的完整代码,他们并不是孤立的,互相调用
#include<stdio.h>
#include<limits.h>
int Add(int x, int y)
{
while (y)
{
int a = x ^ y;
y = (x & y) << 1;
x = a;
}
return x;
}
int Sub(int x, int y)
{
return Add(x, Add(~y, 1));
}
int Mul(int x, int y)
{
int ret = 0;
for (int i = 0; i <= 30; i = Add(i, 1))
{
if (y >> i & 1 == 1)
{
ret = Add(ret, x);
}
x <<= 1;
}
return ret;
}
int oppo(int x)
{
return Add(~x, 1);
}
int dived(int x, int y)
{
int a = x < 0 ? oppo(x) : x;
int b = y < 0 ? oppo(y) : y;
int ret = 0;
for (int i = 30; i >= 0; i = Sub(i, 1))
{
if (a >> i >= b)
{
ret |= 1 << i;
a = Sub(a, Mul(b,ret));
}
}
if (x > 0 ^ y > 0)
return oppo(ret);
return ret;
}
int Div(int x, int y)
{
if (x == INT_MIN && y == INT_MIN)
return 1;
else if (x == INT_MIN && y == -1)
return -1;
else if (y == INT_MIN)
return 0;
else if (x == INT_MIN)
{
int a = Add(x, 1);
int b = dived(a, y);
a = dived(Sub(x, Mul(b, y)), y);
if (x > 0 ^ y > 0)
return oppo(Add(a, b));
return Add(a, b);
}
else
return dived(x,y);
}
好的,到这里阿辉就讲完了,说实话不容易,着力于构思怎么把铁子们讲懂,应该没有比我更细节的了,写完这篇满满成就感,铁子们觉得讲得不错的话给阿辉评论区扣个666,哈哈哈!!!!