一、快速排序有三种方法:hoare版本、挖坑法、前后指针版本
但是三种方法的核心思想都是一样的,都是将该数组分为左右两半递归式的排序。
1.hoare版本

该方法是先保存a[keyi]位置的值,然后右边先开动找小,找到小后,左边开动找大,找到大之后,两数互换,最后,相遇位置与a[keyi]位置互换(即默认每次相遇位置都是小于a[keyi]):
int PartSort1(int* a, int begin, int end)
{
int midi = GetMidi(a, begin, end);
Swap(&a[midi], &a[begin]);
int left = begin, right = end;
int keyi = begin;
while (left < right)
{
// 右边找小
while (left < right && a[right] >= a[keyi])
{
--right;
}
// 左边找大
while (left < right && a[left] <= a[keyi])
{
++left;
}
Swap(&a[left], &a[right]);
}
Swap(&a[left], &a[keyi]);
return left;
}那为什么默认相遇位置比a[keyi]小呢?

2.挖坑法
该方法是先把第一个数据存放在临时变量key中,形成一个坑位,然后r向左走(r--),直到找到比key小的,将r的值放入l中,r处形成一个坑位,然后l向右走(l++),直到找到比key大的……以此循环。
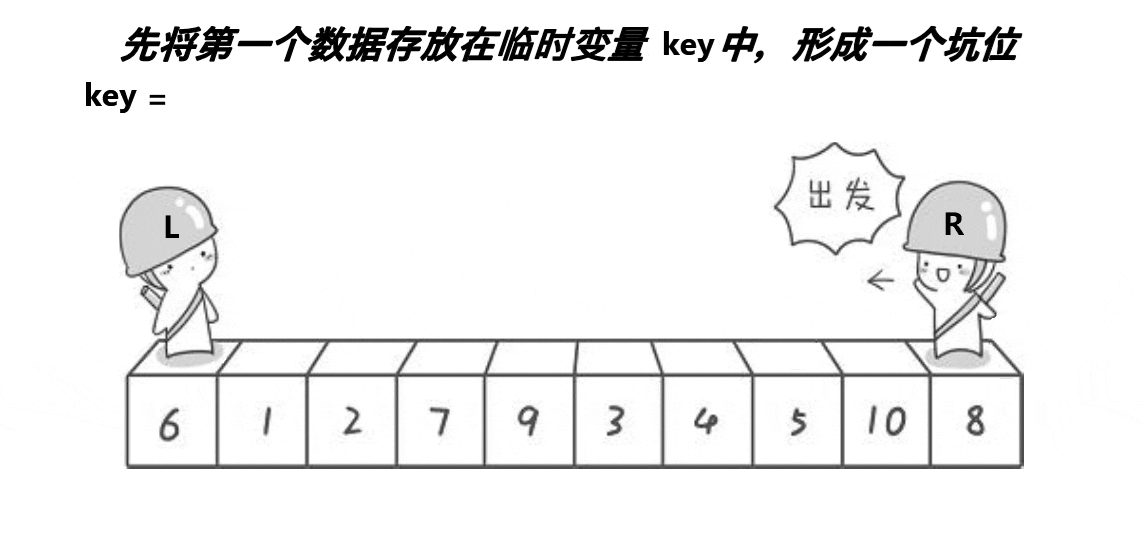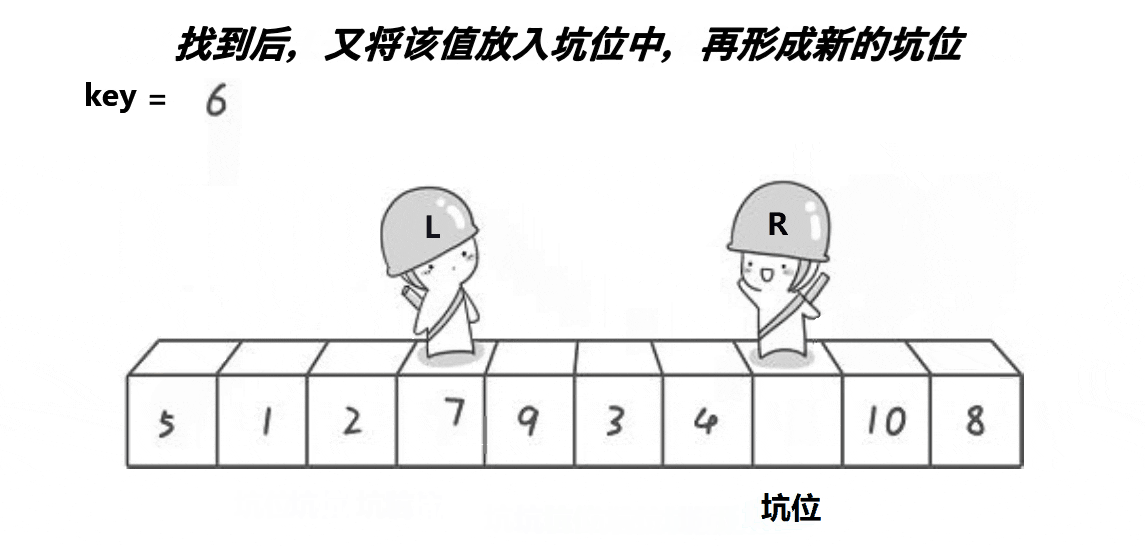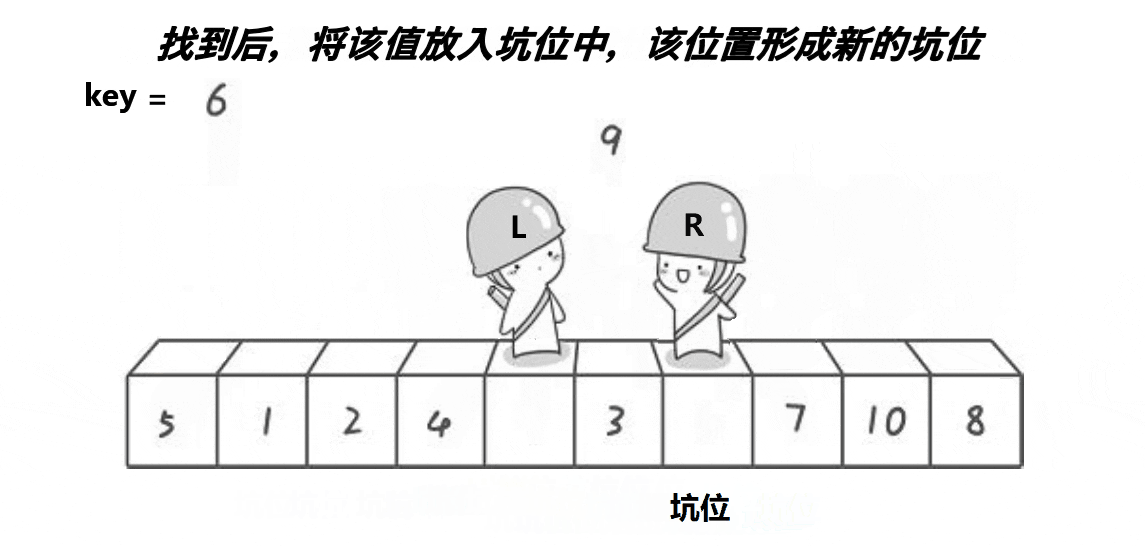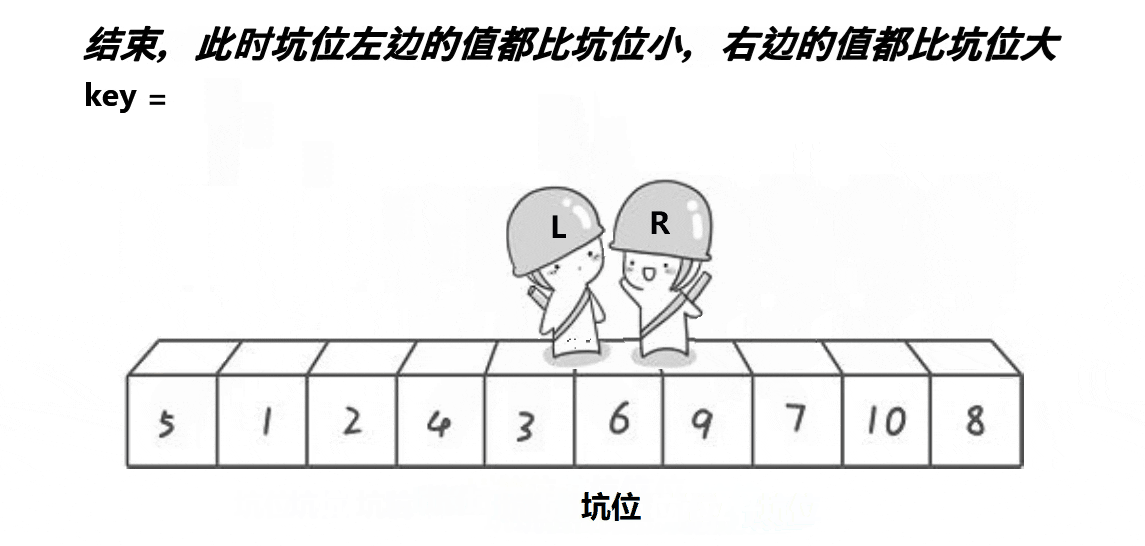
int PartSort2(int* a, int begin, int end)
{
int midi = GetMidi(a, begin, end);
Swap(&a[midi], &a[begin]);
int key = a[begin];
int hole = begin;
while (begin < end)
{
// 右边找小,填到左边的坑
while (begin < end && a[end] >= key)
{
--end;
}
a[hole] = a[end];
hole = end;
// 左边找大,填到右边的坑
while (begin < end && a[begin] <= key)
{
++begin;
}
a[hole] = a[begin];
hole = begin;
}
a[hole] = key;
return hole;
}
3.前后指针版本
该方法是将第一个数据保存至临时变量key中,利用两个指针,prev = begin,cur = prev + 1,cur向前进(cur++),遇到比key小时,让a[pre
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
return;
int keyi = PartSortn(a, begin, end);
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
v+1]与a[cur]位置的数据进行交换,以此往复循环。

快排:
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
return;
int keyi = PartSortn(a, begin, end);
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
找三数中值:
int GetMidi(int* a, int begin, int end)
{
int midi = (begin + end) / 2;
// begin midi end 三个数选中位数
if (a[begin] < a[midi])
{
if (a[midi] < a[end])
return midi;
else if (a[begin] > a[end])
return begin;
else
return end;
}
else // a[begin] > a[midi]
{
if (a[midi] > a[end])
return midi;
else if (a[begin] < a[end])
return begin;
else
return end;
}
}二、快排的非递归
为了实现快排的非递归,我们就需要借助基本数据结果栈来解决:
每次都可以插入头和尾(begin、end)的数据进入(STPush),由于后进先出原则,因此我们先插入end,再插入begin,取STTop赋值于left,Pop数据,再取STTop赋值于right,Pop数据,随后进行快排,这里其实就是一种递归思想的非递归。
代码:
void QuickSortNonR(int* a, int begin, int end)
{
ST s;
STInit(&s);
STPush(&s, end);
STPush(&s, begin);
while (!STEmpty(&s))
{
int left = STTop(&s);
STPop(&s);
int right = STTop(&s);
STPop(&s);
int keyi = PartSort3(a, left, right);
// [left, keyi-1] keyi [keyi+1, right]
if (left < keyi - 1)
{
STPush(&s, keyi - 1);
STPush(&s, left);
}
if (keyi + 1 < right)
{
STPush(&s, right);
STPush(&s, keyi + 1);
}
}
STDestroy(&s);
}C语言中栈的实现:
//Stack.h
#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>
typedef int STDataType;
typedef struct Stack
{
STDataType* a;
int top; // 标识栈顶位置的
int capacity;
}ST;
void STInit(ST* pst);
void STDestroy(ST* pst);
// 栈顶插入删除
void STPush(ST* pst, STDataType x);
void STPop(ST* pst);
STDataType STTop(ST* pst);
bool STEmpty(ST* pst);
int STSize(ST* pst);
//Stack.c
#include"Stack.h"
void STInit(ST* pst)
{
assert(pst);
pst->a = NULL;
pst->capacity = 0;
// 表示top指向栈顶元素的下一个位置
pst->top = 0;
// 表示top指向栈顶元素
//pst->top = -1;
}
void STDestroy(ST* pst)
{
assert(pst);
free(pst->a);
pst->a = NULL;
pst->top = pst->capacity = 0;
}
// 栈顶插入
void STPush(ST* pst, STDataType x)
{
assert(pst);
if (pst->top == pst->capacity)
{
int newcapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;
STDataType* tmp = (STDataType*)realloc(pst->a, sizeof(STDataType) * newcapacity);
if (tmp == NULL)
{
perror("realloc fail");
return;
}
pst->a = tmp;
pst->capacity = newcapacity;
}
pst->a[pst->top] = x;
pst->top++;
}
//栈顶删除
void STPop(ST* pst)
{
assert(pst);
// 不为空
assert(pst->top > 0);
pst->top--;
}
STDataType STTop(ST* pst)
{
assert(pst);
// 不为空
assert(pst->top > 0);
return pst->a[pst->top - 1];
}
bool STEmpty(ST* pst)
{
assert(pst);
/*if (pst->top == 0)
{
return true;
}
else
{
return false;
}*/
return pst->top == 0;
}
int STSize(ST* pst)
{
assert(pst);
return pst->top;
}