题目

操作给定的二叉树，将其变换为源二叉树的镜像。

数据范围：二叉树的节点数 0≤n≤1000， 二叉树每个节点的值 0≤val≤1000。

要求： 空间复杂度 O(n)。本题也有原地操作，即空间复杂度 O(1)的解法，时间复杂度 O(n)。

比如：

源二叉树

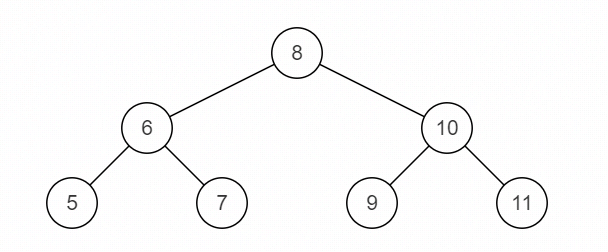
镜像二叉树

示例1

输入：{8,6,10,5,7,9,11}

返回值：{8,10,6,11,9,7,5}

示例2

输入：{}

返回值：{}

---

思路1：递归

先递归处理二叉树的左子树，再递归处理二叉树的右子树，然后将原二叉树根节点的左子树连接处理后的右子树，将原二叉树根节点的右子树连接处理后的左子树，即可完成二叉树的镜像。

---

代码1

import java.util.*;

/*
 * public class TreeNode {
 *   int val = 0;
 *   TreeNode left = null;
 *   TreeNode right = null;
 *   public TreeNode(int val) {
 *     this.val = val;
 *   }
 * }
 */

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param pRoot TreeNode类 
     * @return TreeNode类
     */
    public TreeNode Mirror (TreeNode pRoot) {
        // write code here
        if(pRoot == null || (pRoot.left == null && pRoot.right == null)) {
            return pRoot;
        }

        TreeNode left = Mirror(pRoot.left);
        TreeNode right = Mirror(pRoot.right);

        pRoot.left = right;
        pRoot.right = left;

        return pRoot;
    }
}

---

思路2：栈

二叉树中能够用递归的，大多也可以用栈来实现。栈的访问是一种自顶向下的访问，因此需要在左右子节点入栈后直接交换，然后再访问后续栈中内容。

具体做法：

• step 1：优先检查空树的情况。
• step 2：使用栈辅助遍历二叉树，根节点先进栈。
• step 3：遍历过程中每次弹出栈中一个元素，然后该节点左右节点分别入栈。
• step 4：同时我们交换入栈两个子节点的值，因为子节点已经入栈了再交换，就不怕后续没有交换。

---

代码2

import java.util.*;

public class Solution {
    public TreeNode Mirror (TreeNode pRoot) {
        //空树
        if(pRoot == null) {
            return null;
        }

        //辅助栈
        Stack<TreeNode> s = new Stack<>();
        //根节点先进栈
        s.push(pRoot);

        while(!s.isEmpty()) {
            TreeNode node = s.pop();
            //左右节点入栈
            if(node.left != null) {
                s.push(node.left);
            }
            if(node.right != null) {
                s.push(node.right);
            }

            //交换左右
            TreeNode temp = node.left;
            node.left = node.right;
            node.right = temp;
        }
        return pRoot;
    }
}