算法简介

数位统计 DP 用于数字的数位统计,是一种比较简单的 DP 套路题。

一个数字的数位有个位、十位、百位,等等,如果题目和数位统计有关,那么可以用 DP思想,把低位的统计结果记录下来,在高位计算时直接使用低位的结果,从而提高效率。用下面一道例题详解数位统计 DP 的建模和两种实现:递推和记忆化搜索。

数位统计有关的题目，基本内容是处理“前导 0”和“数位限制”

算法讲解

数字计数

问题描述:

给定两个正整数a 和b,求在[a,b]的所有整数中，每个数码digit)各出现了多少次

输入:输入两个整数a 和b。

输出:输出 10个整数,分别表示 0~9在[a,b]中出现了多少次。

数据范围:1ab<10的12次方

首先转换一下题目的要求。

区间[a,b]等于[1,a-1]与[1,b]的差分,把问题转换为在区间[1,x]内,统计数字 0~9 各出现了多少次。
由于 a 和b的值太大,用暴力法直接统计[a,b]内的每个整数显然会超时,需要设计一个复杂度约为 O(log2n)的算法。如何加快统计? 容易想到 DP-把对低位数的统计结果用于高位数的统计。例如,统计出三位数之后,继续统计一个四位数时,对这个四位数的后3位的统计直接引用前面的结果。以统计[0,324]内数位 2 出现了多少次为例,搜索过程如下图所示：其中，下划线的数字区间是前面已经计算过的，记录在状态dp【】中，不用再重算；符号*表示区间中有数位2，需要特殊处理。

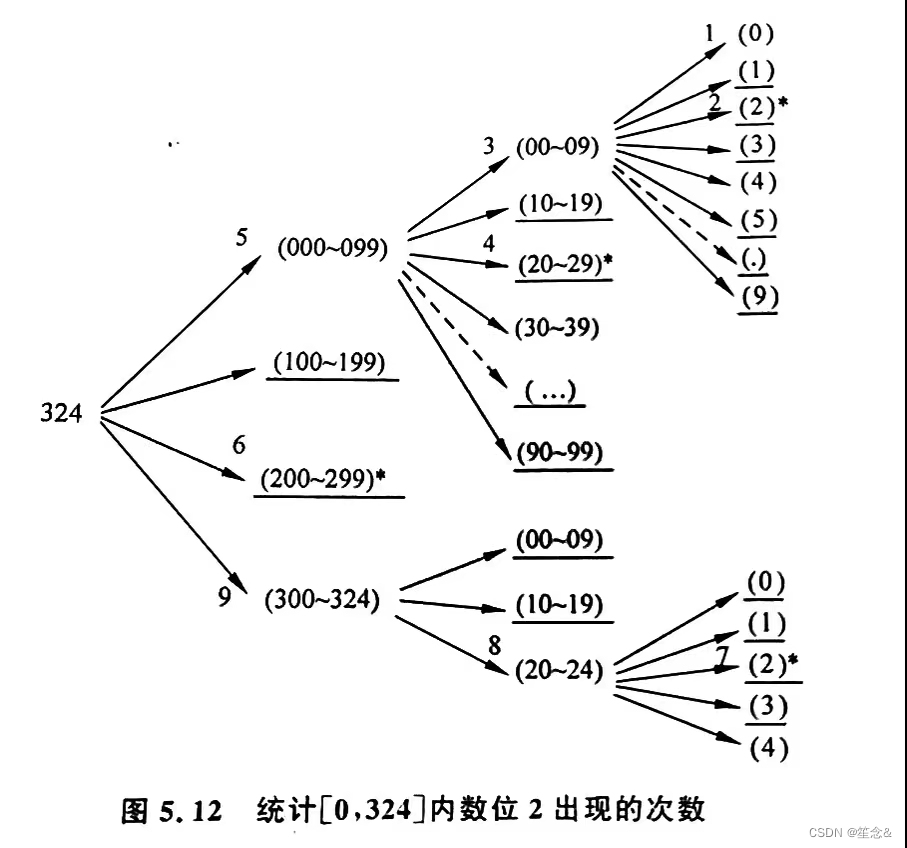
把[0,324]区间分解为4个区间:000~099、100-199、200~299、300~324。其中.000~099，100~199、200~299 能够沿用00~99 的计算结果。至于 300~324,最高位3不是要的数位2,等价于计算 00~24。
称数字前面的0为“前导 0”,如 000~099 中的 0。称每位的数字为“数位限制”,如 324中最高位的 3次高位的2、最低位的 4。计数统计时需要特判前导 0和数位限制，后面有细解释。
下面分别用递推和记忆化搜索两种编码方法实现

数位统计DP的递推实现

定义状态 dp[],dp[i]为i 位数的每种数字有多少个,说明如下。
(1)一位数 0~9,每种数字有 dp[1]=1个。
(2)二位数 00~99,每种数字有 dp[2]=20个。注意,这里是 00~99,不是0~99。如果是0~99,0 只出现了 11次。这里把0和其他数字一样看待,但编程时需要特殊处理,因为按照习惯写法,数字前面的0应该去掉,如 043 应该写成43。前导0在0~9,00~99,000~999
等所有情况下都需要特殊处理。
(3)三位数 000~999,每种数字有 dp[3]=300 个。
(4)四位数 0000~9999,每种数字有 dp[4]=4000个,依此类推

dp[i]有两种计算方法。

(1)dp[i]=dp[i-1]X10+10的i-1次方,这是从递推的角度分析得到的。以数字 2为例,计算dp[2]时,2在个位上出现了dp[i-1]X10=dp[1]X10=10 次,即2,12,22.....;92;在十位上出现了 10的i-1次方=10的2-1 =10 次,即 20,21,22,...,29。计算 dp[3]时,2在个位和十位上出记了 dp[2]X10=200 次,在百位上出现了 10的3-1=100 次。

(2)dp[i]=iX10的i次方/10,这是按排列组合的思路得到的。因为从i个0递增到i个9,所有的字符共出现了iX10的i次方次,0~9 每个数字出现了iX10的i次方/10 次。

下面考虑如何编程。以[0,324]为例,先从324 的最高位开始,每种数字的出现次数 cnt.计算如下。
1)普通情况。例如,00~99 共出现了 3次,分别出现在 000~099、100~199、200一99 的后两位上,每个数字在后两位上共出现 dp[i-1]Xnum[i]=dp[2]X3=60 次。对应代码第 23 行。

(2) 特判当前的最高位,即“数位限制”。第 3 位上的数字有 0,1,2,3, 3 是最高位的数位限制。数字0,1、2 分别在 000~099、100~199、200~299 的最高位上出现了 100 次,对应码第 24 行;数字3在 300~324 中出现了 25 次,对应代码第 25~27 行。

(3) 特判前导 0。在前面的计算中,都把 0 和其他数字一样看待,但前导 0 应该去掉对应代码第 28 行。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=15;
ll ten[N],dp[N];
ll cnta[N],cntb[N];             //cnt[i]，统计数字“i”出现了多少次
int num[N];
void init(){                    //预计算dp[]
    ten[0] = 1;                 //ten[i]: 10的i次方
    for(int i=1;i<=N;i++){
        dp[i]  = i*ten[i-1];    //或者写成：dp[i]  = dp[i-1]*10+ten[i-1];
        ten[i] = 10*ten[i-1];
    }
}
void solve(ll x, ll *cnt){
    int len = 0;  //数字x有多少位
    while(x){     //分解x，num[i]是x的第i位数字
        num[++len] = x%10;
        x=x/10;
    }
    for(int i=len;i>=1;i--){                            //从高到低处理x的每一位
        for(int j=0;j<=9;j++)      cnt[j] += dp[i-1]*num[i];
        for(int j=0;j<num[i];j++)  cnt[j] += ten[i-1];  //特判最高位比num[i]小的数字
        ll num2 = 0;
        for(int j=i-1;j>=1;j--)    num2 = num2*10+num[j];
        cnt[num[i]] += num2+1;                          //特判最高位的数字num[i]
        cnt[0] -= ten[i-1];                             //特判前导0
    }
}
int main(){
    init();
    ll a,b;  cin >> a>>b;
    solve(a-1, cnta), solve(b, cntb);
    for(int i=0;i<=9;i++)  cout << cntb[i]-cnta[i] <<" ";
}

代码复杂度：solve（）函数有两层for循环，只循环了10*len次

数位统计DP的记忆化搜索实现

回顾记忆化搜索,其思路是在递归函数 dsO中搜索所有可能的情况，遇到已经计算过的记录在 dp 中的结果,就直接使用,不再重复计算。

用递归西数 dfs()实现上述记忆化搜索,执行过程如下。如图 5.12 所示,以[0,324]为例,从输入 324 开始,一直递归到最深处的(0),然后逐步回退,图中用箭头上的数字标识了回退的顺序。

记忆化搜索极大地减少了搜索次数。例如,统计 000~099 中 2 的个数,因为用 dp[]进行记忆化搜索,计算 5 次即可;如果去记忆化部分,需要检查每个数字,共 100 次。

下面设计 dp 状态。和前面递推的编码类似,记忆化搜索的代码中也需要处理前导 0和每位的最高位。编码时,每次统计 0~9 中的一个数字,代码中用变量 now 表示这个数字下面的解释都以 now=2 为例。

定义状态 dp[][],用来记录 0~9,00~99,000~999 这样的无数位限制情况下 2 的个数,以及 20~29、200~299、220~229、2200~2299 这种前面带有 2 的情况下2 的个数。

dp[pos][sum]表示最后 pos 位范围是[0---0,99.--9],前面 2 的个数为 sum 时,数字2的总个数。例如,dp[1][0]=1 表示 00~09,10~19,30~39,..区间内 2 的个数为 1；dp[1][1]=11 表示 20~29 区间内 2 的个数为11; dp[1][2]=21 表示 220~229 区间内的个数为 21; dp[1][3]=31 表示 2220~2229 区间内 2 的个数为 31;dp[2][0]=20 表示000~099,100~199,300~399,400~499,-..区间内 2 的个数为 20; dp[2][1]=120 表200~299 区间内 2的个数为 120; dp[2][2]=220 表示 2200~2299 区间内 2的个数为220;等等。

用lead 标识是否有前导 0,lead=false 表示没有前导 0,lead=true 表示有前导0。

用 limit 标识当前最高位的情况,即“数位限制”的情况。如果是 0~9,limit=false;否则 limit=true。例如[0,324],计算 324 的最高位时,范围是0~3,此时 limit=true。再如从最高位数字 1递归到下一位时,下一位的范围是 0~9,此时 limit=false。如果不太理解，请对比前面递推实现的解释。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 15;
ll dp[N][N];
int num[N],now;                 //now：当前统计0~9的哪一个数字
ll dfs(int pos,int sum,bool lead, bool limit){    //pos：当前处理到第pos位
    ll ans = 0;
    if(pos == 0) return sum;    //递归到0位数，结束，返回
    if(!lead && !limit && dp[pos][sum]!=-1)  return dp[pos][sum];  //记忆化搜索
    int up = (limit ? num[pos] : 9);    //这一位的最大值，例如324的第3位是up = 3
    for(int i=0;i<=up;i++){                                         //下面以now=2为例：
        if(i==0 && lead)  ans += dfs(pos -1, sum,  true, limit&&i==up); // 计算000~099
        else if(i == now) ans += dfs(pos -1, sum+1,false,limit&&i==up); // 计算200~299
        else if(i != now) ans += dfs(pos -1, sum,  false,limit&&i==up); // 计算100~199
    }
    if(!lead && !limit) dp[pos][sum] = ans;       //状态记录：无前导0
    return ans;
}
ll solve(ll x){
    int len = 0;       //数字x有多少位
while(x){ 
num[++len] = x%10; 
x/=10;
}
    memset(dp,-1,sizeof(dp));
    return dfs(len,0,true,true);
}
int main(){
    ll a,b;    cin>>a>>b;
    for(int i=0;i<10;i++)   now = i, cout << solve(b)-solve(a-1)<<" ";  
    return 0;
}

记忆化搜索代码的复杂度和递推一样；

算法实践

一 Windy数

问题描述:不含前导0且相邻两位数字之差至少为 2的正整数称为 Windy 数。问在a和b之间(包括a和b),总共有多少个 Windy数?(特例:把一位数0~9 看成 Windy数)

输入:输入两个整数 a 和b,I<= a <=b<= 2X10的9次方

输出:输出一个整数,表示答案。

输入样例:25 50

输出样例:20

题目分析：

在输入样例[25,50]区间中,32、33、34、43、44，45 不是 Windy 数,如数字 32,3-2=1<2

求区间[a,b]内的 Windy数,可以转换为分别求[1,a-1]和[1,b]区间。问题转换为定一个数z,求[o,z]内有多少个 Windy 数。
这是一道明显的数位统计 DP 题。检查一个很大的数时,对高位部分的检查可以沿用低位部分的检查结果。例如,计算0~342 的 Windy 数,分为统计 000~099、100~199、200~299，300~342 内的 Windy 数。这与前面的模板题的思路一样。
定义状态 dp[pos][last],表示数字长度为 pos 位,前一位是 last 的情况下(包括前导的无数位限制的 Windy 数总数。
例如,dp[1][0]=8 表示 00~09 区间内 Windy 数有 8个,数字长度 pos=1,前一位 last=1，注意此时前导0也是合法的,其中 00 和 01 不是 Windy 数,02~09 是 Windy 数,共8个。如果不算前导0,0~9内应该有 10个 Windy 数。
dp[1][1]=7 表示 10~19 区间内 Windy 数有 7个;dp[1][2]=7 表示 20~29 区间内Windy数有 7个;dp[2][0]=57 表示 000~099 区间内 Windy 数有 57 个,此时前导0也是合法的,如果不算前导 0,0~99 区间内应该有 74 个 Windy 数;dp[2][1]=50 表示 100~199 区间内 Windy数有 50 个; dp[2][2]=51 表示 200~299 区间内 Windy 数有51个；dp[2][3]=51表示 300~399 区间内 Windy 数有 51 个;dp[3】[1]=362 表示 1000~1999区间内 Windy数有 362个。
本题的代码与模板题相似。其中,lead 和 limit 变量的含义也相同,分别标识前导 0 和数位限制。

代码：

#include<bits/stdc++.h>
using namespace std;
int dp[15][15], num[15];
int dfs(int pos, int last, bool lead, bool limit){
    int ans = 0;
    if(pos == 0) return 1;
    if(!lead && !limit && dp[pos][last]!=-1) return dp[pos][last];
    int up = (limit?num[pos]:9);
    for(int i=0;i<=up;i++){
        if(abs(i-last)<2)  continue;   //不是windy数
        if(lead && i==0)   ans += dfs(pos-1,-2,true, limit&&i==up);
        else               ans += dfs(pos-1,i,false, limit&&i==up);
    }
    if(!limit && !lead)   dp[pos][last] = ans;
    return ans;
}
int solve(int x){
    int len = 0;
    while(x) { num[++len]=x%10; x/=10;}
    memset(dp,-1,sizeof(dp));
    return dfs(len,-2,true,true);   
}
int main(){
    int a,b; cin >>a>>b;
    cout << solve(b)-solve(a-1);
    return 0;
}

二手机号码

问题描述: 选手机号码,号码必须同时包含两个特征:手机号码中至少要出现3个相邻的相同数字;号码中不能同时出现 8和4。例如满足条件的号码有 13000988721、23333333333、14444101000;而不满足条件的号码有 1015400080、10010012022。手机号码一定是 11 位数，不含前导 0。给出两个数a 和b,统计出[a,b]区间内所有满足条件的号码数量。a 和b也是11 位的手机号码。
输入:两个整数a和b,10的10<= a <=b <=10的11
输出: 输出一个整数表示答案。

输入样例:
12121284000 12121285550

输出样例: 5

题目解析：

本体可以回避前导0.因为号码是11位的，最高位为1~9，只要限定最高位不为0即可

定义状态 dp[pos][u][v][state][n8][n4],其中 pos 表示当前数字长度,u 表示前一位数字,v 表示再前一位数字,state 标识是否出现 3 个连续相同数字,n8 标识是否出现8,标识是否出现 4。

代码：


#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll dp[15][11][11][2][2][2];
int num[15];
ll dfs(int pos,int u,int v,bool state,bool n8,bool n4,bool limit){
    ll ans=0;
	if(n8 && n4) return 0;    //8和4不能同时出现
	if(!pos) return state;
	if(!limit && dp[pos][u][v][state][n8][n4]!=-1) return dp[pos][u][v][state][n8][n4];
	int up = (limit?num[pos]:9);
	for(int i=0;i<=up;i++)
		ans += dfs(pos-1,i,u,state||(i==u&&i==v),n8||(i==8),n4||(i==4),limit&&(i==up));
	if(!limit)  dp[pos][u][v][state][n8][n4]=ans;
	return ans;
}
ll solve(ll x){
	int len = 0;
	while(x){num[++len]=x%10; x/=10;}
	if(len!=11) return 0;
	memset(&dp,-1,sizeof(dp));
	ll ans = 0;
	for(int i=1;i<=num[len];i++)        //最高位1~9，避开前导0问题
		ans+= dfs(len-1,i,0,0,i==8,i==4,i==num[len]);
	return ans;
}
int main(){
	ll a,b;  cin >> a>>b;
	cout <<solve(b)-solve(a-1);
}