昨天和之前打比赛的队友聊天,他说他面百度面到这道算法题,然后他用暴力法解的,面试官让他优化他没优化出来,这道题我之前没写过,我就想看看我能不能用效率高一点的方法把它做出来,我一开始就在想用递归或者翻转字符串等等技巧,想了半个多小时都想不到,然后算了,我也用暴力法吧,然后就写了如下代码:
class Solution {
public String longestPalindrome(String s) {
int n = s.length();
String ans = "";
for(int i = 0;i<n;i++){
int l = i, r=i;
while(l<= r && l >=0 && r < n && s.charAt(l) == s.charAt(r)){
String tem =s.substring(l,r+1);
if(r-l+1 > ans.length())ans=tem;
l--;r++;
}
l = i;r=l+1;
while(l >=0 && r < n && s.charAt(l) == s.charAt(r)){
String tem =s.substring(l,r+1);
if(r-l+1 > ans.length())ans=tem;
l--;r++;
}
}
return ans;
}
}这个暴力法就非常简单了,就是遍历字符的每个字符,然后以这个字符为中心用左右指针往两边移动,然后是写了两个while,一个是左右指针指向同一个字符然后向左右移动,还有一个是左右指针指向相邻的字符向两边移动。
还是看看官方题解的做法吧。
题解的方法一是用的动态规划:
class Solution {
public String longestPalindrome(String s) {
int len = s.length();
if(len < 2)return s;
boolean[][] dp = new boolean[len][len];
for(int i=0;i<len;i++){
dp[i][i] = true;
}
int begin =0;
int maxLen =1;
char[] str = s.toCharArray();
for(int L =2;L<=len;L++){
for(int i=0;i<len;i++){
int j = i+L-1;
if(j>=len){
break;
}else{
if(str[i] != str[j]){
dp[i][j] = false;
}else{
if(j-i<3){
dp[i][j] = true;
}else{
dp[i][j] = dp[i+1][j-1];
}
}
}
if(dp[i][j] && j-i+1 > maxLen){
maxLen = j-i+1;
begin = i;
}
}
}
return s.substring(begin, begin+maxLen);
}
}dp[i][j]表示s的第i个字符到第j个字符这一个子串是不是一个回文字符串。
首先,初始状态:dp[i][i] = true;
然后,状态转移方程:dp[i][j] = ?
第一种情况,s.charAt(i) != s.charAt(j), 那么dp[i][j] = false;
第二种情况,s.charAt(i) == s.charAt(j),如果子串长度小于3,那么dp[i][j]=true;否则dp[i][j] = dp[i-1][j+1]
只要找出dp[i][j]中为true且长度最大的那个就行,这一步在填充dp的数组的同时进行,不用另外遍历,只要一个max动态更新就行。然后值得注意的是这里是把字符串转成了字符数组,因为我们需要频繁的找字符串中的字符,用数组效率更高,用charAt方法需要遍历字符串,而数组可以直接通过寻址公式得出。
题解的第二种方法用的是中心扩展,和我的方法差不多,只是它把while循环封装成了函数而已,以下是题解方法二代码:
class Solution {
public String longestPalindrome(String s) {
if (s == null || s.length() < 1) {
return "";
}
int start = 0, end = 0;
for (int i = 0; i < s.length(); i++) {
int len1 = expandAroundCenter(s, i, i);
int len2 = expandAroundCenter(s, i, i + 1);
int len = Math.max(len1, len2);
if (len > end - start) {
start = i - (len - 1) / 2;
end = i + len / 2;
}
}
return s.substring(start, end + 1);
}
public int expandAroundCenter(String s, int left, int right) {
while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
--left;
++right;
}
return right - left - 1;
}
}
题解的方法三就比较高级了,时间复杂度只有O(n),叫Manacher算法:
定义一个概念”臂长“,如果一个回文字符串的长度是2*lenght+1,那么这个回文字符串的臂长就是length。
如果位置j的臂长为length那么如何找到位置i的臂长呢?
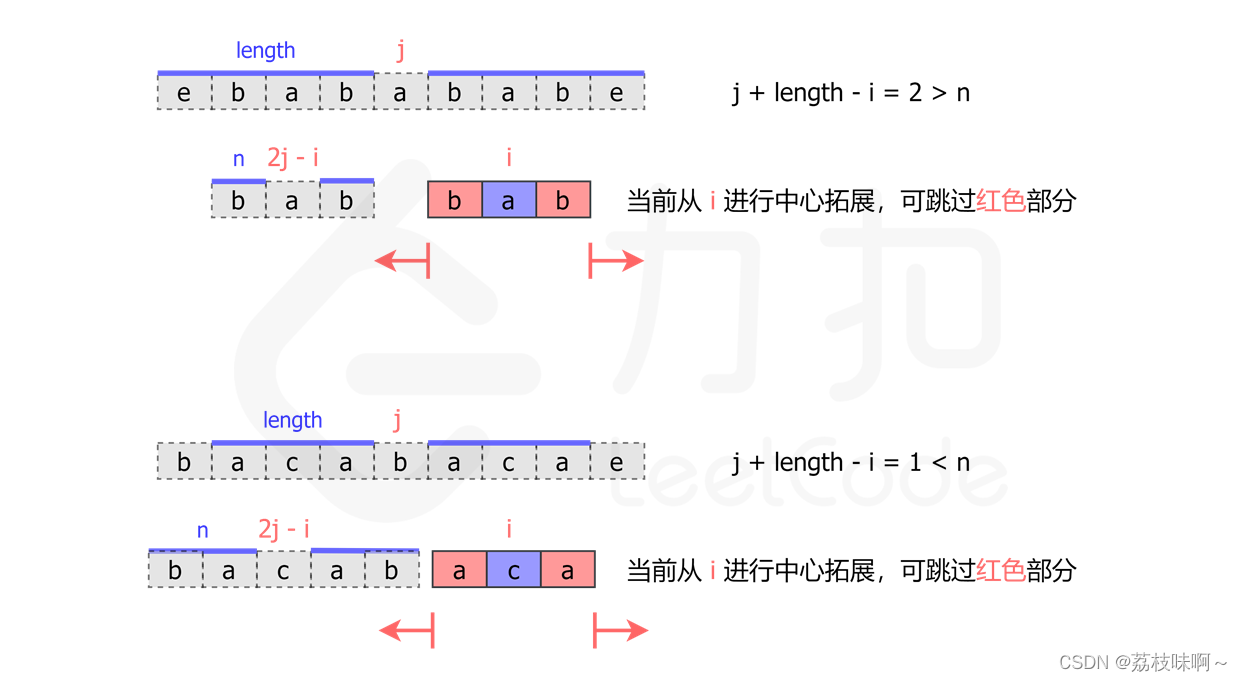
对于奇数长度的回文字符串而言:
如果i关于j的对称点2*j-i的臂长是n,那么位置i的臂长是min(n,2*j-i)。这个其实很好理解,因为j左右length拿一段是对称的,所以如果2*j-i有n的臂长按道理i也是这么大的臂长,但是只有length这一部分是对称的,而2*j-i的对称部分还可以向两边扩展,所以i的臂长只能取n和2*j-i的最小值。
偶数长度的回文字符串呢?
我们通过在字符串的两头和没两个字符之间加上#,这样无论奇数还是偶数长度的回文字符串都变成了奇数长度的回文字符串,比如aaba处理成#a#a#b#a#,偶数长度的回文字符串aa变成了#a#a#。aba还是变成奇数#a#b#a#。需要注意的是这里添加的#需要是字符串里面没有出现过的。最后记得把回文字符还原,把#去掉。以下是Manacher方法的代码:
class Solution {
public String longestPalindrome(String s) {
int start = 0, end = -1;
StringBuffer t = new StringBuffer("#");
for (int i = 0; i < s.length(); ++i) {
t.append(s.charAt(i));
t.append('#');
}
t.append('#');
s = t.toString();
List<Integer> arm_len = new ArrayList<Integer>();
int right = -1, j = -1;
for (int i = 0; i < s.length(); ++i) {
int cur_arm_len;
if (right >= i) {
int i_sym = j * 2 - i;
int min_arm_len = Math.min(arm_len.get(i_sym), right - i);
cur_arm_len = expand(s, i - min_arm_len, i + min_arm_len);
} else {
cur_arm_len = expand(s, i, i);
}
arm_len.add(cur_arm_len);
if (i + cur_arm_len > right) {
j = i;
right = i + cur_arm_len;
}
if (cur_arm_len * 2 + 1 > end - start) {
start = i - cur_arm_len;
end = i + cur_arm_len;
}
}
StringBuffer ans = new StringBuffer();
for (int i = start; i <= end; ++i) {
if (s.charAt(i) != '#') {
ans.append(s.charAt(i));
}
}
return ans.toString();
}
public int expand(String s, int left, int right) {
while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
--left;
++right;
}
return (right - left - 2) / 2;
}
}