一:基本概念
1.1 介绍
快速排序由C. A. R. Hoare在1962年提出,它是一种基于二叉树结构的交换排序算法,它采用了一种分治的策略,通常称其为分治法。该方法的基本思想是:先从数列中取出一个数作为基准数,然后将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边,再对左右区间重复第二步,直到各区间只有一个数。快速排序是一种不稳定的排序方法,但是他的效率非常快,比肩希尔和堆排序也略胜一筹。
快速排序(Quicksort)是对冒泡排序的一种改进。基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
1.2 排序流程
快速排序算法通过多次比较和交换来实现排序,其排序流程如下:
1、首先设定一个分界值,通过该分界值将数组分成左右两部分。
2、将大于或等于分界值的数据集中到数组右边,小于分界值的数据集中到数组的左边。此时,左边部分中各元素都小于或等于分界值,而右边部分中各元素都大于或等于分界值。
3、然后,左边和右边的数据可以独立排序。对于左侧的数组数据,又可以取一个分界值,将该部分数据分成左右两部分,同样在左边放置较小值,右边放置较大值。右侧的数组数据也可以做类似处理。
4、重复上述过程,可以看出,这是一个递归定义。通过递归将左侧部分排好序后,再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后,整个数组的排序也就完成了。
概括来说为 挖坑填数 + 分治法。
1.3 图解算法
快速排序主要有三个参数,left 为区间的开始地址,right 为区间的结束地址,Key 为当前的开始的值。
我们从待排序的记录序列中选取一个记录(通常第一个)作为基准元素(称为key)key=arr[left],然后设置两个变量,left指向数列的最左部,right 指向数据的最右部。
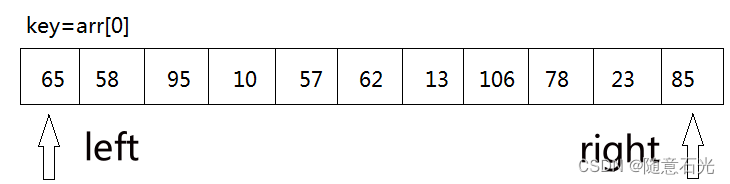
1.3.1 第一步
key 首先与 arr[right] 进行比较,如果 arr[right]<key,则arr[left]=arr[right]将这个比key小的数放到左边去,如果arr[right]>key则我们只需要将right–,right–之后,再拿arr[right]与key进行比较,直到arr[right]<key交换元素为止。
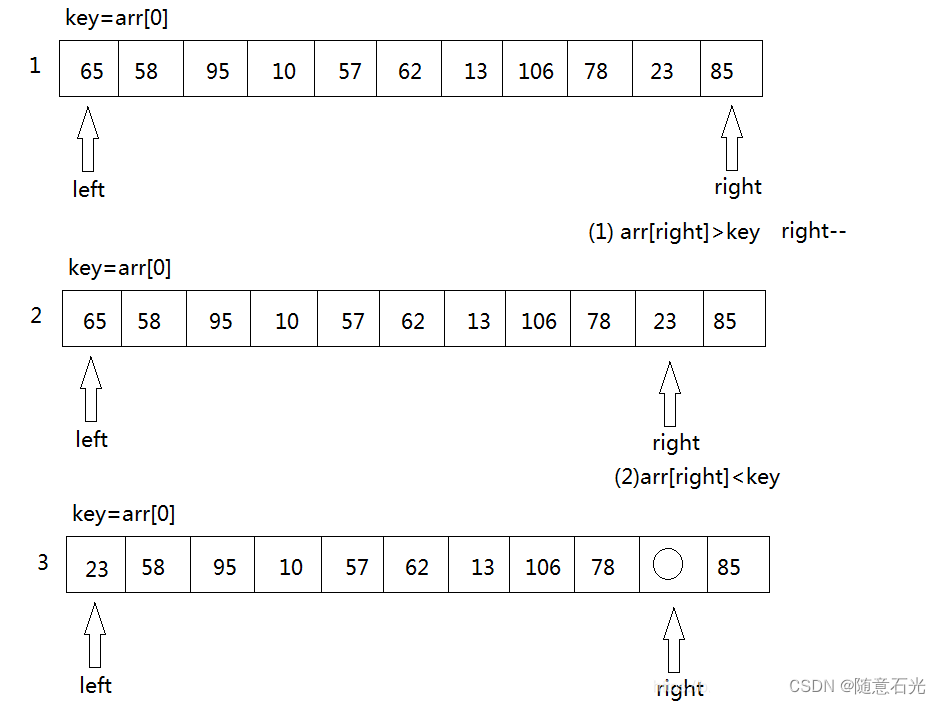
1.3.2 第二步
如果右边存在arr[right]<key的情况,将arr[left]=arr[right],接下来,将转向left端,拿arr[left ]与key进行比较,如果arr[left]>key,则将arr[right]=arr[left],如果arr[left]<key,则只需要将left++,然后再进行arr[left]与key的比较。
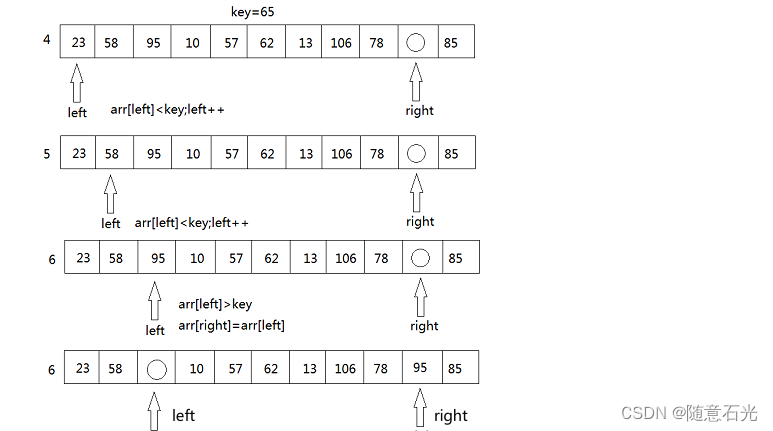
1.3.3 第三步
然后再移动right重复上述步骤

1.3.4 第四步
最后得到 {23 58 13 10 57 62} 65 {106 78 95 85},再对左子数列与右子数列进行同样的操作。最终得到一个有序的数列。
{23 58 13 10 57 62} 65 {106 78 95 85}
{10 13} 23 {58 57 62} 65 {85 78 95} 106
10 13 23 57 58 62 65 78 85 95 106
1.4 动画展示

- 首先,操作数列中的所有数字
- 在所有数字中选择一个数字作为排序的基准(pivot), pivot 通常是随机选择的,在这里为了演示方便,我们选择最右边的数字作为
pivot - 选取好 pivot 后,在操作数列中选择最左边的数字标记为 左标记 ,最右边的数字标记为 右标记
- 将左边的标记向右移动
- 当 左标记 达到超过 pivot 的数字时,停止移动
- 在这里,8 > 6 ,所以停止移动
- 然后将右边的标记向左移动
- 当 右标记 达到小于 pivot 的数字时,停止移动
- 在这里,4 > 6 ,所以停止移动
- 当左右标记停止时,更改标记的数字
- 因此,左标记 的作用是找到一个大于 pivot 的数字,右标记 的作用是找到一个小于 pivot 的数字
- 通过交换数字,可以在数列的左边收集小于 pivot 的数字集合,右边收集大于 pivot 的数字集合
- 交换之后,继续移动 左标记
- 在这里,9 > 6 ,所以停止移动
- 然后将右边的标记向左移动
- 当 右标记 碰撞到 左标记 时也停止移动
- 如果左右侧的标记停止时,并且都在同一个位置,将这个数字和 pivot 的数字交换
- 这就完成了第一次操作
- 小于 6 的都在 6 的左侧,大于 6 的都在 6 的右侧
- 然后递归对这分成的两部分都执行同样的操作
- 完成 快速排序
二:算法性能
2.1 时间复杂度
2.1.1 理想情况
如果足够理想,那我们期望每次都把数组都分成平均的两个部分,如果按照这样的理想情况分下去,我们最终能得到一个完全二叉树。如果排序 n 个数字,那么这个树的深度就是log2n+1,如果我们将比较 n 个数的耗时设置为 T(n),那我们可以得到如下的公式
T(n) ≤ 2T(n/2) + n,T(1) = 0
T(n) ≤ 2(2T(n/4)+n/2) + n = 4T(n/4) + 2n
T(n) ≤ 4(2T(n/8)+n/4) + 2n = 8T(n/8) + 3n
......
T(n) ≤ nT(1) + (log2n)×n = O(nlogn)
2.1.2 最坏情况
而在最坏的情况下,这个树是一个完全的斜树,只有左半边或者右半边。这时候我们的比较次数就变为
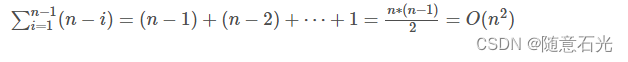
2.2 空间复杂度
2.2.1 原地排序
原地快排的空间占用是递归造成的栈空间的使用,最好情况下是递归(log_{2}n)次,所以空间复杂度为O(long2n)
,最坏情况下是递归 n-1 次,所以空间复杂度是O(n)。
2.2.2 非原地排序
对于非原地排序,每次递归都要声明一个总数为n的额外空间,所以空间复杂度变为原地排序的n倍,即最好情况下O(nlog2n)
,最差情况下(O(n^{2}))。
2.2.3 稳定性
不稳定。
三:代码实现
public class QuickSort {
public static void main(String[] args) {
int[] arr = {-9, 78, 0, 23, -567, 70, 23, 78, 958, 7, -15698, -56, 515};
long s = System.currentTimeMillis();
quickSort(arr, 0, arr.length - 1);
long e = System.currentTimeMillis();
System.out.println("arr=" + Arrays.toString(arr));
System.out.println("quickSort执行时间为:" + (e - s));
}
/**
* 快速排序
*
* @param arr 数组
* @param left 左侧索引
* @param right 右侧索引
*/
public static void quickSort(int[] arr, int left, int right) {
//左下标
int l = left;
//右下标
int r = right;
//pivot 中轴值
int pivot = arr[(left + right) / 2];
//临时变量。作为交换时使用
int temp = 0;
//while循环的目的是让比pivot值小的放到左边,比pivot值大的放到右边
while (l < r) {
//在pivot的左边一直找,找到大于等于pivot的值,才退出
while (arr[l] < pivot) {
l = l + 1;
}
//在pivot的右边一直找,找到小于等于pivot的值,才退出
while (arr[r] > pivot) {
r = r - 1;
}
//如果l >= r,说明pivot左右两边的值,符合左边小于等于pivot,左边大于等于pivot
if (l >= r) {
break;
}
//交换
temp = arr[l];
arr[l] = arr[r];
arr[r] = temp;
//如果交换完成以后,发现arr[l] = pivot,则需要将r--,前移一步
if (arr[l] == pivot) {
r = r - 1;
}
//如果交换完成以后,发现arr[r] = pivot,则需要将l++,后移一步
if (arr[r] == pivot) {
l = l + 1;
}
}
//如果l == r ,必须执行l++,r--操作,否则会出现栈内存溢出的情况
if (l == r) {
l = l + 1;
r = r - 1;
}
//向左递归
if (left < r) {
quickSort(arr, left, r);
}
//向右递归
if (right > l) {
quickSort(arr, l, right);
}
}
}