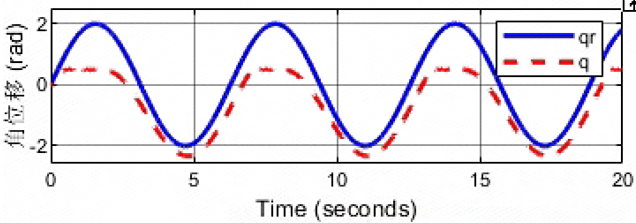
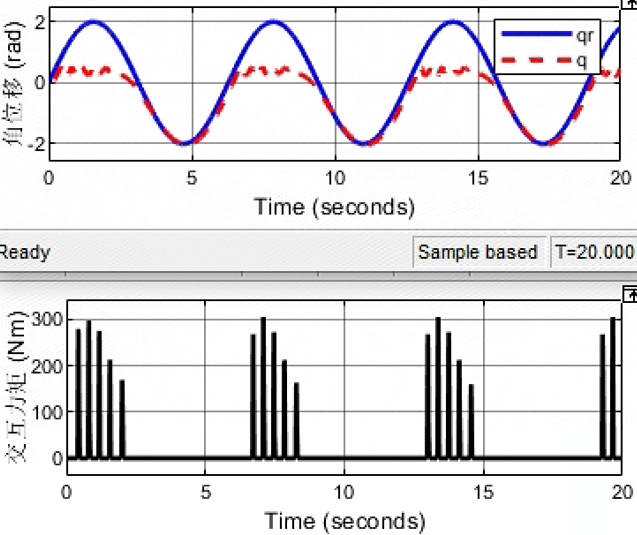
在阻抗控制下，当机器人接触刚性环境时，可能会出现振荡不稳定的情况。这可以通过调整机器人的阻抗参数来进行调节。

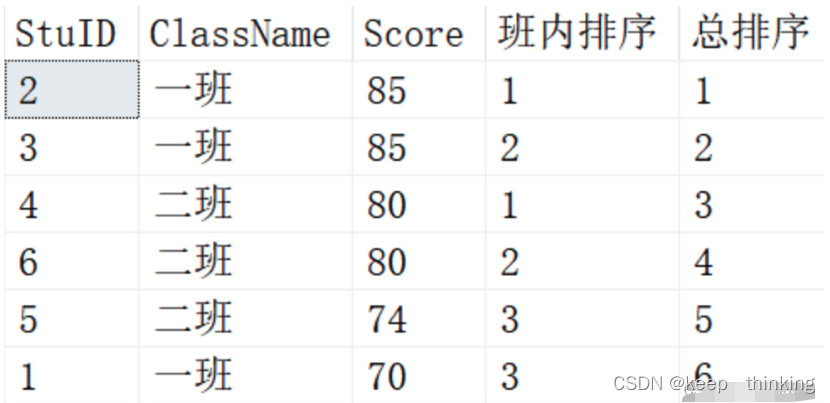
阻抗接触

       阻抗参数中的质量、阻尼和刚度都会对机器人控制系统的性能和稳定性产生重要影响。质量主要影响系统的惯性，从而影响响应速度和稳定性；阻尼则可以抑制系统的振荡，提高系统的稳定性；而刚度则表示系统抵抗变形的能力，过大的刚度可能导致系统不稳定。在设计和调整控制系统时，需要考虑这些参数的影响，并根据实际需求进行合理的选择和调整。  

在阻抗控制模式下，机器人接触刚性环境时会引起接触振荡，主要原因可以从阻抗参数的角度进行分析。首先，阻抗控制是一种基于系统动态特性的控制方法，通过调整系统的阻抗参数，实现对机器人与环境之间交互的精确控制。在接触刚性环境时，机器人会受到来自环境的反作用力，这种反作用力可能会引起机器人的振动。

1. 当阻尼参数较小时：机器人对外界力的响应比较缓慢，系统呈现出欠阻尼状态。此时，如果机器人受到来自环境的反作用力，由于阻尼较小，机器人无法迅速消耗这种能量，导致振荡的出现。
2. 当阻尼参数较大时：机器人对外界力的响应比较迅速，系统呈现出过阻尼状态。此时，虽然机器人能够迅速响应外界力，但由于阻尼较大，机器人对外界力的响应比较敏感，容易受到微小扰动的影响，也可能会出现振荡。
3. 当刚度参数较小时：机器人的刚度较低，对外界力的抵抗能力较弱。在接触刚性环境时，机器人可能会发生较大的变形，这种变形可能引起机器人的振动。
4. 当刚度参数较大时：机器人的刚度较高，对外界力的抵抗能力较强。在接触刚性环境时，机器人虽然不会发生较大的变形，但由于刚度较大，机器人对外界力的响应可能过于敏感，也可能会出现振荡。

       虽然这种振荡可能会对机器人的性能产生不利影响，但并不一定意味着机器人是不稳定的。在阻抗控制中，通常会使用一些稳定性判据来评估机器人的稳定性，如李雅普诺夫稳定性判据等。如果机器人在受到扰动后能够恢复稳定状态，那么这种振荡就不算是真正的不稳定性行为。

刚性环境为ke=10000

虚拟阻抗为：kd=100，bd=10，md=1

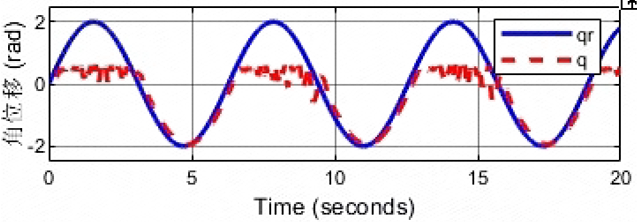
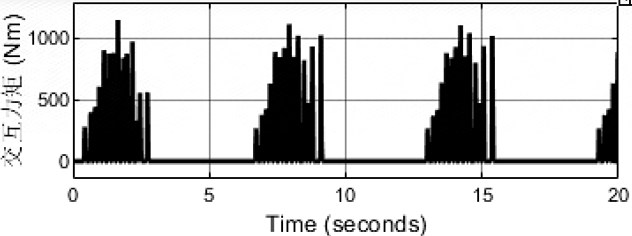
虚拟阻抗为：kd=100，bd=10，md=5

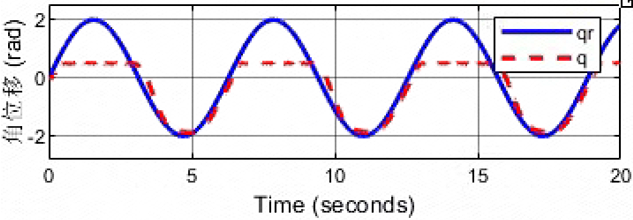
虚拟阻抗为：kd=100，bd=10，md=10

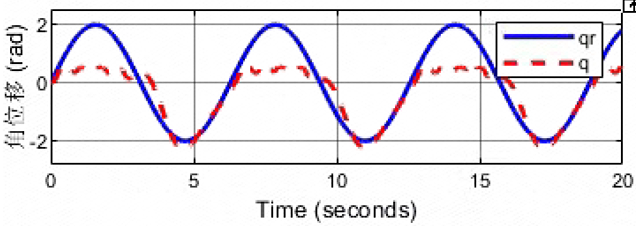
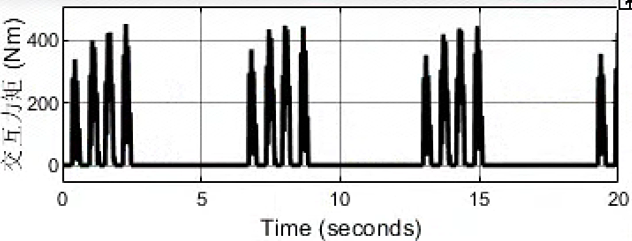
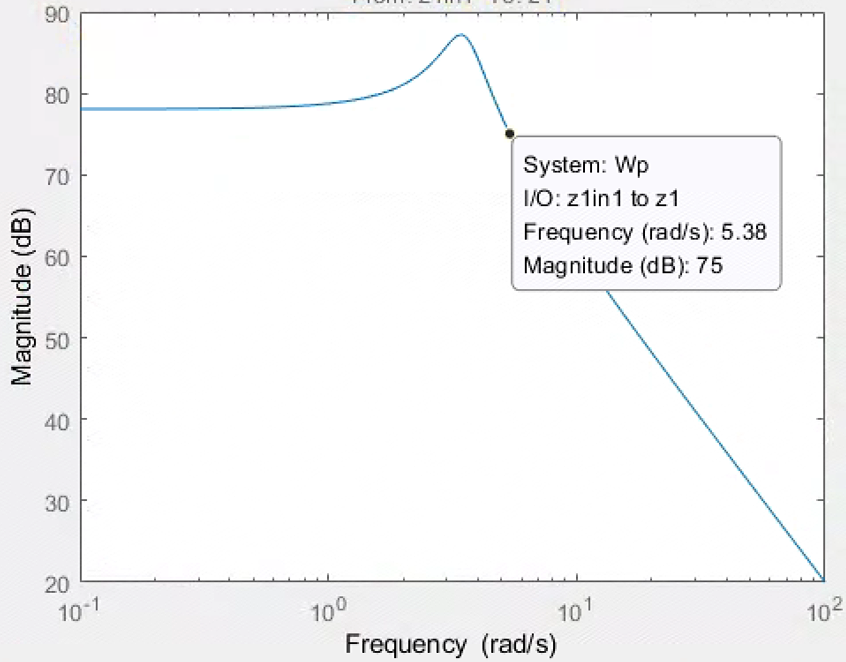
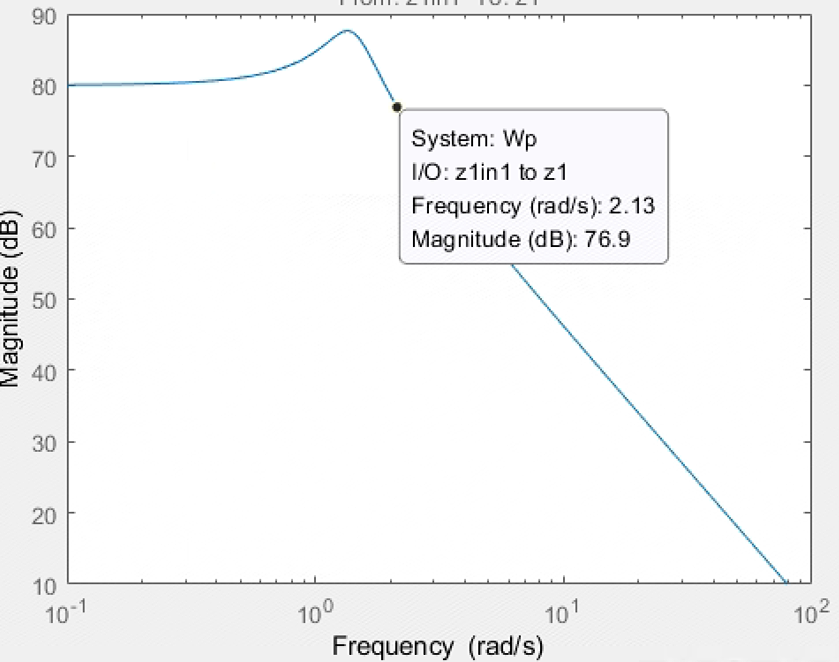
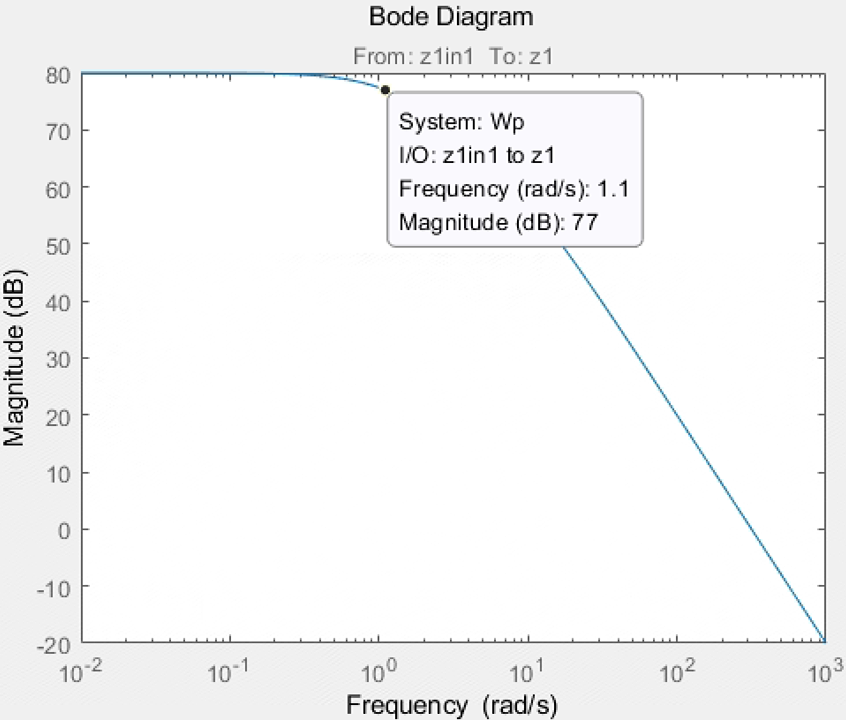
性能滤波函数的Bode图：

bode(1e5/(0.0005*s^2+5*s+1))

bode(5e4/(0.1*s^2+3*s+1))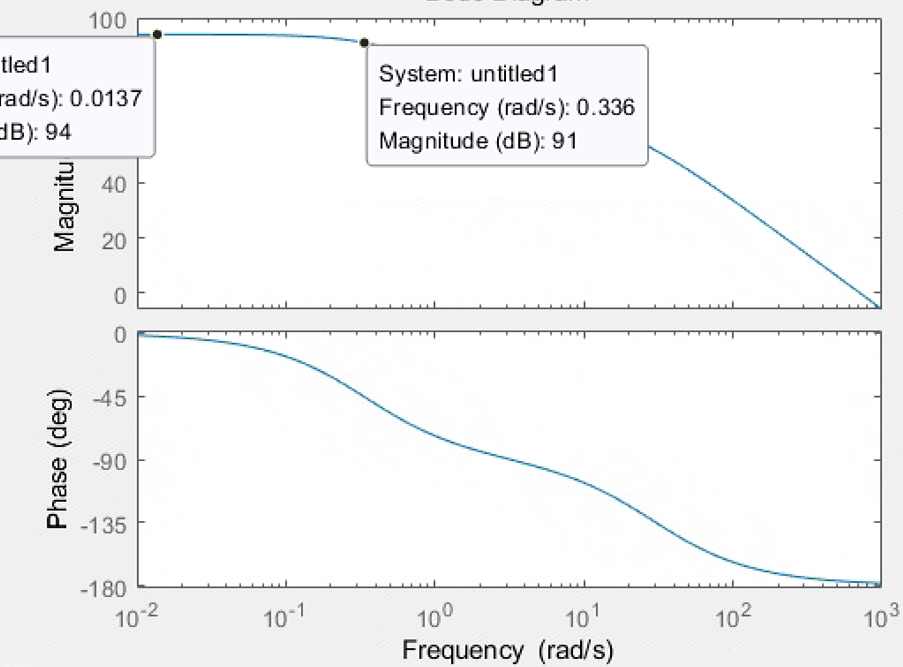

性能低通滤波调参

1e5/(1*s^2+3*s+1)

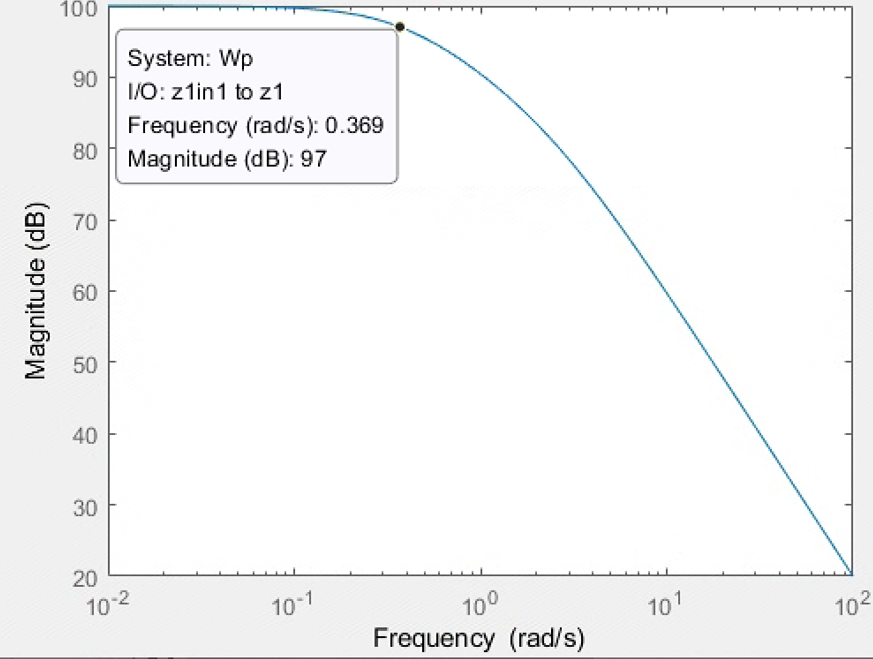
1e5/(1*s^2+5*s+1)

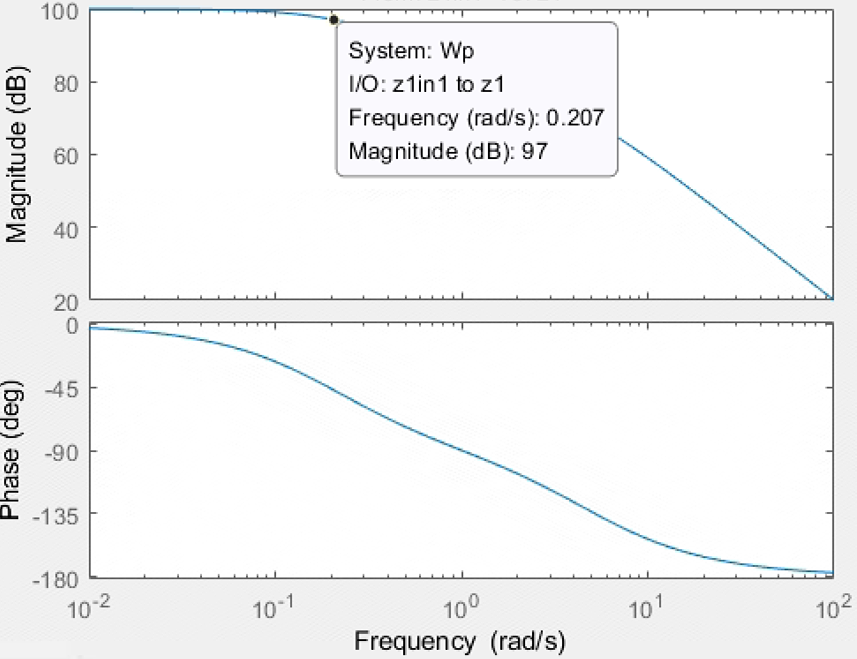
1e5/(1*s^2+10*s+1)

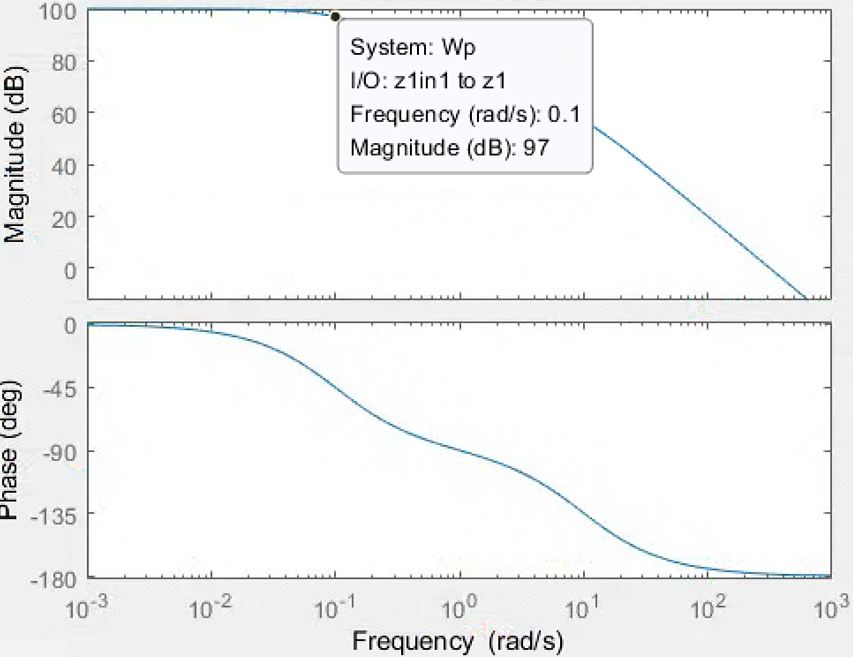
1e5/(2*s^2+3*s+1)

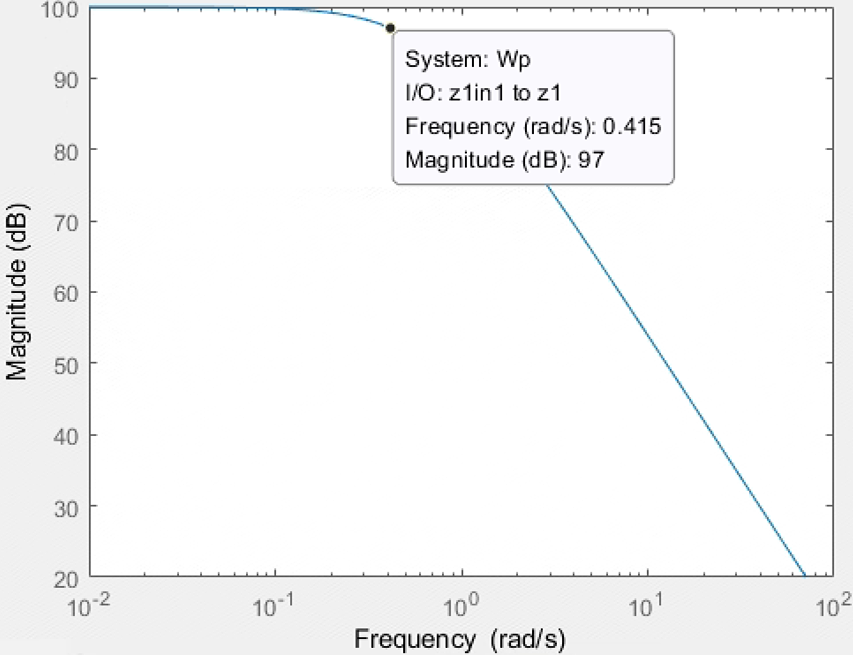
1e5/(2*s^2+1*s+1)

1e5/(3*s^2+1*s+1)

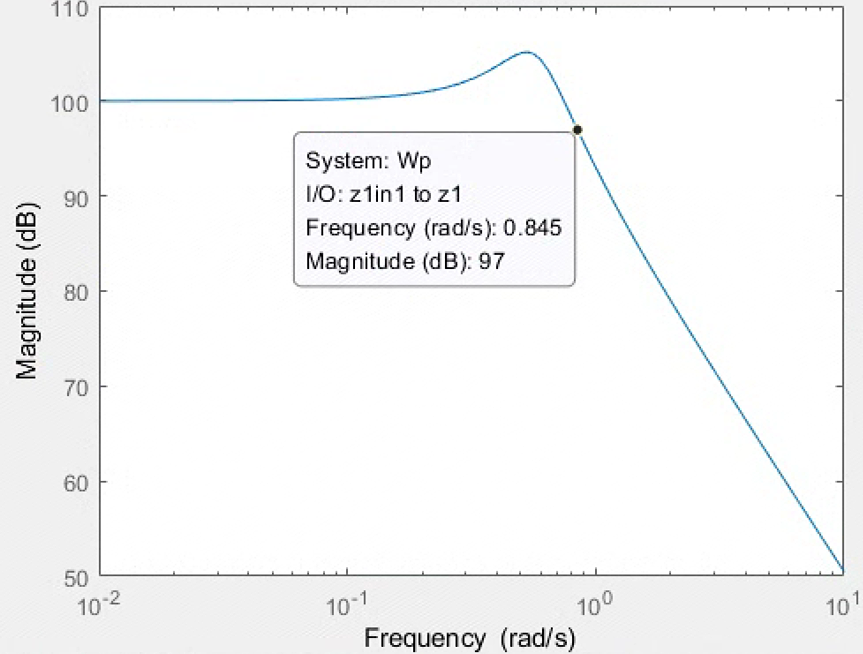
1e5/(4*s^2+1*s+1)

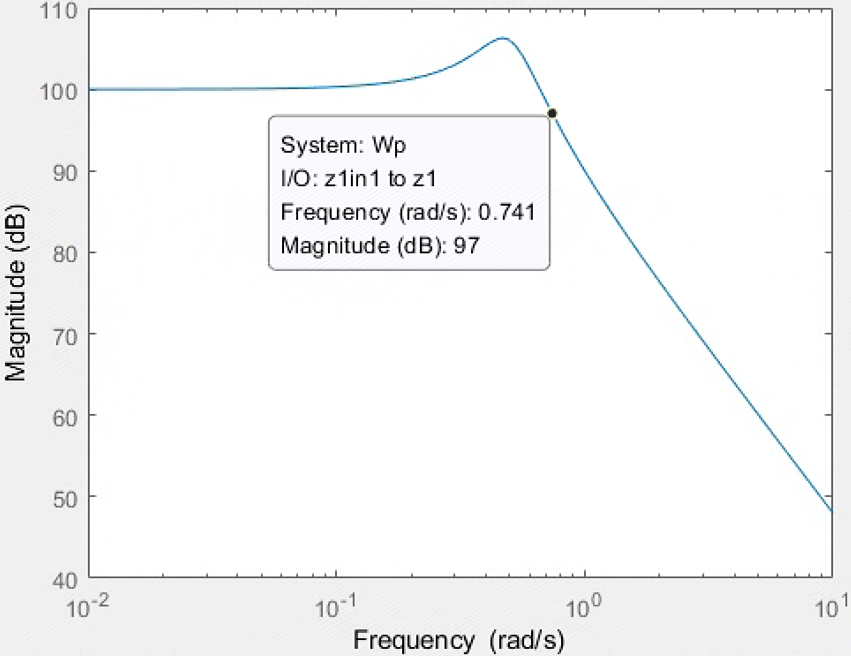
1e5/(1.5*s^2+0.9*s+1)

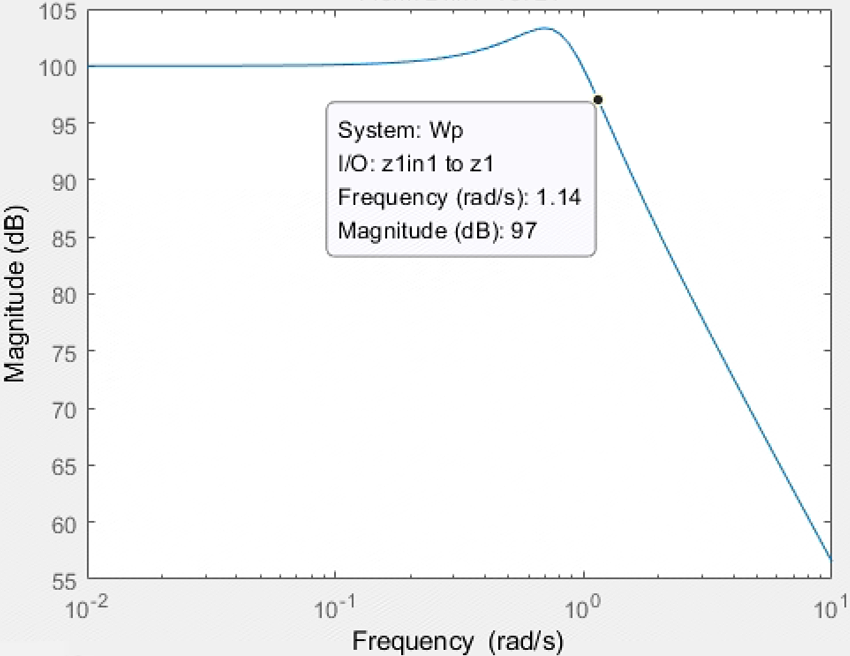
1e4/(1.2*s^2+0.8*s+1)

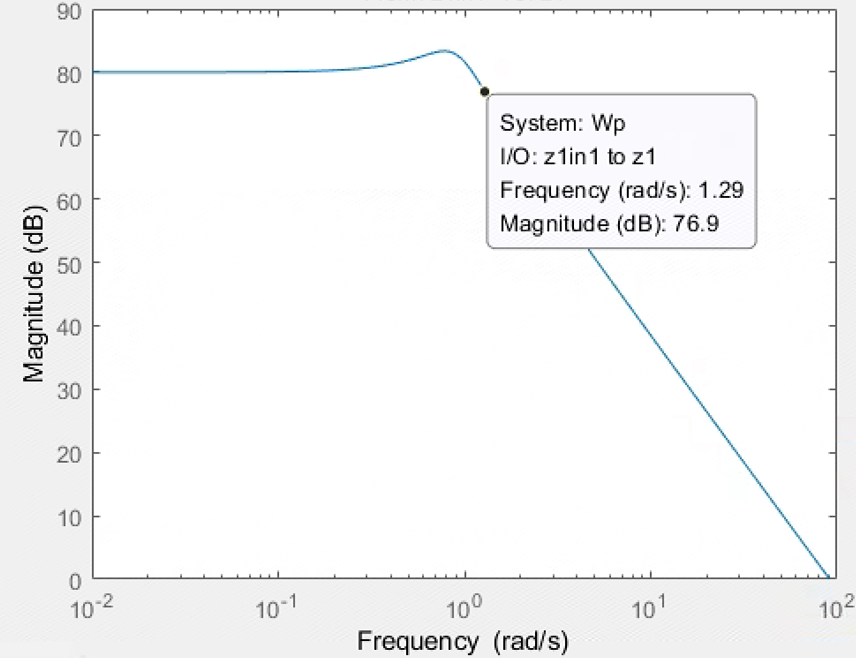
1e4/(0.1*s^2+0.8*s+1)

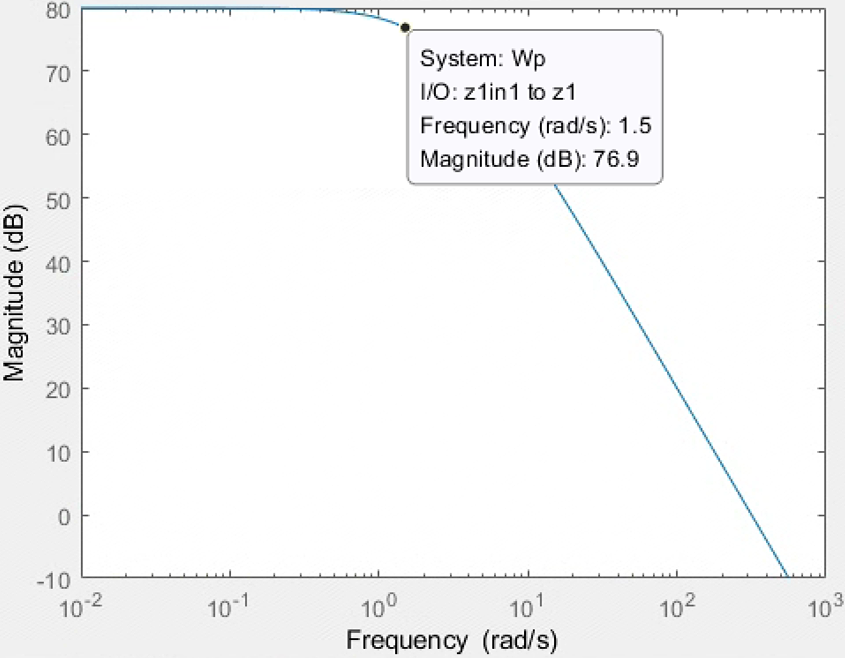
1e4/(0.1*s^2+0.1*s+1)

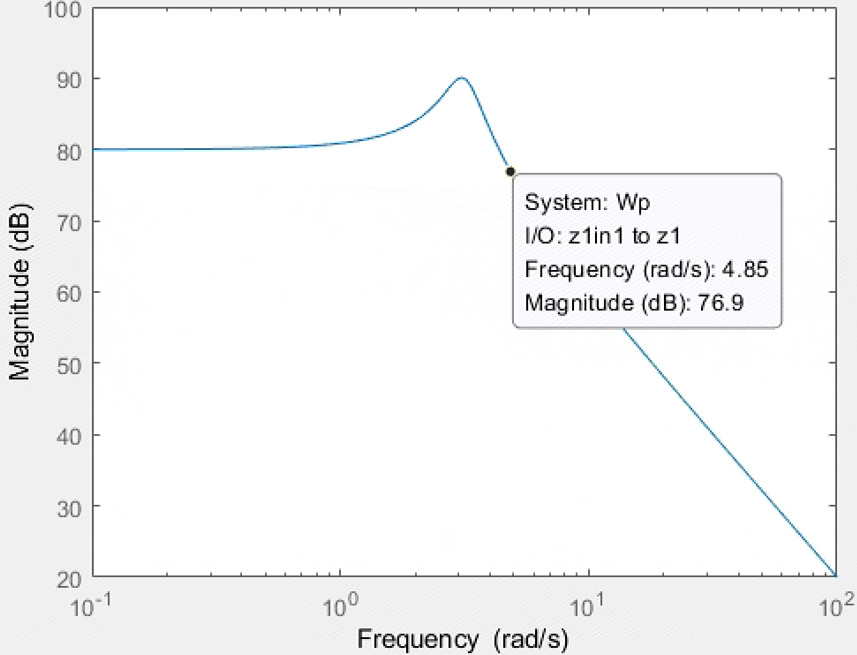
kd=10，bd=100

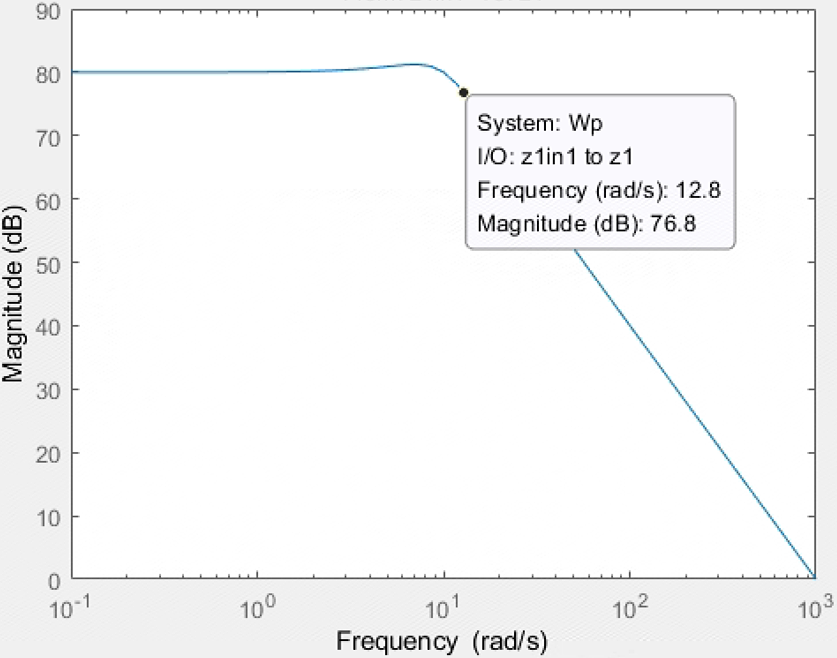
1e4/(0.01*s^2+0.1*s+1)

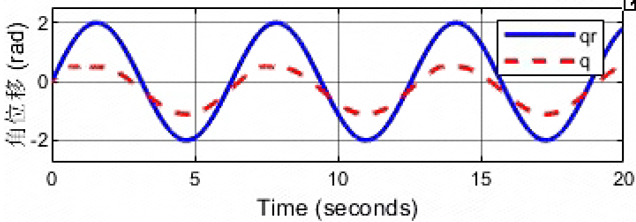
Wp = 1e3/(0.01*s^2+0.01*s+1)

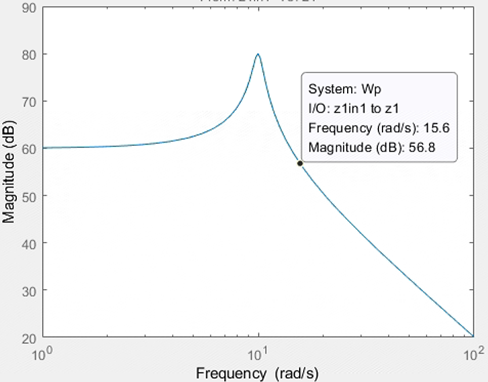
Wp = 1e3/(0.001*s^2+0.01*s+1);

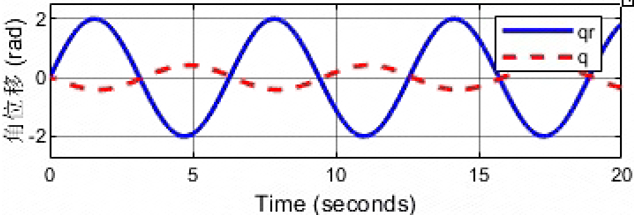
精度与鲁棒性的抉择！！！

1.5e4/(0.08*s^2+0.1*s+1)

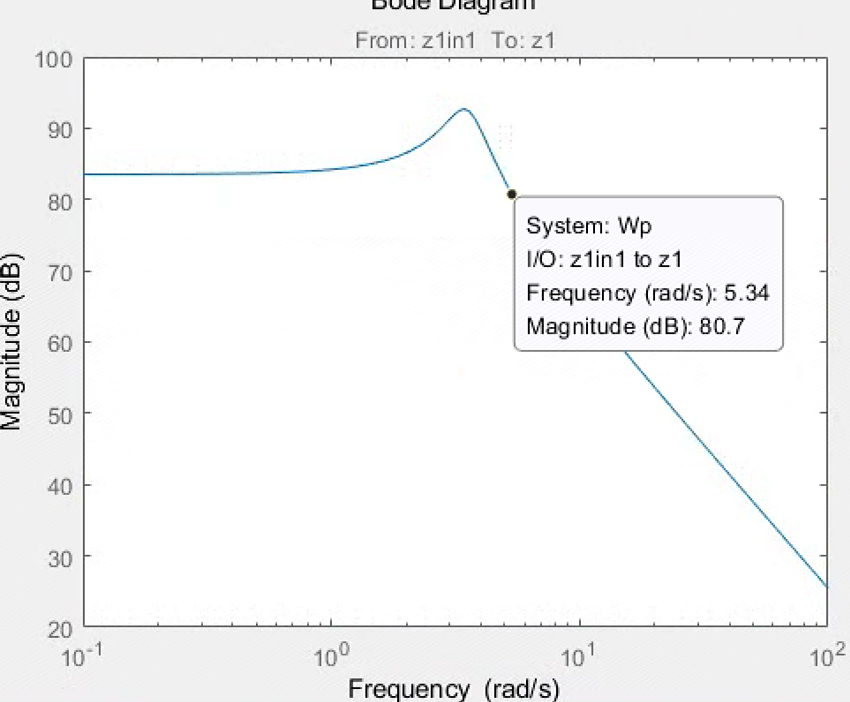
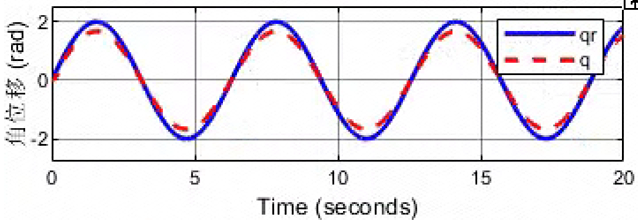
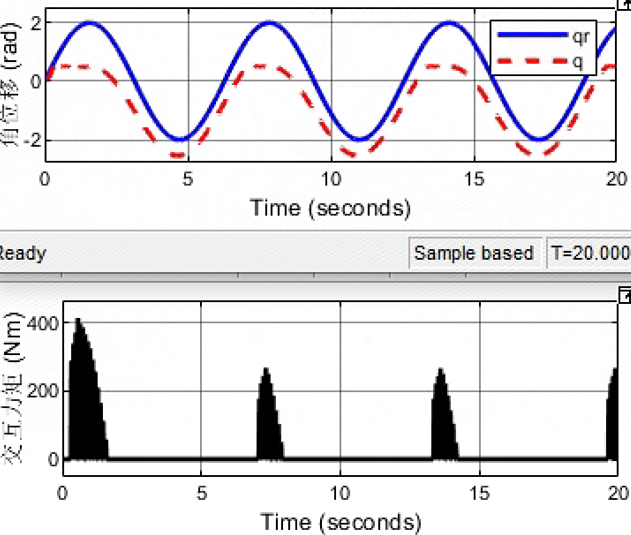
8e3/(0.08*s^2+0.1*s+1)

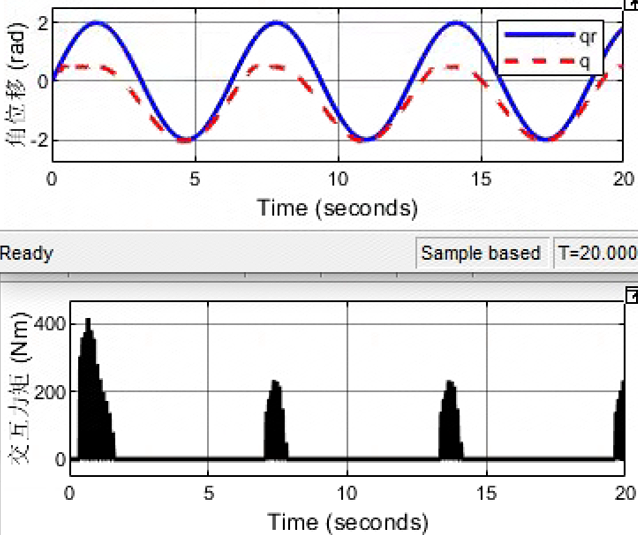
5e3/(0.08*s^2+0.08*s+1)

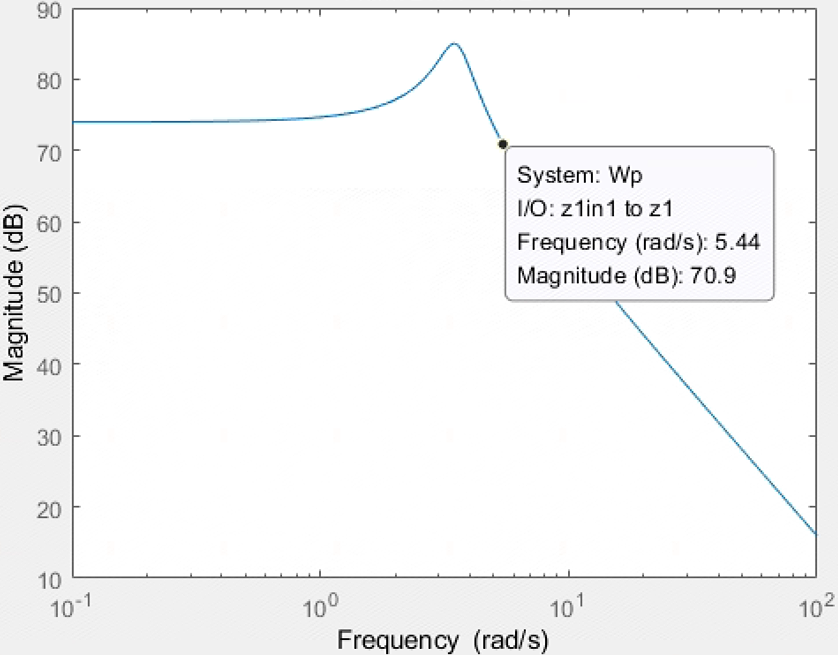
5e3/(0.1*s^2+0.01*s+1)

————————————————————————————————————————

低阻抗模式下的刚性接触

1e5/(0.0005*s^2+5*s+1)

纯弹簧接触

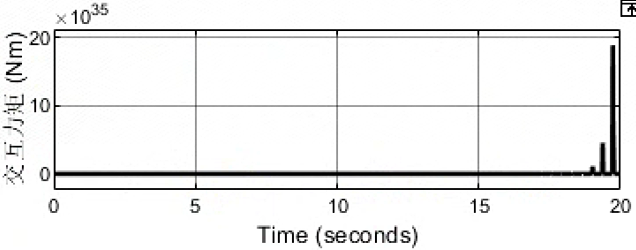
kd=10

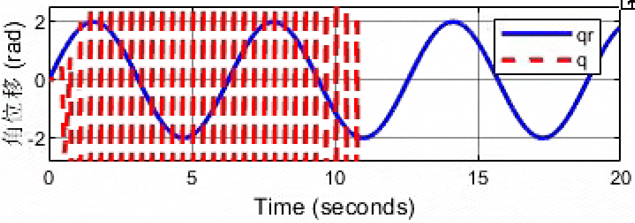
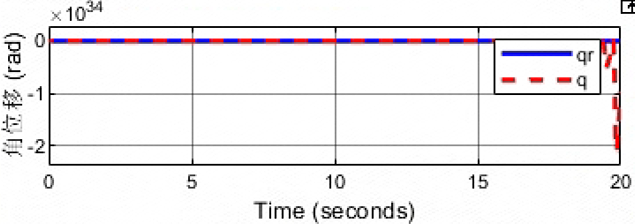
直接发散了！！！

kd=100

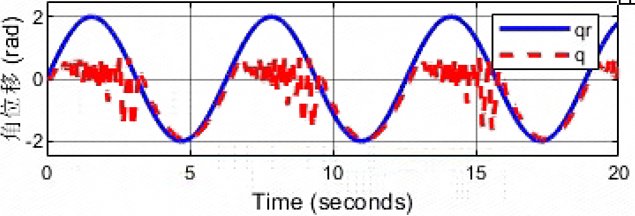
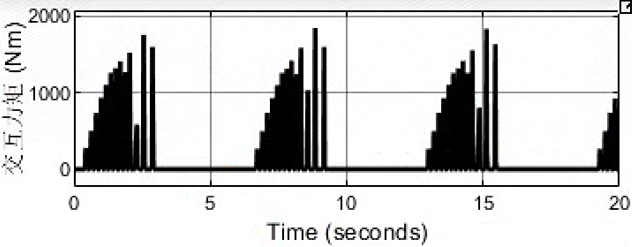
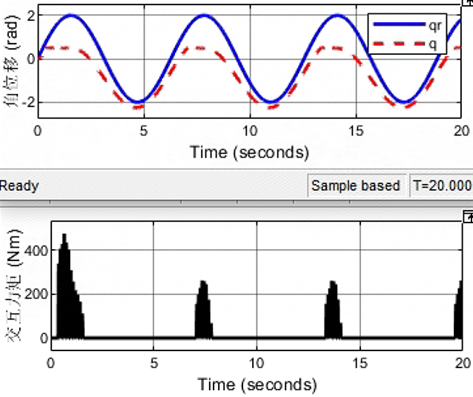
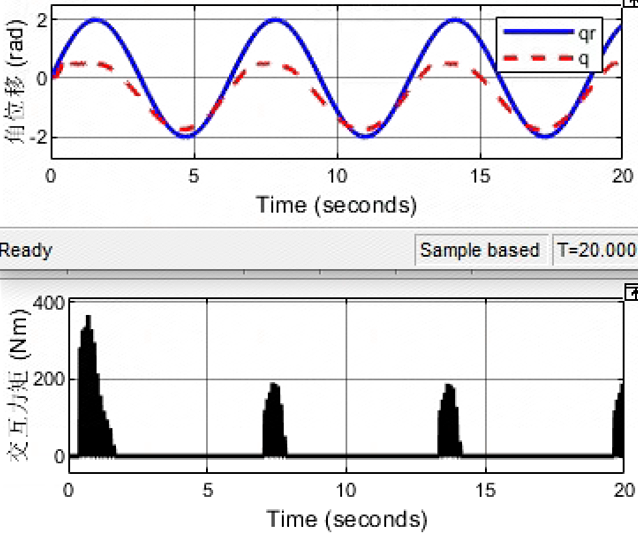
没有发散，但是刚性冲击过程振荡现象较为明显，这不是所期望的！！！

kd=1000

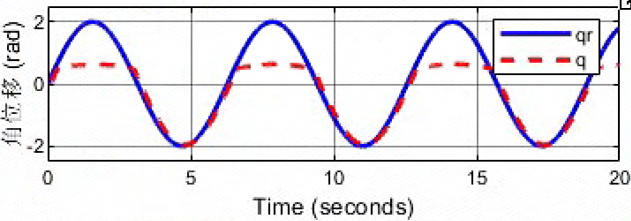
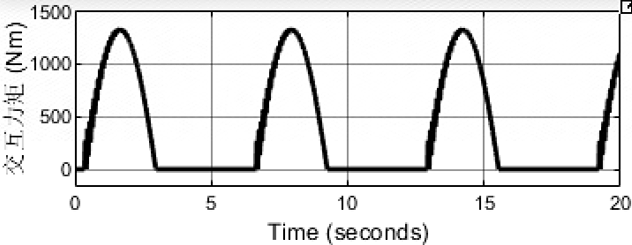
kd=10000

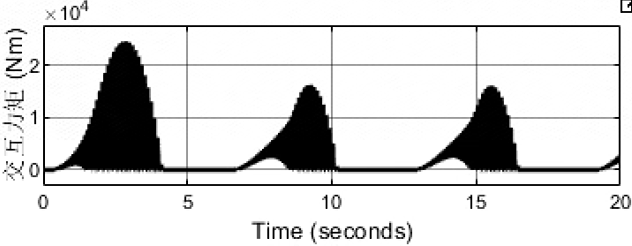
物极必反，刚度过大会引起较大振荡，意思是类似于两个纯刚体进行碰撞，势必会引起较大的振荡！！！

kd=100000

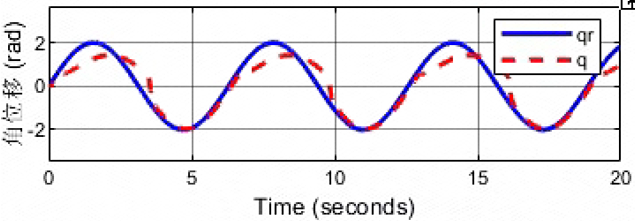
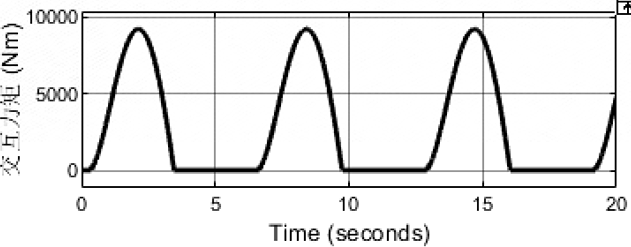
但阻抗实现性能就会很弱！！！

kd=1000000

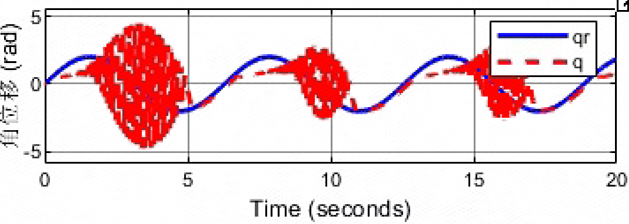
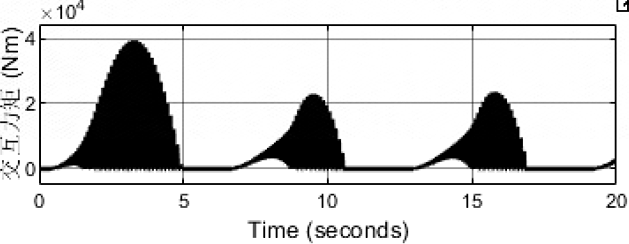
粘弹性接触

kd=10，bd=1

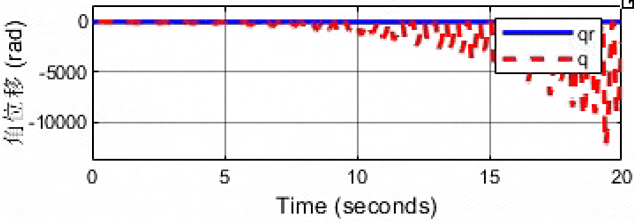
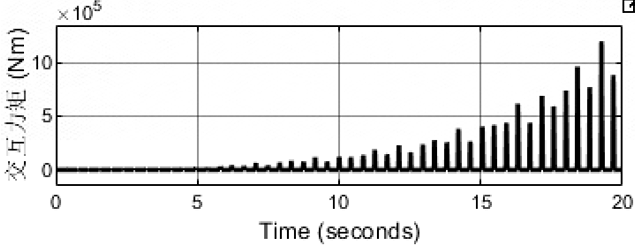
kd=10，bd=10

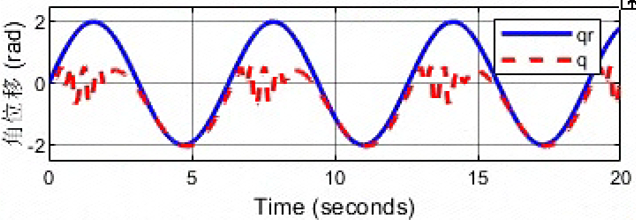
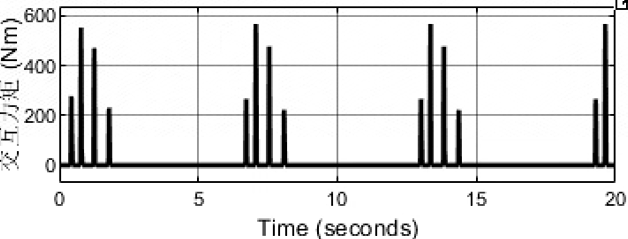
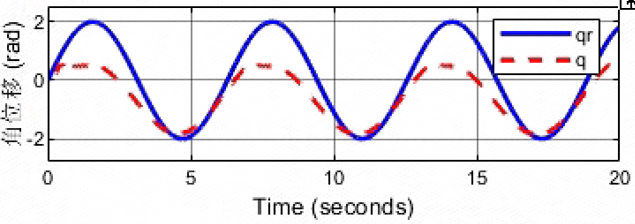
说明增大阻尼起到了减小震荡的作用。

kd=10，bd=15

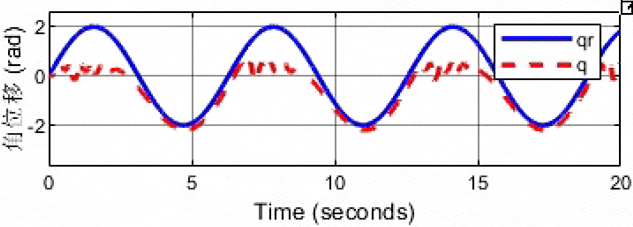
kd=10，bd=20

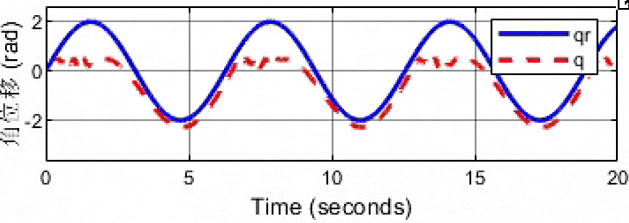
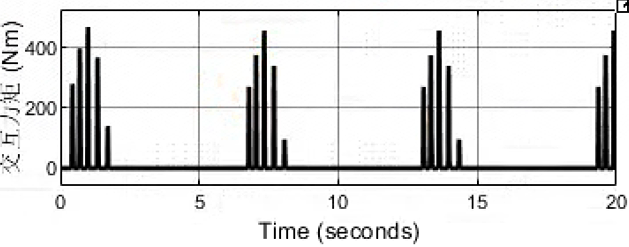
kd=10，bd=100

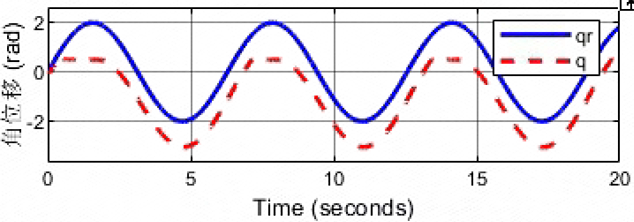
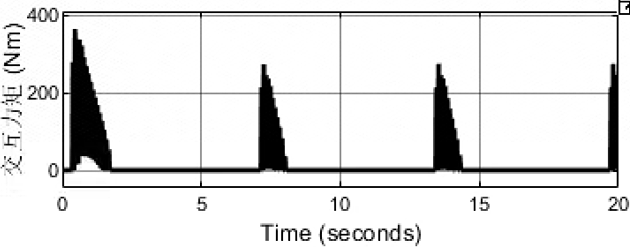
Kd = 100; Bd = 10 

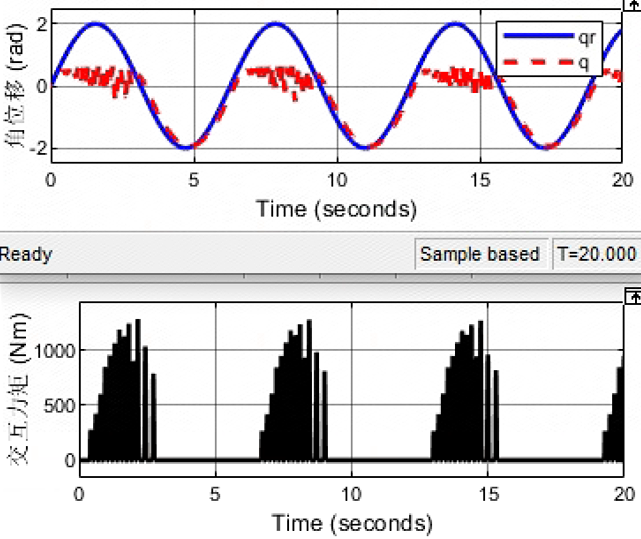
Kd = 100; Bd = 100

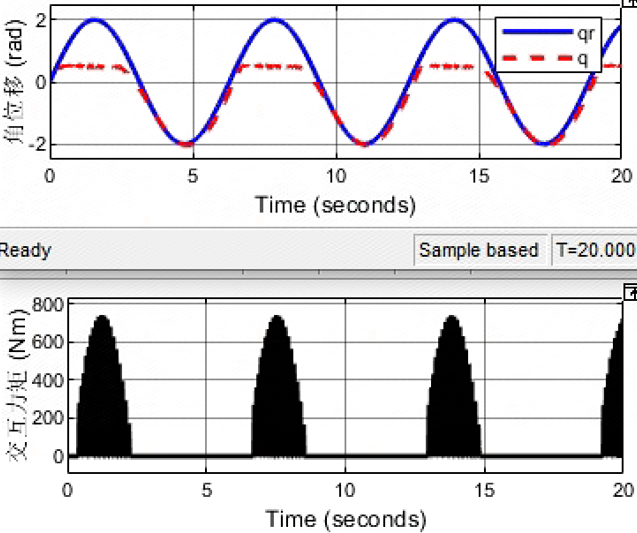
Kd = 100; Bd = 1000

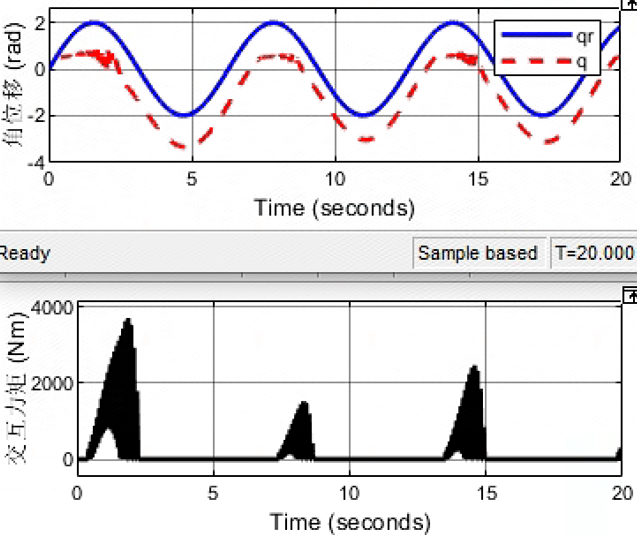
呈现质量-阻尼-弹簧动态

Kd = 10; Bd = 10 ; Md = 0.01;

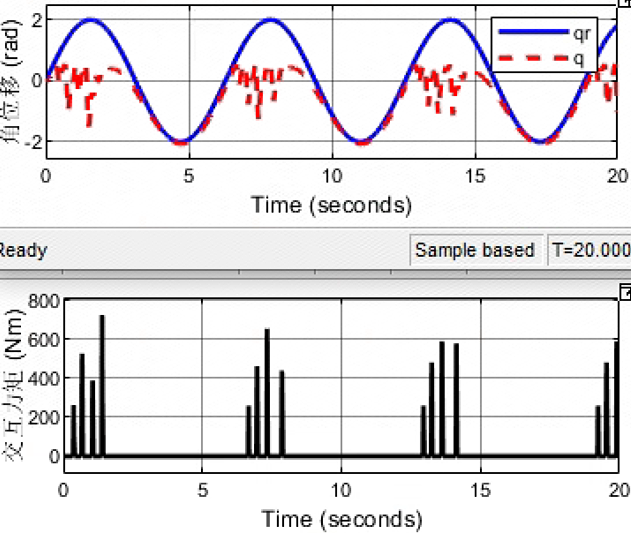
Kd = 10; Bd = 10 ; Md = 0.1;

Kd = 10; Bd = 10 ; Md = 1;

Kd = 10; Bd = 10 ; Md = 2;

————————————————————————————————————

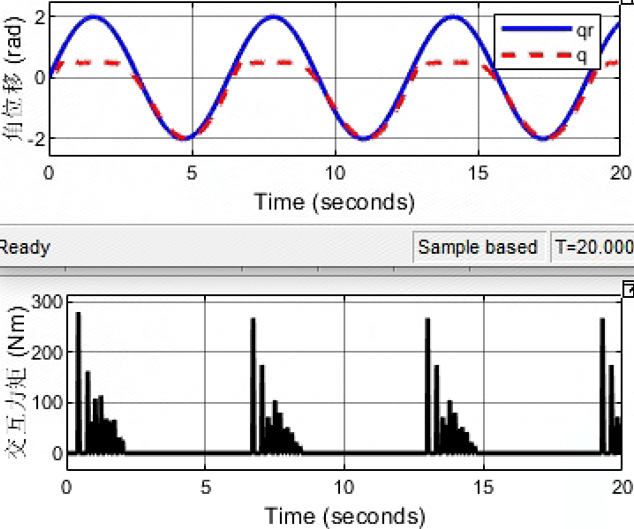
Kd = 100; Bd = 50 ; Md = 2;
 

1e4/(0.5*s^2+0.3*s+1)；9e3/(0.5*s^2+0.3*s+1)

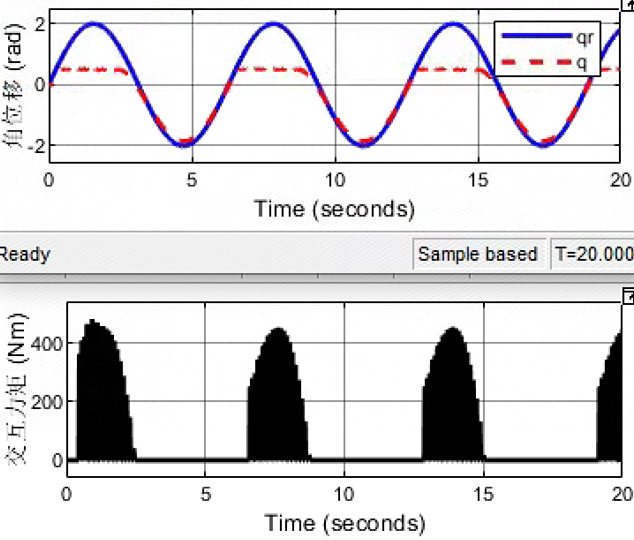
Kd = 10; Bd = 50 ; Md = 2;

1e4/(0.1*s^2+1*s+1)