🔥博客主页： A_SHOWY
🎥系列专栏：力扣刷题总结录 数据结构 云计算 数字图像处理
| 28.找出字符串中第一个匹配项的下标 | mid | 经典KMP |
| 4593重复的子字符串 | mid | 可以使用滑动窗口或者KMP |
KMP章节难度较大，需要深入理解其中的底层原理，单纯背代码不可靠
一、KMP方法总结
（1）KMP能解决的问题
KMP主要应用在字符串匹配上
（2）前缀和后缀
前缀：包含首字母不包含尾字母的所有子串
例如：
字符串aabaaf
前缀： a
aa
aab
aaba
aabaa
aabaaf ×后缀：包含尾字母而不包含首字母的所有子串
字符串aabaaf
后缀： f
af
aaf
baaf
abaaf
aabaaf ×（3）最长相等的前后缀
模式串的前缀表
字符串aabaaf
最长相等前后缀：
a 0
aa 1
aab 0
aaba 1
aabaa 2
aabaaf 0
所以前缀表是010120
所以要跳到最长的相等前后缀的后面去接着匹配
（4）前缀表原理
模式串与前缀表对应位置的数字表示的是：下标i之前的字符串中，有多大长度的相同前后缀，所以当找到不匹配的位置时，要看前一个字符的前缀表的数值，因为要找前一个字符的最长相同的前后缀，前一个字符的前缀表的数值是2， 所以把下标移动到下标2的位置继续比配。next（prefix）数组：遇到冲突后，要回退到的下一个位置
最重要的一点（理解KMP的核心）：为什么使用前缀表可以告诉我们匹配失败之后跳到哪里重新匹配？
假设在下标为5的部分不匹配了，下标5之前的这部分字符串最长相等的前后缀是aa，找到了最长的相等前后缀，匹配失败的地方是后缀子串的后面，那么找到与其相等的前缀部分就可以继续匹配了。
（5）前缀表代码实现
1.求next数组方式有很多 （比如原封不动【如果遇到冲突了，就找这个前缀表数组的前一位作为下标】，有的全部右移【初始值为-1，冲突这个位置对应下标】，有的全部减去1【不推荐 】），但是next数组的核心是遇到冲突了要向前回退
2.i指向了后缀末尾，j指向了前缀末尾，还代表i（包括i）之前的子串的最长相等前后缀的长度（这里难点就是j的双层含义），他非常像一个递归的过程
3.具体步骤可以分为四步：初始化 讨论处理前后缀不相同的时候 处理前后缀相同的时候 给next数组赋值，就能得到模式串的前缀表
- 首先是初始化，对于 i和j的初始化以及next【0】的初始化，那么j我们初始化为-1，前面提到这只是其中的一种表现形式也就是串整体右移，那么i选择1（i肯定不能是0），next【i】表示i之前最长前后缀的长度，其实也就是j对于i的初始化我们放在后边的循环里
int j = -1;
next[0] = j;- 其次就是讨论前后缀不相同的情况，比较s【i】和s【j+1】是否相同，如果不同，那么就要回退，由于next【j】记录着j之前子串相同前后缀的长度，就要找j+1前一个元素在next数组的值（next【j】），注意向前回退是一个持续的过程，所以用while如果不匹配就一直回退
for(int i = 0; i < s.size(); s++){
while(j>=0 && s[i] != s[j+1]){
//向前回退
j = next[j];
}
}- 然后处理前后缀相同的情况,如果s【i】和s【j+1】相同，，就要同时移动i和j，并且，讲j赋值给next【i】
if (s[i] == s[j + 1]) { // 找到相同的前后缀
j++;
}
next[i] = j;所以完整版本的 代码如下：
void getNext(int* next, const string& s){
int j = -1;
next[0] = j;
for(int i = 1; i < s.size(); i++) { // 注意i从1开始
while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
j = next[j]; // 向前回退
}
if (s[i] == s[j + 1]) { // 找到相同的前后缀
j++;
}
next[i] = j; // 将j（前缀的长度）赋给next[i]
}
}二、经典题目
（1）28.找出字符串中第一个匹配项的下标
28. 找出字符串中第一个匹配项的下标
https://leetcode.cn/problems/find-the-index-of-the-first-occurrence-in-a-string/其实这个题目可以分成两个部分，是一个经典的字符串匹配题目，肯定是用我们刚刚学过的KMP算法来完成。那么所谓分成两个部分解体，第一部分就是构造NEXT数组，第二部分就是运用这个前缀表进行一个匹配的问题，那么第一部分的构造前缀表（NEXT数组）已经写完了，下面我们来写匹配过程的代码。注意我们一直用的是全体-1操作后的NEXT数组，在文本串haystack里面查找是否出现过模式串needle。
int strStr(string haystack, string needle) {
int j = -1;
int next[needle.size()];
getNext(next,needle);
for(int i = 0; i< haystack.size();i++)//匹配过程中，next数组的使用从索引0开始
{
while(j >= 0 && haystack[i] != needle[j+1]){
j = next[j];
}
if(haystack[i] == needle[j+1]){
j++;
}
if(j == needle.size() -1){//j到了末尾
return (i-needle.size() +1);//返回首部
}
}
return -1;
}这里有几个要注意的点，第一个是i的初始值，匹配过程中，next数组的使用从索引0开始，在构造next数组的时候，0已经给了初始值了，所以从1开始。
然后就是如何判断是否包含呢，当i走到了needle的末尾的时候，说明存在匹配，返回首部的数值即可，所以完整的代码实现为
class Solution {
public:
void getNext(int* next, string& s){
int j = -1;
next[0] = j;//初始化
for(int i =1; i < s.size();i++)//初始化，i从1开始
{
while(j >= 0 && s[i] != s[j+1]){//如果不想等
j = next[j];//j就回退，这里有点像递归
}
if(s[i] == s[j+1]){
j++;
}
next[i] = j;//最后给next数组的i坐标赋值
}
}
int strStr(string haystack, string needle) {
int j = -1;
int next[needle.size()];
getNext(next,needle);
for(int i = 0; i< haystack.size();i++)//匹配过程中，next数组的使用从索引0开始
{
while(j >= 0 && haystack[i] != needle[j+1]){
j = next[j];
}
if(haystack[i] == needle[j+1]){
j++;
}
if(j == needle.size() -1){//j到了末尾
return (i-needle.size() +1);//返回首部
}
}
return -1;
}
};（2）459.重复的子字符串
459. 重复的子字符串https://leetcode.cn/problems/repeated-substring-pattern/
方法一：滑动窗口
当一个字符串内部由重复的子串组成，也就是由前后相同的子串组成。那么既然前面有相同的子串，后面有相同的子串，用 s + s，这样组成的字符串中，后面的子串做前串，前面的子串做后串，就一定还能组成一个s。
所以总体的思路为(个人认为很神奇的思路)：只要两个s拼接在一起，里面还出现一个s的话，就说明是由重复子串组成。但是注意要去除s+s的字符串的首尾位置，不然判断没有意义。
class Solution {
public:
bool repeatedSubstringPattern(string s) {
string t = s + s;
//掐头去尾
t.erase(t.begin());
t.erase(t.end() -1);//注意是end-1，应为t.end，返回指向t末尾下一个位置的迭代器
if(t.find(s) != std::string::npos)//指的是字符串中未找到指定内容时的特殊返回值
return true;
return false;
}
};方法二：KMP算法
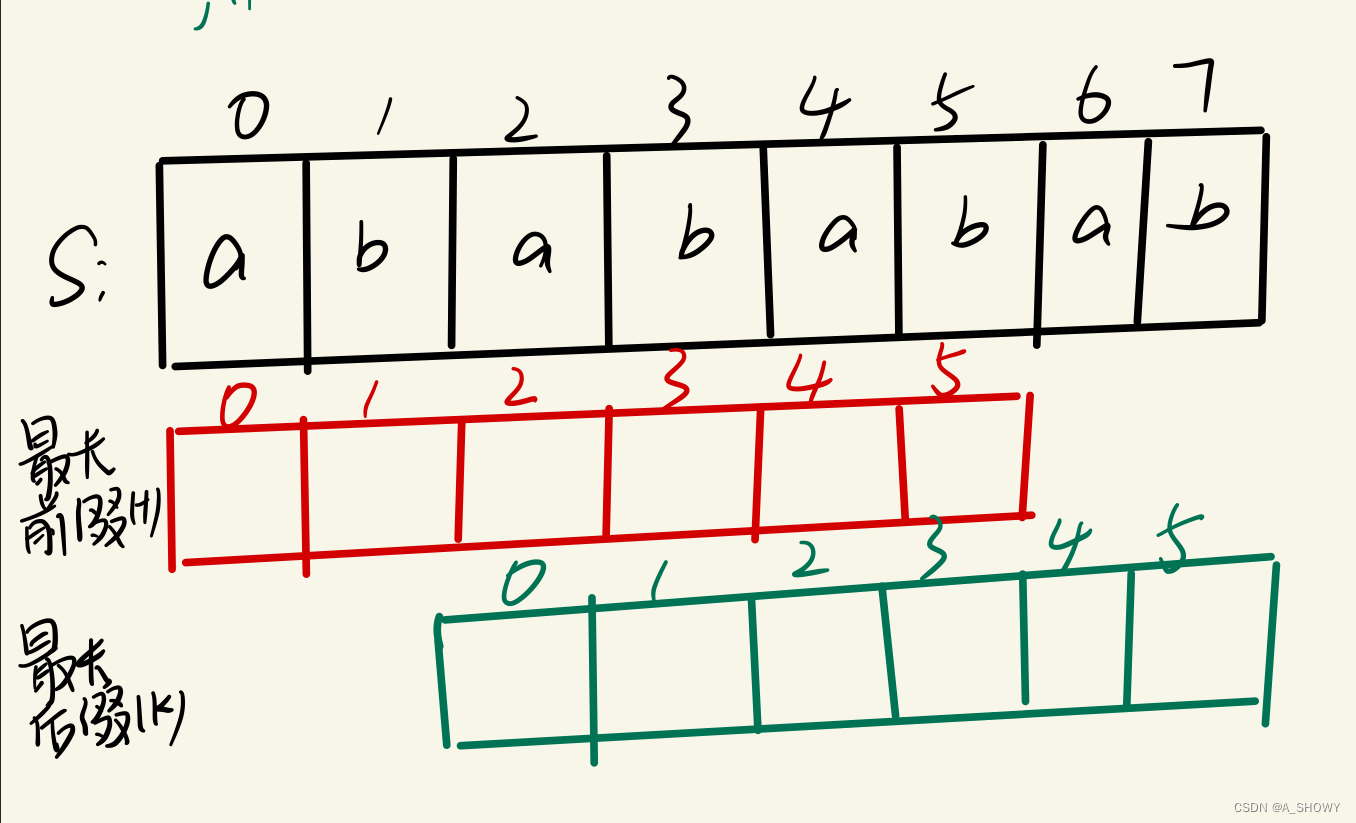
为什么可以使用KMP
步骤一：因为 这是相等的前缀和后缀，t[0] 与 k[0]相同， t[1] 与 k[1]相同，所以 s[0] 一定和 s[2]相同，s[1] 一定和 s[3]相同，即：，s[0]s[1]与s[2]s[3]相同 。
步骤二： 因为在同一个字符串位置，所以 t[2] 与 k[0]相同，t[3] 与 k[1]相同。
步骤三： 因为 这是相等的前缀和后缀，t[2] 与 k[2]相同 ，t[3]与k[3] 相同，所以，s[2]一定和s[4]相同，s[3]一定和s[5]相同，即：s[2]s[3] 与 s[4]s[5]相同。
步骤四：循环往复。
结论：在由重复子串组成的字符串中，最长前后缀不包含的子串就是最小重复子串
最长相等前后缀的长度为：next[len - 1] + 1。(这里的next数组是以统一减一的方式计算的，因此需要+1，如果len % (len - (next[len - 1] + 1)) == 0 ，则说明数组的长度正好可以被 (数组长度-最长相等前后缀的长度) 整除 ，说明该字符串有重复的子字符串。 （仍然是很神奇的思路）
class Solution {
public:
void getNext (int* next, const string& s){
next[0] = -1;
int j = -1;
for(int i = 1;i < s.size(); i++){
while(j >= 0 && s[i] != s[j + 1]) {
j = next[j];
}
if(s[i] == s[j + 1]) {
j++;
}
next[i] = j;
}
}
bool repeatedSubstringPattern (string s) {
if (s.size() == 0) {
return false;
}
int next[s.size()];
getNext(next, s);
int len = s.size();
if (next[len - 1] != -1 && len % (len - (next[len - 1] + 1)) == 0) {
return true;
}
return false;
}
};
