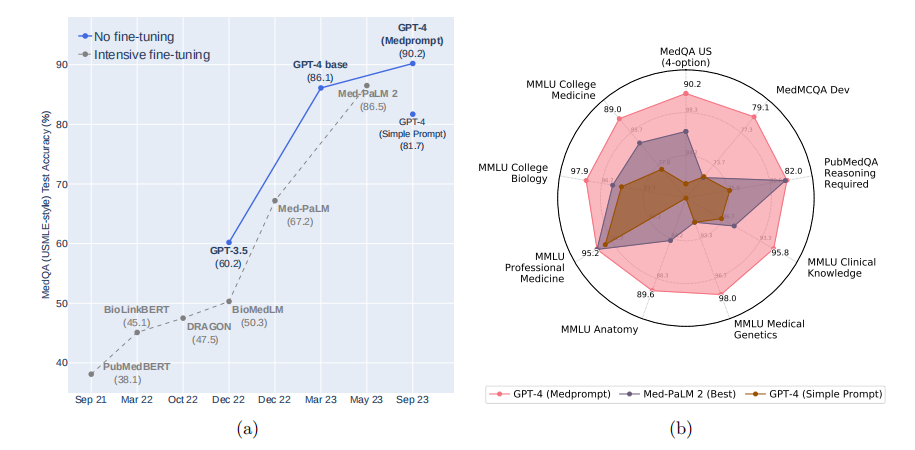
DH介绍
Diffie-Hellman密钥协议算法是一种确保共享密钥安全穿越不安全网络的方法。
这个机制的巧妙在于需要安全通信的双方可以用这个方法确定对称密钥,然后可以用这个密钥进行加密和解密。
但是注意,这个密钥交换协议 只能用于密钥的交换,而不能进行消息的加密和解密。 双方确定要用的密钥后,要使用其他对称密钥操作加密算法实际加密和解密消息。
这种秘钥交换技术的目的在于使两个用户安全的协商一个会话密钥。
DH密钥交换流程
- 步骤1:Alice和Bob共同确定公开的大素数 P P P和一个整数 G G G,其中 G G G是 P P P的原根
- 步骤2:Alice选取一个秘密整数 a a a作为私钥,然后对 a a a进行幂模计算,得到公钥 A A A: A = G a m o d P A=G^a~\mathrm{mod}~P A=Ga mod P,然后将 A A A发给Bob
- 步骤3:和Alice一样,Bob选取一个秘密整数 b b b作为私钥,然后对 b b b进行幂模计算,得到公钥 B B B: B = G b m o d P B=G^b~\mathrm{mod}~P B=Gb mod P,然后将 B B B发给Alice【 A , B A, B A,B就是所谓的Diffie-Hellman公开值】
- Alice计算密钥 K 1 = B a m o d P K_1=B^a~\mathrm{mod}~P K1=Ba mod P
- 和Alice一样,Bob计算密钥 K 2 = A b m o d P K_2=A^b~\mathrm{mod}~P K2=Ab mod P
- K 1 = B a m o d P = ( G b ) a m o d P = G a b m o d P , K 2 = A b m o d P = ( G a ) b m o d P = G a b m o d P K_1=B^a~\mathrm{mod}~P=(G^b)^a~\mathrm{mod}~P=G^{ab}~\mathrm{mod}~P, K_2=A^b~\mathrm{mod}~P=(G^a)^b~\mathrm{mod}~P=G^{ab}~\mathrm{mod}~P K1=Ba mod P=(Gb)a mod P=Gab mod P,K2=Ab mod P=(Ga)b mod P=Gab mod P,因此, K 1 = K 2 K_1=K_2 K1=K2【 K 1 , K 2 K_1, K_2 K1,K2就是所谓的共享密钥】

安全性分析
对于幂模运算 c = b e m o d m c=b^e~\mathrm{mod}~m c=be mod m,只要给定 b , e , m b, e, m b,e,m,求模幂的过程是非常高效的。另一方面,当 m m m是大素数时,给定 b , c , m b, c, m b,c,m,求指数 e e e的过程是很难的【称为离散对数的难题】。这种单向函数的特性使模幂运算被多次用于密码算法中。
DH通信过程可见,只有 G , P , A , B G, P, A, B G,P,A,B会在传输,而 a , b a, b a,b是不会传输的。同时,因为离散对数的难解,当 G , P G, P G,P选的足够大时,通过 A , B A, B A,B分别推算 a , b a, b a,b是极其困难的。进而,破解出最终的对称密钥K也是极其困难的。