二叉树结点个数、叶子结点个数、树的高度、第k层结点个数的计算（C语言）

前言

分治算法

模拟二叉树代码

结点个数计算

错误方法

不便利方法

基于分治思想的方法

叶子结点个数

树的高度

第k层结点的个数

前言

在链式二叉树的前序、中序、后续遍历中我们模拟了一棵二叉树，并实现了它的前、中、后序遍历，现在我们来解决设计与二叉树相关的计算问题。

分治算法

概念：是一种将问题划分为更小的子问题，并通过解决子问题来解决原始问题的算法设计策略

分治算法的基本思想：

分解：将原始问题划分成若干个规模较小且相互独立的子问题。这里关键是要找到一个适当的方式将原始问题切割成更小规模的子问题，使得每个子问题都与原始问题具有相同或类似结构。
解决：递归地求解各个子问题。对于规模较小而直接可求解的情况，直接给出答案；对于规模较大而无法直接求解时，则继续应用该算法来进一步划分为更小的子问题并进行求解。
合并：将各个子结果合并成最终结果。在所有子任务都被独立地处理和求得结果之后，需要把这些局部结果合并起来以获得整体上正确且有效率的最终输出。

可以应用分治算法来解决的问题的特点：

1、原问题可以分解为多个子问题

子问题与原问题相比，只是问题的规模有所降低，其结构和求解方法与原问题相同或相似

2、原问题在分解过程中，递归地求解子问题

由于递归都必须有一个终止条件，故当分解后的子问题规模足够小时，应能够直接求解

3、在求解并得到各个子问题的解后

应能够采用某种方式、方法合并或构造出原问题的解

结论：不难发现，在分治策略中，由于子问题与原问题在结构和解法上的相似性，用分治方法解决的问题，大都采用了递归的形式🥰

模拟二叉树代码

#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
typedef int BTDataType;
 
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}TreeNode;
 
TreeNode* BuyTreeNode(int x)
{
	TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));
	assert(node);
 
	node->data = x;
	node->left = NULL;
	node->right = NULL;
 
	return node;
}
 
TreeNode* CreatTree()
{
 
	TreeNode* node1 = BuyTreeNode(1);
 
	TreeNode* node2 = BuyTreeNode(2);
 
	TreeNode* node3 = BuyTreeNode(3);
 
	TreeNode* node4 = BuyTreeNode(4);
 
	TreeNode* node5 = BuyTreeNode(5);
 
	TreeNode* node6 = BuyTreeNode(6);
 
	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	//node2->right = NULL;
	//node3->left = NULL;
	//node3->right = NULL;
	node4->left = node5;
	node4->right = node6;
	//node5->left = NULL;
	//node5->right = NULL;
	//node6->left = NULL;
	//node6->right= NULL;
 
	return node1;
}
 
int main()
{
	TreeNode* root = CreatTree();
	return 0;
}

结点个数计算

错误方法

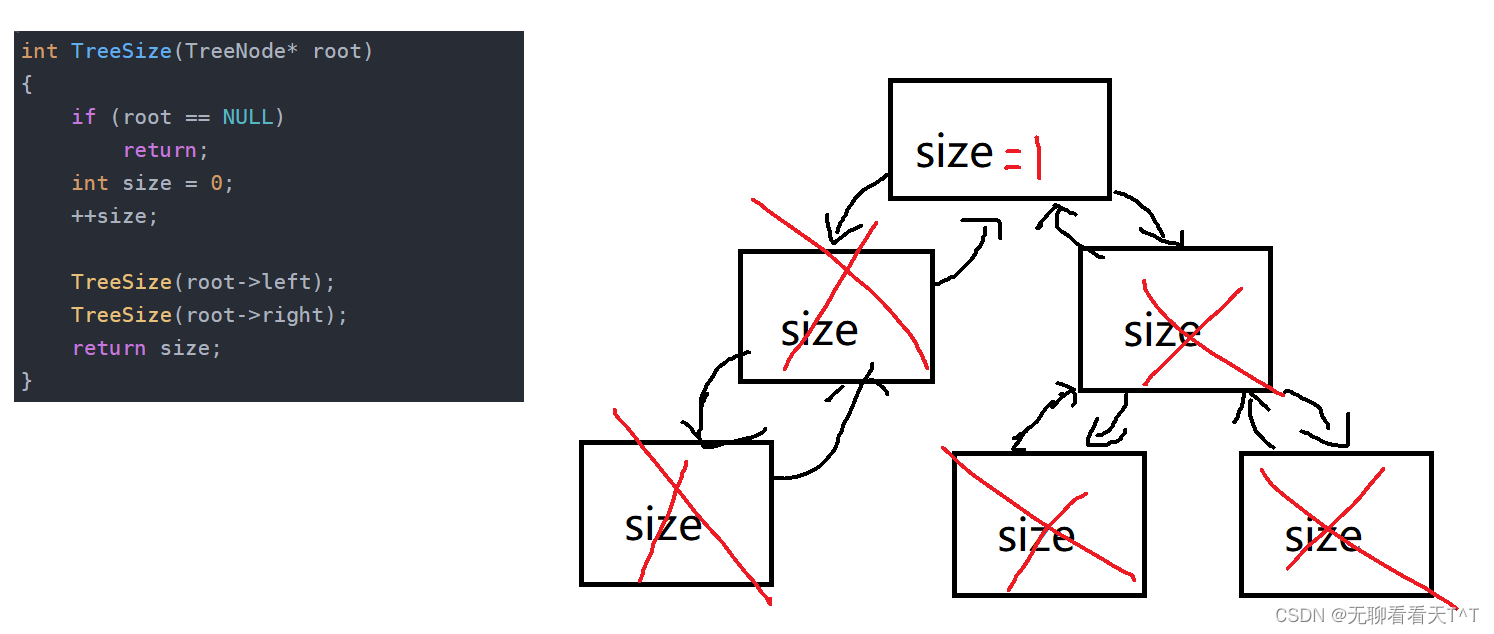
int TreeSize(TreeNode* root)
{
	if (root == NULL)
		return;
	int size = 0;
	++size;

	TreeSize(root->left);
	TreeSize(root->right);
	return size;
}

这是因为每一次的递归都会开辟出一个帧栈，而每一块的帧栈中都会有一个size且声明周期仅只在自己的帧栈范围内，在调用返回时所有的size并不会相加然后一起返回，简单来说就是生命周期有限

不便利方法

//二叉树代码
.....

static int size = 0;
int TreeSize(TreeNode* root)
{
	if (root == NULL)
		return;
	++size;

	TreeSize(root->left);
	TreeSize(root->right);

	return size;
}

int main()
{
	TreeNode* root = CreatTree();
	printf("TreeSize：%d\n", TreeSize(root));
	printf("TreeSize：%d\n", TreeSize(root));
	printf("TreeSize：%d\n", TreeSize(root));
	printf("TreeSize：%d\n", TreeSize(root));
	return 0;
}

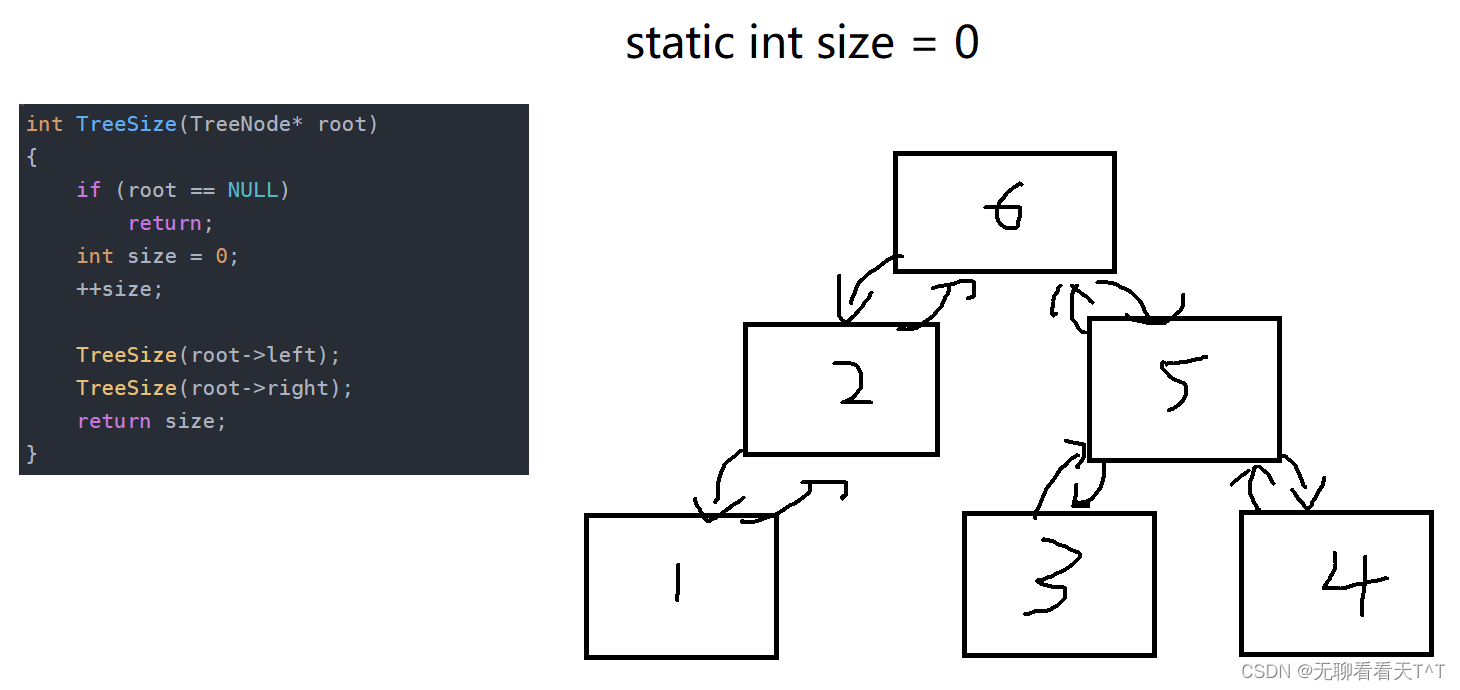
基于上次生命周期的问题，我们想到了用static来延长局部变量的生命周期，此时size的生命周期就是整个程序，但是当我们连续三次打印时发现三次的结果都不一样，每次都比上次的结果增加了6？这也是使用static的副作用，因为被static修饰的变量（静态变量）在整个程序中只会初始化一次，当第二次使用该静态变量时，此次的结果与上次的结果叠加，从而出现意料之外的问题

我们需要在首次打印后，后续的每次打印前将该静态变量人为置空后才能正常使用：

//二叉树代码
.....

static int size = 0;
int TreeSize(TreeNode* root)
{
	if (root == NULL)
		return;
	++size;

	TreeSize(root->left);
	TreeSize(root->right);

	return size;
}

int main()
{
	TreeNode* root = CreatTree();
	printf("TreeSize：%d\n", TreeSize(root));
    
    size = 0;
	printf("TreeSize：%d\n", TreeSize(root));

    size = 0;
	printf("TreeSize：%d\n", TreeSize(root));
    
    size = 0;
	printf("TreeSize：%d\n", TreeSize(root));
	return 0;
}

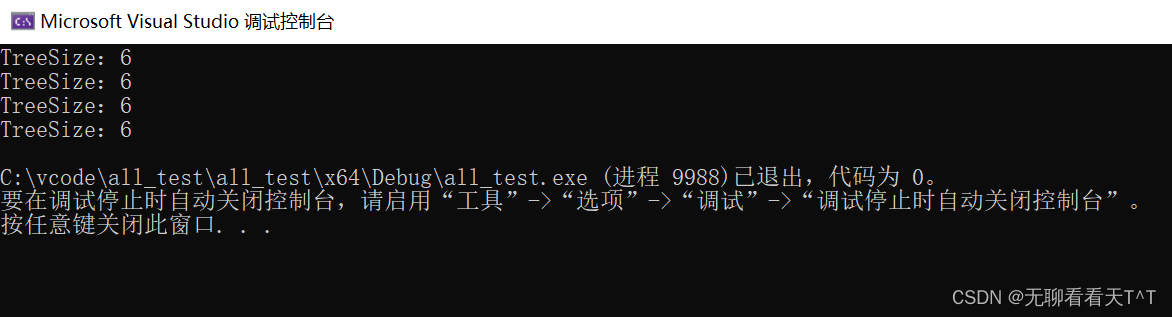
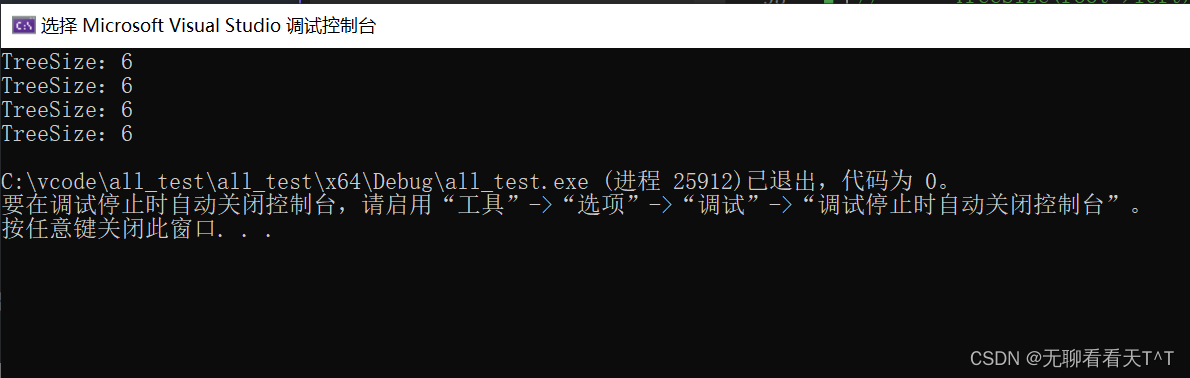
使用全局变量也是一样的效果，只需要对代码进行简单的更改即可：

//二叉树代码
.....

int size = 0;
void TreeSize(TreeNode* root)
{
	if (root == NULL)
		return;
	++size;

	TreeSize(root->left);
	TreeSize(root->right);
}


int main()
{
	TreeNode* root = CreatTree();
	TreeSize(root);
	printf("TreeSize：%d\n", size);

	size = 0;
	TreeSize(root);
	printf("TreeSize：%d\n", size);

	size = 0;
	TreeSize(root);
	printf("TreeSize：%d\n", size);

	size = 0;
	TreeSize(root);
	printf("TreeSize：%d\n", size);
	return 0;
}

基于分治思想的方法

//二叉树总结点个数
int TreeSize(TreeNode* root)
{
	return root == NULL ? 0 :
		TreeSize(root->left) +
		TreeSize(root->right) + 1;
}

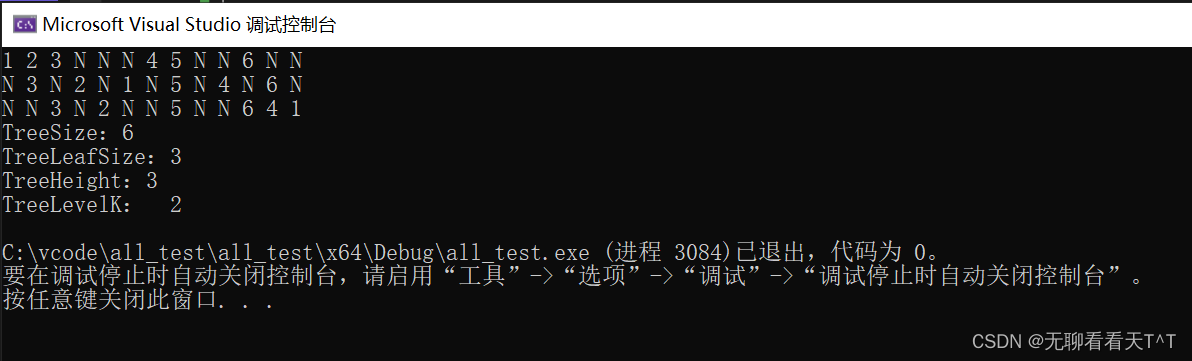
解释：主体逻辑就是判断此时所处结点的值是否为空，若不为空则进行左递归，左递归结束后进行右递归，每一次左右递归完全结束后就会返回一个1，每次返回的结果可以叠加

叶子结点个数

//叶子结点个数
int TreeLeafSize(TreeNode* root)
{
	//空树 返回0
	if (root == NULL)
		return 0;

	//非空树，但是没有左右子树（叶子结点/仅有一个结点的树）返回1
	if (root->left == NULL && root->right == NULL)
		return 1;

	//不是空 也不是叶子结点
	return TreeLeafSize(root->left) +
		TreeLeafSize(root->right);
}

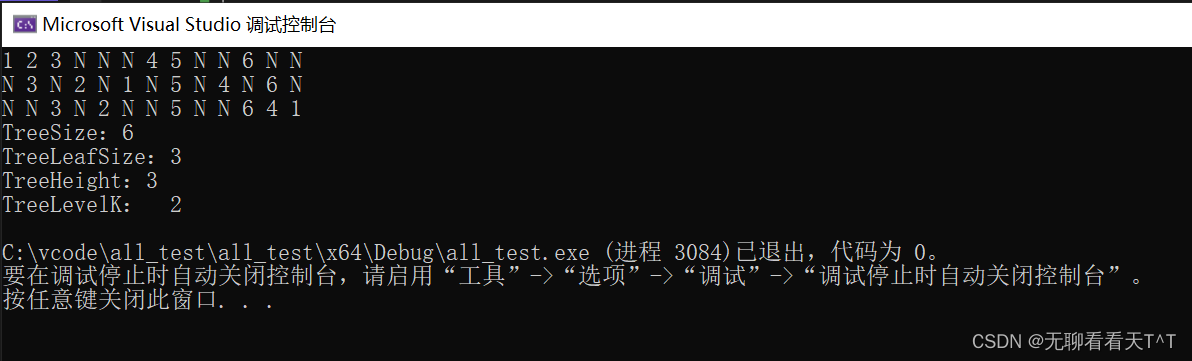
解释：主体逻辑与获取结点总数时没有区别，但是这里增加了一个用于判断叶子结点的判断条件，因为叶子结点的特殊性（没有左右子树），所以我们的返回1的操作操作必须要在确定该结点为叶子结点时才会返回

树的高度

//树的高度
int TreeHeight(TreeNode* root)
{
	if (root == NULL)
		return 0;
	int leftHeight = TreeHeight(root->left);
	int rightHeight = TreeHeight(root->right);

	return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

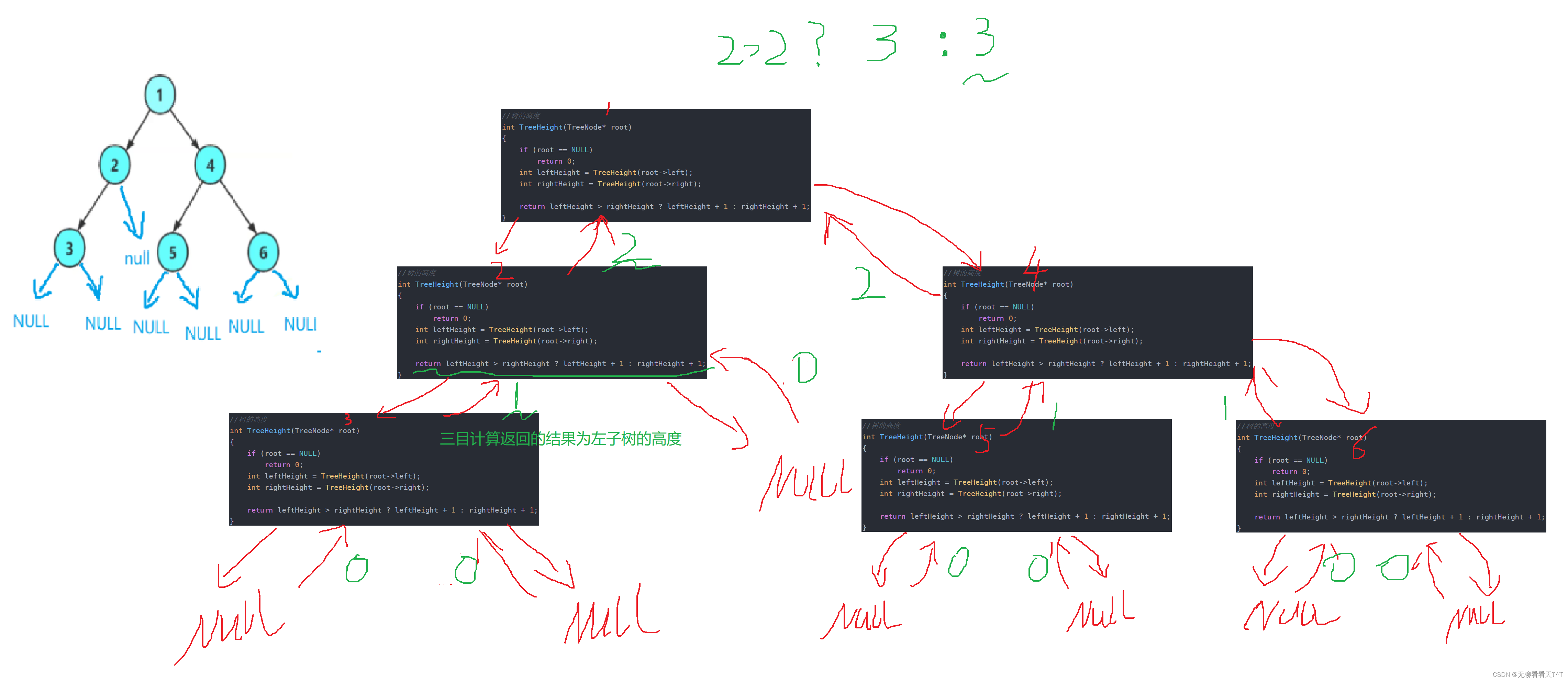
设计思想：

如果即当前子树为空，则返回 0，表示该子树没有任何结点，因此高度为 0
如果传入的 root 指针不为空，则执行以下操作：
a）调用递归函数 TreeHeight(root->left) 来计算左子树中结点到达最底层所需经过的边数，并将结果赋值给变量 leftHeight
b）调用递归函数 TreeHeight(root->right) 来计算右子树中结点到达最底层所需经过边数，并将结果赋值给变量 rightHeight
c）返回左右子树两者中较大者加上当前节点本身所代表边数（加1）作为该子问题下一级别解答（理解这里十分重要）

解释： 1、某个结点的左子树递归的三目运算符的运算结果都会在最后赋值给leftHeight，右子树递归的三目运算符的运算结果都会在最后赋值给rightHeight

2、每次调用 TreeHeight 函数时都会进行三目运算符的比较，如果是叶子结点，由于没有左右子树为空所以两次递归返回的值均为0，即leftHeight和rightHeight的值均为0（因为0>0为假，故：rightHeight+1，此时rightHeight+1里的+1是为了加上3结点本身的高度，不可能因为左右子树均为空就没有高度了，当前结点也算一个高度）比较后会返回1它被赋值给leftHeight，因为它是2结点的左子树递归得到的，同时它也告诉了2结点你的左子树高度只有1，然后2结点又会递归调用它的右子树但是由于右子树为NULL所以会返回0，所以此时leftHeight和rightHeight的值分别为1和0（因为1>0为真所以leftHeight+1，表明2结点的左子树大于右子树，左子树的高度可以代表2结点的高度）比较后会返回2它被赋值给leftHeight，因为它是1结点的左子树递归得到的，同时它也告诉了1结点你的左子树高度为2

3、然后1结点会递归它的右子树，剩余步骤与上面描述的大致相似，最后右递归会告诉1结点你的右子树高度为2（因为2>2为假所rightHeight+1，此时rightHeight+1里的+1是为了加上1结点本身的高度，不可能左右子树高度相等就没有高度了，当前结点也算一个高度，所以当前结点的左右子树结点高度相等，将当前左右结点子树的高度+1就是整个树的高度）

第k层结点的个数

//第k层结点的个数，k==2
int TreeLevelK(TreeNode* root,int k)
{
	assert(k > 0);
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;

	return TreeLevelK(root->left, k - 1) +
		TreeLevelK(root->right,k-1);
}

设计思想：

树为空，返回0
树不为空且是第一层结点个数，返回1
树不为空且是第n(n>1)层结点的个数，返回(左子树的k-1层 + 右子树的k-1层)

k-1而不是k，k相当于判断条件count，当count==1的时候就相当于找到了我们要找的那一层，如果为k，那么递归的返回条件就不存在

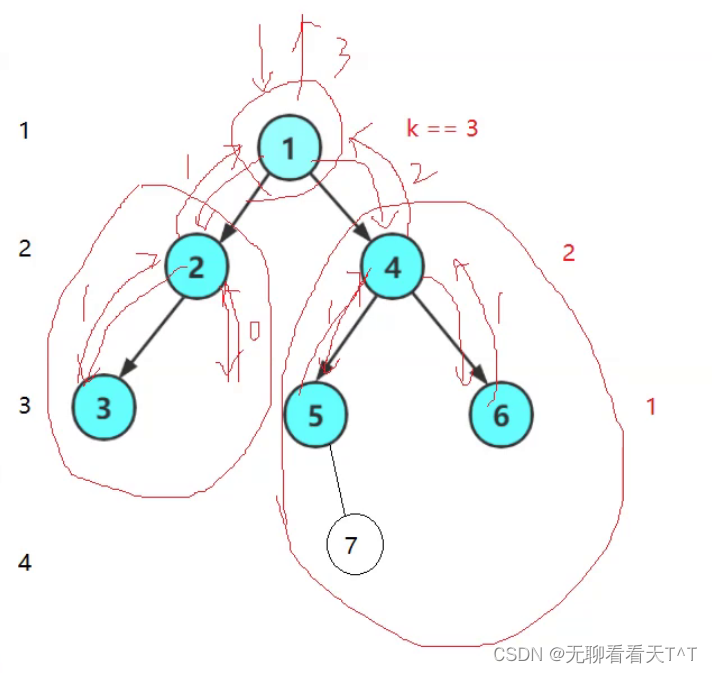
解释：

1、查找第3层结点个数，即k == 3

2、树不为空，并且k != 1，所以递归结点1的左子树，结点2不为空，此时k-1 = 2 != 1，所以可以继续递归结点2的左子树，结点3不为空，此时k-1 = 1 == 1，所以返回1，即递归结点2左子树的返回值为1，然后递归结点2的右子树，右子树为空返回0，最后0+1=1，即递归结点1左子树的返回值为1，这说明结点1左子树第3层的结点个数为1

3、然后递归结点1的右子树，结点4不为空，此时k-1 = 2 != 1，所以可以继续递归结点4的左子树，结点5不为空，此时k - 1 =1 == 1，所以返回1，即递归结点4的左子树的返回值为1，然后递归结点4的右子树，结点6不为空，此时k - 1 =1 == 1（这是因为此时处于结点4的TreeLevelK函数中，此时的k为2），所以返回1，即递归结点4的右子树的返回值为1，最后1+1=2，即递归结点1右子树的返回值为2，这说明结点1右子树第3层的结点个数为2

4、最后结点1的左右子树均递归完璧，1+2=3，即该二叉树第3层的结点个数为3

~over~