文章目录
一、直接插入排序
思想
程序代码
时间复杂度
二、希尔排序
思想
程序代码
时间复杂度
三、冒泡排序
思想
程序代码
时间复杂度
四、选择排序
思想
程序代码
时间复杂度
一、直接插入排序
思想
直接插入排序有些类似于我们玩扑克牌时的整理牌序动作,比如有整理好的手牌是 3,3,3,4,6,7,8,9,10,J,J,K;还差一张手牌 5 没有整理好,那么一般而言是会把 5 放在 4 的后面。而直接插入排序也类似,在一个有序序列中插入若干个数字,使最后的序列也是有序的。可以使用下图的做法:
这里可能会比较疑惑,为什么不从左边开始比较,而从右边开始比较?一方面,从左或者从右比较两者没有什么差别,只是在上图的具体例子中,从左边插入确实比较的次数要少一些。另一方面,如果从左边插入,就只能找到 “3” 该在的位置,然后一次将后面的数据全部移走,这样子写代码比较麻烦,不如比较一次,移动一个数据。
那么如果给一个乱序的序列,如何将其排好序呢?比如[ 5,1,6,2,9,4,5,7,10 ] ,其实也是类似的原理,只需要把第一个数据看作是有序的(因为它本来就只有一个数据),然后将第二个数据按上面的算法插入进去,这样前两个数据就有序。然后将第三个数据插入……直到最后,所有数据就都有序了。
程序代码
如下,只需要套一层循环,用 i 来控制,将第1个数据看作是有序的,从第二个数据开始插入,每一次插入一个数据。因为有 n 个数据,所以下标最多是n-1 。
void InsertSort(int* p, int n)
{
for (int i = 0;i < n - 1;i++)
{
int end = i;
int temp = p[i + 1];
while (end >= 0)
{
if (p[end] > temp)
{
p[end + 1] = p[end];
end--;
}
else
break;
}
p[end + 1] = temp;//这一句不能写在else里面,是因为如果end=-1,那么不会进入while循环,也就白比较和后移了
}
}时间复杂度
直接插入排序的时间复杂度还是很好分析的,按最坏的情况来看,一轮排序中,每次都要和所有数据比较完才停下来。比如有[ 3,4,5,6,8] ,然后本次要插入的是数据 "2" ,需要比较到从右往左最后一个数据 “3” ,才发现也不满足,此时由于end 小于0,才跳出循环。
这样子导致每次都要比较 i 次,所以时间复杂度= 1+2+3+……+ N = (N*N+N)/ 2,所以时间复杂度为O(N^2)。
二、希尔排序
上面说到,直接插入排序可能会面临最坏的情况,就是原本升序的数据,要排成降序,这样每一个数据都要移动最多次。为了优化这个问题,D.L.Shell 于1959年发明了希尔排序。
思想
此排序算法主要是将无序数组分割为若干个子序列,子序列不是逐段分割的,而是相隔特定的增量(记为gap)的子序列,对各个子序列进行插入排序;然后再选择一个更小的增量,再将数组分割为多个子序列进行排序......最后选择增量为1,即使用直接插入排序,使最终数组成为有序。
如下图,假设此时 gap 为3,也就是下标间隔为3的数据是一个子序列。当进行第一组排序时,如图红色数据就是第一组,使用直接插入排序的算法。进行第二组排序时,第一组的数据已经排好了,下图也可以看出,然后进行蓝色的第二组数据排序。进行第三组排序时,前两组都排好了,进行绿色的第三组数据排序,得到最后的结果。
最后得出的数据,虽然不是一个有序序列,但是相较之前的数据,已经相对有序了:值大的已经相对而言移到后面了,小的相对而言移到前面,这样子最后使用直接插入算法升序排序的时候,就会大大减少出现最坏的情况。
然后再对该组数据,进行 gap=1 的同样操作,gap=1就是直接插入排序,此时的数据相较于之前的数据,已经好排序多了,数据要移动的次数大大减少,时间复杂度得到了优化。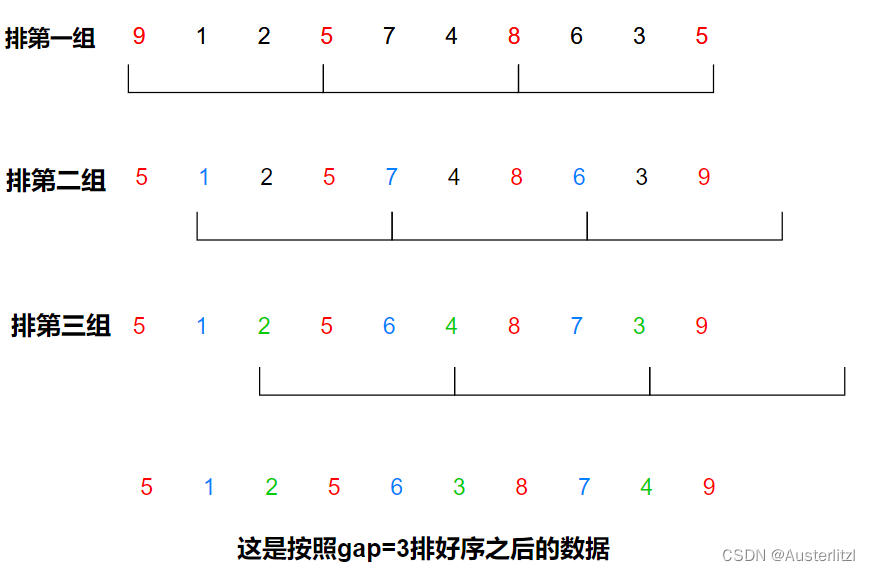
但是此时,我们能不能把这个方法优化一下呢?这样一组一组比过去是否过于麻烦?我们可以化整为零,将一组一组分散成一对一对。如下图,gap也是3,9和5,1和7,2和4,分别是上面三组的第一次比较内容,这里我们按顺序第一次、第二次、第三次分别排序这三对数据,而不是之前一组一组来。
三次完成之后,到了第四次,即原本第一组数据的第二对数据 9和8 ,在之前的方法里,这对数据应该是第二次就排序了,但是在这里是第四次。
再后面的某一次,也会到原本第一组数据的最后一对,如下图第三行(这里不仔细画出其中间排序的结果)。这样就将原本集中排序的第一组数据,分散为多次排序,每次排一对数据。另外两组也是同理。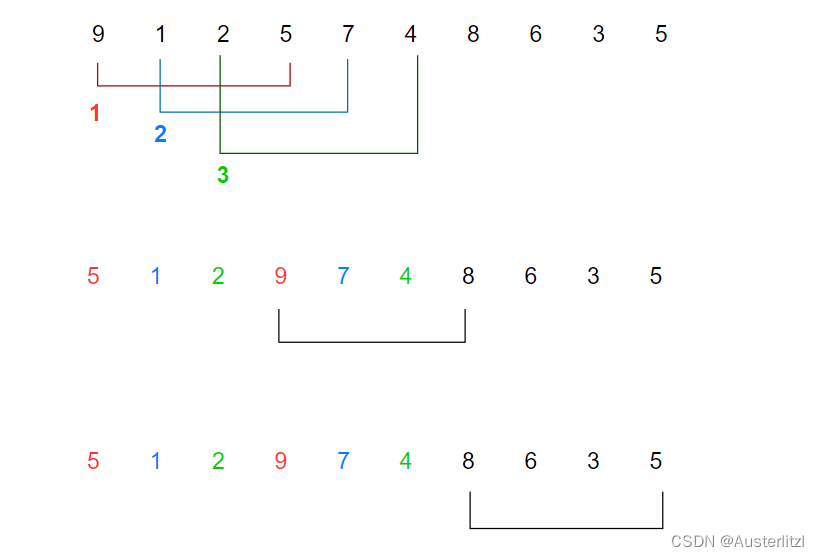
优化后的排序算法,其代码如下,可以对比上文的直接插入排序算法进行更好的理解,其实就是原本的gap=1,变成了gap=3 :
gap = 3;
for (int i = 0;i < n - gap;i++)
{
int end = i;
int temp = p[i + gap];
while (end >= 0)
{
if (p[end] > temp)
{
p[end + gap] = p[end];
end -= gap;
}
else
break;
}
p[end + gap] = temp;程序代码
代码如下,gap是自己设置的,数据多的时候,可能一开始是一个比较大的数字,比如15,并不是gap=15 排完之后就立刻排 gap =1 的情况,要逐层来,比较好的方法就是 gap/=2。第一次gap=15,第二次gap=7,第三次为3,第四次为1,这样子第四次排完之后,就完成排序了。控制条件就是在最外面加一个while循环,gap=1 的情况排完序之后,就跳出循环了。
void ShellSort(int *p,int n)
{
int gap=n;
while (gap > 1)
{
gap /= 2;//这样的好处是gap最后可以得到1
for (int i = 0;i < n - gap;i++)
{
int end = i;
int temp = p[i + gap];
while (end >= 0)
{
if (p[end] > temp)
{
p[end + gap] = p[end];
end -= gap;
}
else
break;
}
p[end + gap] = temp;
}
}
}时间复杂度
希尔排序时间复杂度约为O(N^1.3),这个推导过程属实比较繁琐(其实是目前还未掌握..),所以就先不写啦!!
三、冒泡排序
思想
冒泡排序重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。
假设有N个数据,需要升序排序,那么就要冒泡N-1次,每一次都把当前序列的最大值放到最后的位置,最后剩下的那个数据不需要冒泡,因为它就是最小的。示意图如下:
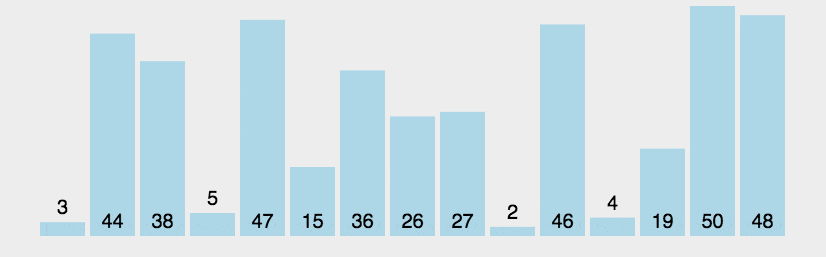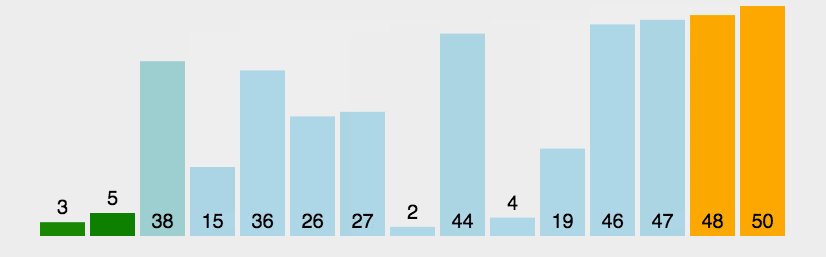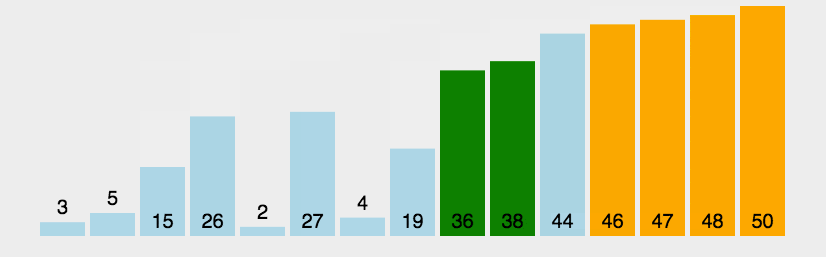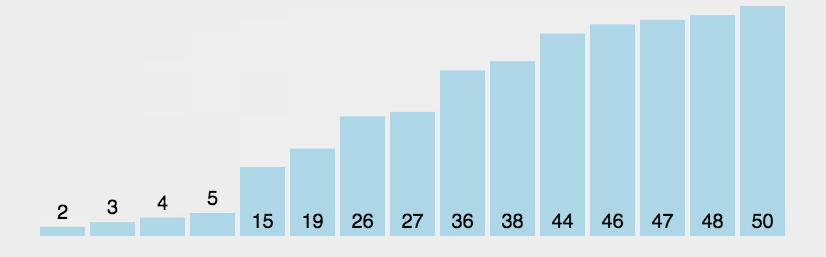
程序代码
void BubbleSort(int* p, int n)
{
for (int i = 0;i < n - 1;i++)//冒泡次数,假设有4个数据,实际上冒泡好三个数据,剩下的就是最小的
{
int exchange = 0; // 标记一下,如果本轮冒泡没有数据交换,就是排好序了,退出循环
for (int j = 0;j < n - i - 1;j++) //看第一次冒泡,假设有4个数据,那么只需要到第三个即可,因为下面的逻辑是当前数据和下一个数据比较
{
if (p[j] > p[j + 1])
{
Swap(&p[j], &p[j + 1]);
exchange = 1;
}
}
if (exchange == 0)
return;
}
return;
}时间复杂度
假设有N个数据,需要冒泡N-1次,如果每次冒泡都是最坏的情况,需要交换数据的次数都是拉满,那么总共需要交换数据的次数是: (N-1) + (N-2) + (N-3) + (N-4) + …… + 1 。最后算出来的结果是:N*(N-1) / 2 ,所以时间复杂度为 O(N^2)。
四、选择排序
思想
选择排序是一种简单直观的排序算法,无论什么数据进去都是 O(n²) 的时间复杂度。所以用到它的时候,数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。
思想是,首先在未排序序列中找到最小(大)元素,分别存放到序列的起始位置。再从剩余未排序元素中继续寻找最小(大)元素,然后放到未排序序列的起始位置。重复第二步,直到所有元素均排序完毕。
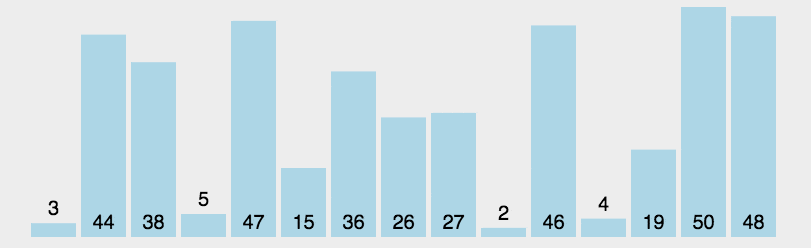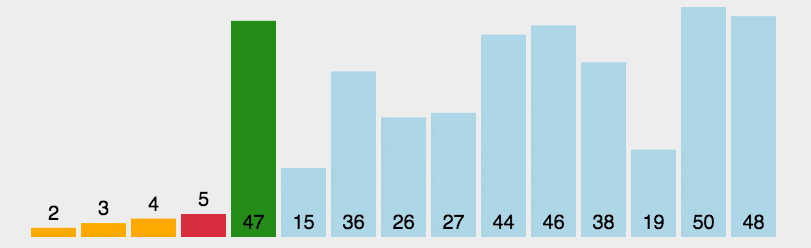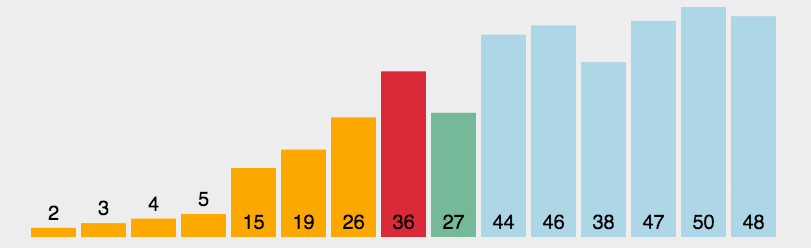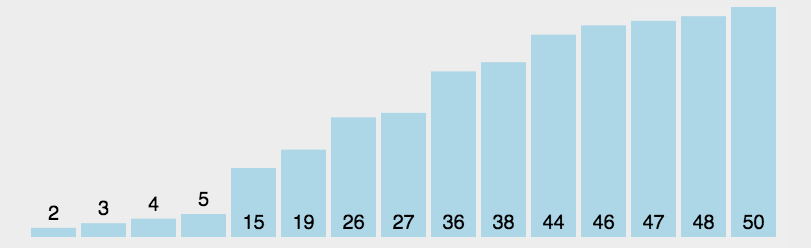
但是,可不可以优化一下子算法呢?一次找两个如何?在未排序序列中,寻找到最大的和最小的数据,记下来,然后最小的和当前序列起始位置互换,最大的和当前序列末尾位置互换。重复此过程,最后得到的也是一个升序序列。
如下图,第一次交换最大和最小的两个数据之后,首位两端算是排好了,第二次就要对中间未排的数据进行排序,重复此过程直到排完。
但是,由于是要交换两个数据,难免会出现如下状况,避免错误的机制就是,交换完最小的数据和当前序列首位的数据之后,改变记录最大的数据下标的变量,让它变成正确的。具体可见下面的代码。
程序代码
如下代码:
void SelectSort(int* a, int n)
{
int begin = 0, end = n - 1;
while (begin < end)
{
int mini = begin, maxi = begin;
for (int i = begin + 1; i <= end; ++i)
{
if (a[i] < a[mini])
{
mini = i;
}
if (a[i] > a[maxi])
{
maxi = i;
}
}
Swap(&a[begin], &a[mini]);
if (maxi == begin)
maxi = mini;
Swap(&a[end], &a[maxi]);
++begin;
--end;
}
}时间复杂度
任何情况都是O(N^2) 包括有序或接近有序。因为要一个一个比过去的。