CG相机模型
在图形学中最常用的相机模型的原理和小孔成像是类似的。
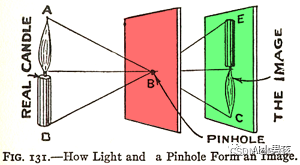
不同之处在于,如上图,小孔成像得到的图像是倒立的,但是我们希望得到的图像是正向的,因此,我们选择小孔前成像。
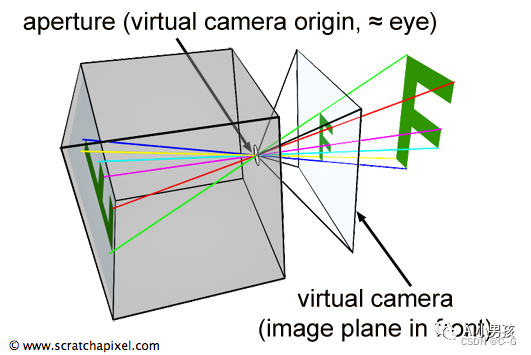
从 3D 到 2D 的投影,就是根据 3D 物体的坐标,计算其投影到 2D 成像平面上的坐标。对于一个已有的相机而言,只有在恰当位置范围内的 3D 物体才可能投影到成像平面上。这个恰当范围,跟成像平面的大小,以及相机中心到平面距离等因素有关。
在图形学中有一个专门的模型来定义这个范围:
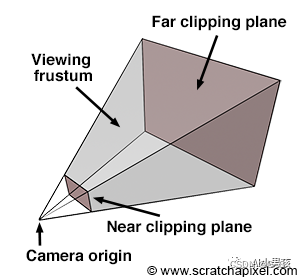
上图这个形似棱锥的模型,就是相机的可视范围。其中,有两个重要的概念:Near clipping plane 和 Far clipping plane。
Near clipping plane 是相机前方的平面,也就是成像平面,Far clipping plane 是更远处的平面,限制了相机最远可视的范围,它们都与相机的 z 轴垂直。在这两个平面之间的空间,就是相机的可视范围。在这个范围内的物体,才能投影到相机的成像平面上。在图形学中,这个可视范围被称为视锥体 (Viewing Frustum)。
在真实的相机中,Far clipping plane 一般是无限远的,但在图形学中,为了简化计算,一般将其设置为有限的距离。
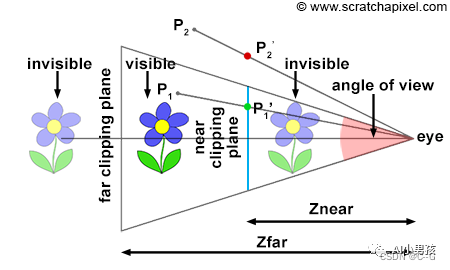
3D坐标到2D坐标

上图是一个典型的物体投影到屏幕上的过程。我们假设已经获得了物体在世界坐标系中的坐标,在世界坐标系转换到图像坐标系的过程中,涉及以下过程。
世界坐标系转换到相机坐标系
对三维物体投影的第一步,是将三维物体从世界坐标系转换到以相机为中心的坐标系统,这样方便后续的投影计算。
相机坐标系是以相机为中心的坐标系 (也叫 eye coordinates),由于相机和世界坐标系的原点可能不同,且其坐标轴方向和世界坐标系可能不同,因此世界坐标系和相机坐标系的转换一般涉及旋转平移两项操作。
在图形学中,通常使用齐次坐标,并配合 4x4 的矩阵来完成两个坐标系统的转换。
相机坐标系到屏幕坐标系
获得物体的相机坐标系(Near clipping plane 和 Far clipping plane 之间)后,接下来就可以计算物体投影到成像平面上的坐标。
这个过程可以根据相似三角形的原理计算得出。
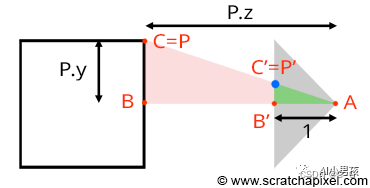
如上图所示,假设相机的中心在 A 点,三维物体在 C 点,其在成像平面上的投影为 C’。
由于我们已经获得了物体在相机坐标系中的坐标,因此可以计算出 AB、BC 的长度。而 AB’、B’C’ 的长度,可以根据相似三角形的原理计算出来 (上图假设相机焦距是 1,但实际情况中不做限制,我们用 Z n e a r Z_{near} Znear表示):
B C A B = B ′ C ′ A B ′ \frac{BC}{AB} = \frac{B'C'}{AB'} ABBC=AB′B′C′
即
P . y ∣ P . z ∣ = P ′ . y Z n e a r P ′ . y = Z n e a r ∗ P . y ∣ P . z ∣ \frac{P.y}{|P.z|} = \frac{P'.y}{Z_{near}} \\ P'.y = \frac{Z_{near}*P.y}{|P.z|} ∣P.z∣P.y=ZnearP′.yP′.y=∣P.z∣Znear∗P.y
同样的,可以算出 : P ′ . x = Z n e a r ∗ P . x ∣ P . z ∣ P'.x = \frac{Z_{near}*P.x}{|P.z|} P′.x=∣P.z∣Znear∗P.x
对于 z 轴坐标来说,由于 Near clipping plane 和 z 轴是垂直的,因此所有投影到成像平面上的点,z 坐标都是相同的。而事实上在投影到 2D 坐标后,z 轴坐标已经没有意义了,因此可以直接忽略。
从 P ′ . x P'.x P′.x 和 P ′ . y P'.y P′.y 可以发现,投影到成像平面上的坐标,其 x 和 y 坐标都是除以 z 坐标得到的。因此这种投影变换也被称为 z divide 或者 perspective divide。这也是透视投影的特点,投影到成像平面上的坐标,其 x 和 y 坐标都是 与 z 坐标绝对值成反比的。也因此,物体越远,其在屏幕上的大小越小。
屏幕坐标系到图像坐标系
转换到屏幕坐标系后,我们理论上已经获得了物体的 2D 坐标,但这个坐标并不是最终图像上的坐标。
在第 2 步相机坐标系到屏幕坐标系的转换中,不难发现,屏幕坐标系的原点是在屏幕中心的,但在图像坐标系中,原点一般是在左上角或者左下角。因此,要转换到图像坐标系,还需要一步归一化的过程。
在不同的系统中,图像坐标系的原点是存在差异的。比如,有些系统中的图像原点位于左下角,y 轴朝上,但有些则反着来。而 NDC 坐标系是一个跟设备无关的坐标系统,它将图像的 x/y/z 轴都统一归一化到 [0, 1],并规定了坐标轴方向 (在有些图形系统中,也会将 x/y/z 轴归一化到 [-1, 1]),如下图所示 (中间即是 NDC 坐标系)。
NDC 全称是 Normalized Device Coordinate,也即归一化的设备坐标系。这是从屏幕坐标系转换到图像坐标系的中间媒介。
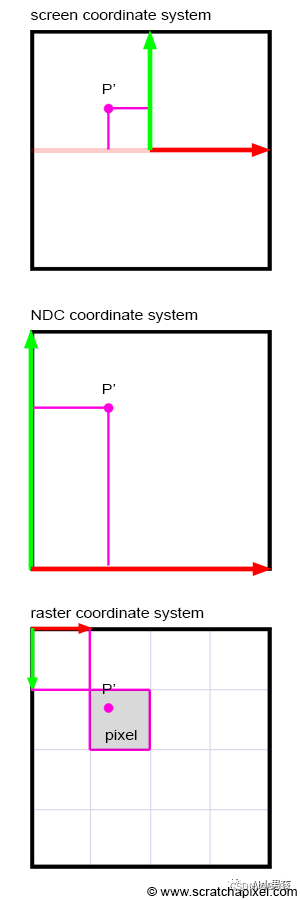
用上图的例子来演示 屏幕坐标系 -> NDC 坐标系 -> 图像坐标系 (即上图的 raster 坐标系) 的转换过程。
假设 投影屏幕 长宽分别为 height、width,NDC 的原点在左下角,y 轴朝上,那么,屏幕坐标系到 NDC 坐标系的转换公式为:
P b d c . x = P ′ . x + w i d t h / 2 w i d t h P b d c . y = P ′ . y + h e i g h t / 2 h e i g h t P_{bdc}.x = \frac{P'.x+width/2}{width} \\ P_{bdc}.y = \frac{P'.y+height/2}{height} Pbdc.x=widthP′.x+width/2Pbdc.y=heightP′.y+height/2
假设图像大小为 image_height、image_width,图像原点位于左上角,y 轴朝下。那么,NDC 坐标系到图像坐标系的转换公式为:
P i m a g e . x = P n d c . x ∗ i m a g e _ w i d t h P i m a g e . y = ( 1 − P n d c . y ) ∗ i m a g e _ h e i g h t P_{image}.x = P_{ndc}.x * image\_width \\ P_{image}.y = (1-P_{ndc}.y) * image\_height Pimage.x=Pndc.x∗image_widthPimage.y=(1−Pndc.y)∗image_height
NDC 坐标系是连续的坐标系,只有转换到图像坐标系,才会对坐标进行取整操作。此外,NDC 坐标系仍是三维坐标系,不过在考虑投影的时候,z 轴通常会被忽略
OpenGL 中,NDC 坐标到 raster 图像坐标的转换过程,也被称为 viewport transform
采用 NDC 坐标的好处是,我们可以将 NDC 看作是一个通用的坐标系统,并将不同系统的坐标统一起来。比如,我们在将屏幕坐标系转换到图像坐标系时,可以先换算到统一的 NDC 坐标系中,再实现二者的相互转化。在 NDC 坐标系中进行处理的时候,就不需要关心投影屏幕长宽、图像大小等信息了。
投影矩阵(Projection Matrix)
从上面三维坐标到二维坐标的转换过程中,不难发现,整个过程涉及步骤很多,非常繁琐。为了简化计算,在很多图形系统中,会将物体从相机坐标系到 NDC 坐标系的过程,用一个矩阵串联起来 (即投影矩阵)。
即完成所有操作总共需要两个矩阵:世界坐标系和相机坐标系之间的变换矩阵、投影矩阵。
理解投影矩阵,对后面 NeRF 中 NDC 坐标系统的推导至关重要。因此,这里先详细介绍投影矩阵的由来,并补充一些相关的数学知识。
不同坐标系统的转换
三维坐标转二维坐标的第一步,就是将物体从世界坐标系转换到相机坐标系。
这一步在投影矩阵的求解中是不需要的。不过,由于图形学中,不同坐标系之间的转换是一个基本操作。
任何三维坐标系统,都可以用三个互相垂直的坐标轴以及坐标原点来唯一确定。
这三个坐标轴,在线性代数中,也被称为基向量v={ v 1 , v 2 , v 3 v_1,v_2,v_3 v1,v2,v3} 。通常情况下,我们会用标准向量 e 1 = [ 1 , 0 , 0 ] e_1=[1,0,0] e1=[1,0,0]、 e 1 = [ 0 , 1 , 0 ] e_1=[0,1,0] e1=[0,1,0]、 e 1 = [ 0 , 0 , 1 ] e_1=[0,0,1] e1=[0,0,1] 来表示这三个坐标轴。不过事实上也可以随意定义,只要它们线性无关,可以表达出整个三维空间即可。
现在,假设有两个不同的坐标系统 A 和 B。A 的基向量 v = { v 1 , v 2 , v 3 } v=\{v_1,v_2,v_3\} v={v1,v2,v3},B 的基向量 u = { u 1 , u 2 , u 3 } u=\{u_1,u_2,u_3\} u={u1,u2,u3} 。根据线性无关,可以得出:
u 1 = γ 11 v 1 + γ 12 + γ 13 v 3 u 2 = γ 21 v 1 + γ 22 + γ 23 v 3 u 3 = γ 31 v 1 + γ 32 + γ 33 v 3 u_1 = \gamma_{11}v_1+\gamma_{12}+\gamma_{13}v_3 \\ u_2 = \gamma_{21}v_1+\gamma_{22}+\gamma_{23}v_3 \\ u_3 = \gamma_{31}v_1+\gamma_{32}+\gamma_{33}v_3 \\ u1=γ11v1+γ12+γ13v3u2=γ21v1+γ22+γ23v3u3=γ31v1+γ32+γ33v3
用矩阵方程的形式表示为:
u
=
M
v
u=Mv
u=Mv
对于三维空间中的某个点 w 来说,均可以由 u、v 这两个坐标系表示:
w
=
a
T
v
=
b
T
u
w=a^Tv=b^Tu
w=aTv=bTu
其中的 a T a^T aT和 b T b^T bT 其实就是 w 在这两个坐标系统中的坐标。再结合公式 (2),可以得到:
w = b T u = b T M v = a T v w=b^Tu=b^TMv=a^Tv w=bTu=bTMv=aTv
由此推出, a = M T b , b = ( M T ) − 1 a a=M^Tb,b=(M^T)^{-1}a a=MTb,b=(MT)−1a
到这里,我们就发现:对于点 w 来说,想要从坐标系 A 转换到坐标系 B,只需要对原坐标系 A 中的坐标,乘以一个矩阵 M 即可。反之,则是乘以矩阵的逆 ( M T ) − 1 (M^T)^{-1} (MT)−1。而这个矩阵M ,可以通过两个坐标系统的基向量,也就是坐标轴,通过公式 (1) 的矩阵方程进行求解。
在将物体从世界坐标系转到相机坐标系的过程中,只需要将这个矩阵应用到世界坐标系的物体坐标上,就可以得到三维物体相对于相机坐标系的位置坐标。
这个过程中,物体的实际位置没有发生任何改变,只不过它的坐标,从相对于世界坐标系,变成相对于相机坐标系。
齐次坐标(Homogenous Coordinates)
上面提到的变换矩阵 M 存在一点不足,那就是它只能表达旋转和缩放操作,但无法表达平移。具体原因有很多资料已做了描述,这里不再赘述。
在三维世界中,旋转、缩放、平移是三个最基础的操作,因此,为了将平移也融入矩阵运算中,人们引入了齐次坐标。
齐次坐标相比普通的三维坐标,就是在 x、y、z 之外,再引入一维 w:[x,y,z,w]。
同时我们规定 [x,y,z]=[x,y,z,w=1],即当 w=1 时,齐次坐标可以等价于普通的三维坐标。
如果 w ≠ 1 w\neq1 w=1 ,那换算方法是: [ x , y , z , w ] = [ x w , y w , z w ] [x,y,z,w] = [ \frac{x}{w},\frac{y}{w},\frac{z}{w}] [x,y,z,w]=[wx,wy,wz]。
引入齐次坐标后,变换矩阵自然也可以拓展成 4x4 的维度。
[ m 00 m 01 m 02 T x m 10 m 11 m 12 T y m 20 m 21 m 22 T z 0 0 0 1 ] ∗ [ x y z w = 1 ] \left[ \begin{matrix} m_{00} & m_{01} & m_{02} & T_x \\ m_{10} & m_{11} & m_{12} & T_y \\ m_{20} & m_{21} & m_{22} & T_z \\ 0 & 0 & 0 & 1 \end{matrix} \right] * \left[ \begin{matrix} x \\ y \\ z \\ w=1 \end{matrix} \right] m00m10m200m01m11m210m02m12m220TxTyTz1 ∗ xyzw=1
在 w=1 的情况下,矩阵第 4 列代表的,就是 x、y、z 对应的平移量。
在之后投影矩阵的计算过程中,齐次坐标的作用会更加明显。
投影矩阵推导
假设我们已经获得了物体在相机坐标系中的坐标 P e = [ x e , y e , z e ] P_e=[x_e,y_e,z_e] Pe=[xe,ye,ze] (如果只有世界坐标系,也可以通过前面所讲的不同坐标系统的变换,来转换到相机坐标系,这一步也属于相机外参标定的流程)。
将
P
e
P_e
Pe 从相机坐标系转换到 NDC 的过程,其实就是将
P
e
P_e
Pe 从下图左边的棱锥转换到右边的立方体的过程 (这里使用 OpenGL 中的坐标习惯,NDC 将 x/y/z 轴都归一化到 [-1, 1]):
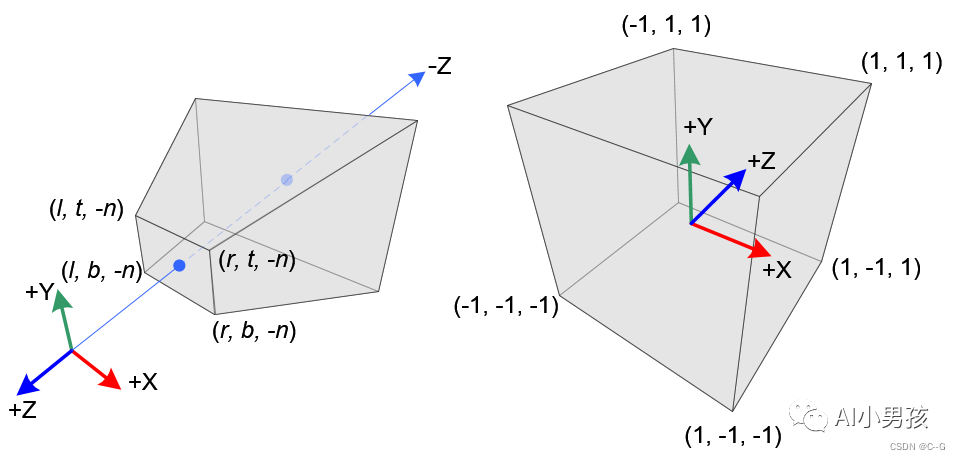
假设 Near Clipping Plane 到相机中心的距离为 n。在 OpenGL 等图形库中,由于相机坐标系的 z 轴是朝向屏幕外的,因此 Near Clipping Plane 上,点的 z 坐标均为 z = -n。
再假设 Near Clipping Plane 平面上,x 轴的屏幕范围是 [l,r],y 轴的屏幕范围是 [b,t],那么屏幕上四个边界点的坐标分别是:(l,t,-n)、(r,t,-n)、(l,b,-n)、(r,b,-n)
首先,将点 P e P_e Pe 投影到 Near Clipping Plane 上。根据上文的介绍,这就是 z divide 的过程,由此得到投影后的坐标为:
x p = n ∗ x e − z e y p = n ∗ y e − z e x_p = \frac{n*x_e}{-z_e} \\ y_p = \frac{n*y_e}{-z_e} \\ xp=−zen∗xeyp=−zen∗ye
在投影后需要考虑把超出屏幕的点裁剪掉,不过这一步也可以放在后面进行,我们先跳过。
接下来就是把投影后的点转换到 NDC 空间了,这是归一化的过程,把 [l,r] 和 [b,t] 这两个区间的数值归一化到 [-1,1] 。可以分两步完成。
先把 x p x_p xp 归一化到 [0,1]: x p − l r − l \frac{x_p-l}{r-l} r−lxp−l。
再从 [0,1] 归一化到 [-1,1]: 2 ∗ x p − l r − l − 1 2*\frac{x_p-l}{r-l}-1 2∗r−lxp−l−1。
x n d c = 2 ∗ x p − l r − l − 1 = 2 x p r − l − r + l r − l x_{ndc} = 2 * \frac{x_p-l}{r-l}-1 \\ = \frac{2x_p}{r-l} - \frac{r+l}{r-l} xndc=2∗r−lxp−l−1=r−l2xp−r−lr+l
同理可得
y
n
d
c
y_{ndc}
yndc:
y
n
d
c
=
2
y
p
t
−
b
−
t
+
b
t
−
b
y_{ndc} = \frac{2y_p}{t-b} - \frac{t+b}{t-b}
yndc=t−b2yp−t−bt+b
由此我们已经得到了 NDC 中的 x/y 坐标(将上述 y p , x p y_p,x_p yp,xp代入)。完整的转换公式:
x n d c = 2 n ∗ x e − z e ∗ ( r − l ) − r + l r − l y n d c = 2 n ∗ y e − z e ∗ ( t − b ) − t + b t − b x_{ndc} = \frac{2n*x_e}{-z_e*(r-l)} - \frac{r+l}{r-l} \\ y_{ndc} = \frac{2n*y_e}{-z_e*(t-b)} - \frac{t+b}{t-b} xndc=−ze∗(r−l)2n∗xe−r−lr+lyndc=−ze∗(t−b)2n∗ye−t−bt+b
这个公式看起来复杂,但可以融入到齐次坐标中,变成矩阵运算:
[ x c y c z c w c ] = [ 2 n r − l 0 r + l r − l 0 0 2 n t − b t + b t − b 0 0 0 A B 0 0 − 1 0 ] ∗ [ x e y e z e w e = 1 ] \left[ \begin{matrix} x_c \\ y_c \\ z_c \\ w_c \end{matrix} \right ] = \left[ \begin{matrix} \frac{2n}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\ 0& \frac{2n}{t-b} & \frac{t+b}{t-b} & 0 \\ 0& 0 & A & B \\ 0& 0 & -1 & 0 \\ \end{matrix} \right] * \left[ \begin{matrix} x_e \\ y_e \\ z_e \\ w_e = 1 \end{matrix} \right] xcyczcwc = r−l2n0000t−b2n00r−lr+lt−bt+bA−100B0 ∗ xeyezewe=1
其中 A、B是待求解的参数。
以
x
c
x_c
xc 为例,计算过程如下:
x
c
=
2
n
x
e
r
−
l
+
r
+
l
r
−
l
∗
z
e
w
c
=
−
z
e
x_c = \frac{2nx_e}{r-l} + \frac{r+l}{r-l} * z_e \\ w_c = -z_e
xc=r−l2nxe+r−lr+l∗zewc=−ze
由于 w ≠ 1 w\neq1 w=1,需要除去 w 才能得到最终的坐标
x n d c = x c w c = 2 n ∗ x e − z e ∗ ( r − l ) − r + l r − l x_{ndc} = \frac{x_c}{w_c} \\ = \frac{2n*x_e}{-z_e*(r-l)} - \frac{r+l}{r-l} xndc=wcxc=−ze∗(r−l)2n∗xe−r−lr+l
这样子求出的 x n d c x_{ndc} xndc 和上述的一致,这就是使用齐次坐标的好处。
由于 r 和 l 是沿中心对称的,即 l=-r,所以 r-l=2r,r+l=0。同理 t-b=2t,t+b=0 。所以矩阵可以简化为:
[
n
r
0
0
0
0
n
t
0
0
0
0
A
B
0
0
−
1
0
]
\left[ \begin{matrix} \frac{n}{r} & 0 & 0 & 0 \\ 0 & \frac{n}{t} & 0 & 0 \\ 0 & 0 & A & B \\ 0 & 0 & -1 & 0 \end{matrix} \right]
rn0000tn0000A−100B0
上面的矩阵中,还缺失 z e z_e ze 对应的参数 A、B。由于 z 轴的计算和 x/y 无关,因此矩阵第三行 x/y 对应的参数可以直接设为 0,我们单独看A、B 如何求解。
由上面的矩阵可以算出: z n d c = A ∗ z e + B − z e z_{ndc} = \frac{A*z_e+B}{-z_e} zndc=−zeA∗ze+B
假设 Far Clipping Plane 到相机中心的距离为 f 。那么 z 轴是从 [-n,-f] 归一化到 [-1,1],即 z e = − n z_e=-n ze=−n 时, z n d c = − 1 z_{ndc} = -1 zndc=−1, z e = − f z_e=-f ze=−f 时, z n d c = 1 z_{ndc}=1 zndc=1。由此可以得到两个等式:
− A ∗ f + B f = 1 A ∗ n + B n = − 1 \frac{-A*f+B}{f} = 1 \\ \frac{A*n+B}{n} = -1 f−A∗f+B=1nA∗n+B=−1
解得: A = − f + n f − n A=-\frac{f+n}{f-n} A=−f−nf+n 、 B = − − 2 f n f − n B=-\frac{-2fn}{f-n} B=−f−n−2fn
最终的矩阵为:
[ n r 0 0 0 0 n t 0 0 0 0 − f + n f − n − 2 f n f − n 0 0 − 1 0 ] \left[ \begin{matrix} \frac{n}{r} & 0 & 0 & 0 \\ 0 & \frac{n}{t} & 0 & 0 \\ 0 & 0 & -\frac{f+n}{f-n} & \frac{-2fn}{f-n} \\ 0 & 0 & -1 & 0 \end{matrix} \right] rn0000tn0000−f−nf+n−100f−n−2fn0
这个矩阵,即是所谓的投影矩阵,它可以完成相机坐标系到 NDC 坐标系的转换。
对于投影点的坐标 ( x n d c , y n d c , z n d c ) (x_{ndc},y_{ndc},z_{ndc}) (xndc,yndc,zndc),如果数值超出 [-1,1] 的范围,就说明投影后的点超出了屏幕范围,可以直接舍弃。
NeRF中的NDC ray space
NeRF 中的坐标,是以射线的形式表示:o+td,其中 o 是射线起点,d 是方向向量,t 是射线长度。
所谓的 NDC ray space,就是把这种射线形式表示的坐标,从相机坐标系投影到 NDC 坐标系。因此,转换的媒介仍然是投影矩阵:
( n r 0 0 0 0 n t 0 0 0 0 − f + n f − n − 2 f n f − n 0 0 − 1 0 ) ( x y z 1 ) = ( n r x n t y − f + n f − n z − 2 f n f − n − z ) p r o j e c t → ( n r x − z n t y − z f + n f − n − 2 f n f − n 1 − z ) \left( \begin{matrix} \frac{n}{r} & 0 & 0 & 0 \\ 0 & \frac{n}{t} & 0 & 0 \\ 0 & 0 & -\frac{f+n}{f-n} & \frac{-2fn}{f-n} \\ 0 & 0 & -1 & 0 \end{matrix} \right) \left( \begin{matrix} x \\ y \\ z \\ 1 \end{matrix} \right) = \left( \begin{matrix} \frac{n}{r} x\\ \frac{n}{t}y \\ -\frac{f+n}{f-n}z - \frac{2fn}{f-n} \\ -z \end{matrix} \right) \\ project \rightarrow \left( \begin{matrix} \frac{n}{r} \frac{x}{-z}\\ \frac{n}{t}\frac{y}{-z} \\ \frac{f+n}{f-n} - \frac{2fn}{f-n}\frac{1}{-z} \end{matrix} \right) rn0000tn0000−f−nf+n−100f−n−2fn0 xyz1 = rnxtny−f−nf+nz−f−n2fn−z project→ rn−zxtn−zyf−nf+n−f−n2fn−z1
不过,由于坐标的表达形式换了,因此公式上也发生了一些变动
假设我们已经获得了相机坐标系中的坐标点
P
e
=
o
+
t
d
P_e=o+td
Pe=o+td,对应 x/y/z 轴的坐标分别为 (注意区分这里的 t 和投影平面的边界 t ):
x
e
=
o
x
+
t
∗
d
x
y
e
=
o
y
+
t
∗
d
y
z
e
=
o
z
+
t
∗
d
z
x_e = o_x+t*d_x \\ y_e = o_y+t*d_y \\ z_e = o_z+t*d_z
xe=ox+t∗dxye=oy+t∗dyze=oz+t∗dz
现在需要求出它在 NDC 坐标系中的投影坐标,假设是 P ′ = o ′ + t ′ d ′ P'=o'+t'd' P′=o′+t′d′
那么根据投影矩阵, P e P_e Pe 转换到 P’ 的过程可以表示为:
x ′ = o x ′ + t ′ ∗ d x ′ = − n r ∗ o x + t ∗ d x o z + t ∗ d z y ′ = o y ′ + t ′ ∗ d y ′ = − n t ∗ o y + t ∗ d y o z + t ∗ d z z ′ = o z ′ + t ′ ∗ d z ′ = f + n f − n + 2 f n f − n ∗ 1 o z + t ∗ d z x' = o'_x +t'*d'_x = - \frac{n}{r} * \frac{o_x+t*d_x}{o_z+t*d_z} \\ y' = o'_y +t'*d'_y = - \frac{n}{t} * \frac{o_y+t*d_y}{o_z+t*d_z} \\ z' = o'_z +t'*d'_z = \frac{f+n}{f-n} + \frac{2fn}{f-n}*\frac{1}{o_z+t*d_z} x′=ox′+t′∗dx′=−rn∗oz+t∗dzox+t∗dxy′=oy′+t′∗dy′=−tn∗oz+t∗dzoy+t∗dyz′=oz′+t′∗dz′=f−nf+n+f−n2fn∗oz+t∗dz1
为了简洁一些,假设 − n r = a x -\frac{n}{r} = a_x −rn=ax, − n t = a y -\frac{n}{t}=a_y −tn=ay, f + n f − n = a z \frac{f+n}{f-n}=a_z f−nf+n=az, 2 f n f − n = b z \frac{2fn}{f-n} = b_z f−n2fn=bz。那么上面这堆复杂的式子可以简化为:
x ′ = a x ∗ o x + t ∗ d x o z + t ∗ d z y ′ = a y ∗ o y + t ∗ d y o z + t ∗ d z z ′ = a z ∗ b z o z + t ∗ d z x' = a_x * \frac{o_x+t*d_x}{o_z+t*d_z} \\ y' =a_y * \frac{o_y+t*d_y}{o_z+t*d_z} \\ z' =a_z * \frac{b_z}{o_z+t*d_z} x′=ax∗oz+t∗dzox+t∗dxy′=ay∗oz+t∗dzoy+t∗dyz′=az∗oz+t∗dzbz
接下来就是要把 o’、t’、d’ 求解出来。
首先,对于 o’ 来说,可以直接通过 o 投影得到,即让上述公式中 t为0:
o ′ = [ o x ′ o y ′ o z ′ ] = [ a x ∗ o x o z a y ∗ o y o z a z + b z o z ] o' = \left[ \begin{matrix} o'_x \\ o'_y \\ o'_z \\ \end{matrix} \right] = \left[ \begin{matrix} a_x * \frac{o_x}{o_z} \\ a_y * \frac{o_y}{o_z} \\ a_z+\frac{b_z}{o_z} \end{matrix} \right] o′= ox′oy′oz′ = ax∗ozoxay∗ozoyaz+ozbz
在 o’确定后,t‘*d’ 可以表示为:
[
t
′
∗
d
x
′
t
′
∗
d
y
′
t
′
∗
d
z
′
]
=
[
x
′
−
o
x
′
y
′
−
o
y
′
y
′
−
o
z
′
]
\left[ \begin{matrix} t'*d'_x \\ t'*d'_y \\ t'*d'_z \end{matrix} \right] = \left[ \begin{matrix} x'-o'_x \\ y'-o'_y \\ y'-o'_z \\ \end{matrix} \right]
t′∗dx′t′∗dy′t′∗dz′
=
x′−ox′y′−oy′y′−oz′
代入
o
x
′
,
o
y
′
,
o
z
′
o'_x,o'_y,o'_z
ox′,oy′,oz′ 并化简得到

解得:
t
′
=
t
∗
d
z
o
z
+
t
∗
d
z
=
1
−
o
z
o
z
+
t
∗
d
z
d
′
=
[
a
x
∗
(
d
x
d
z
−
o
x
o
z
)
a
y
∗
(
d
y
d
z
−
o
y
o
z
)
−
b
z
∗
1
o
z
]
t' = \frac{t*d_z}{o_z+t*d_z} = 1- \frac{o_z}{o_z+t*d_z} \\ d' = \left[ \begin{matrix} a_x * (\frac{d_x}{d_z} - \frac{o_x}{o_z}) \\ a_y * (\frac{d_y}{d_z} - \frac{o_y}{o_z}) \\ -b_z*\frac{1}{o_z} \end{matrix} \right]
t′=oz+t∗dzt∗dz=1−oz+t∗dzozd′=
ax∗(dzdx−ozox)ay∗(dzdy−ozoy)−bz∗oz1
当 t = 0时,t’=0,当 t → ∞ t\rightarrow \infty t→∞ 时 t ′ → 1 t' \rightarrow 1 t′→1。所以,在相机坐标系对光线进行采样 ( t ∈ ( 0 , ∞ ) t\in(0,\infty) t∈(0,∞)),就等价于在 NDC ray space 中,对 t’ 在 [0,1] 范围内进行采样。
对于投影屏幕来说,可以设定最后成像的图片长宽 (H*W) 和屏幕大小一致,由于投影屏幕的中心即是坐标原点,因此 r=w/2 ,t=H/2。再假定相机的焦距 f c a m f_{cam} fcam 和 Near Clipping Plane 到相机中心的距离相等,即 n = f c a m n=f_{cam} n=fcam。则 a x , a y a_x,a_y ax,ay 可以重新表示为:
a x = − f c a m W / 2 a y = − f c a m H / 2 a_x = -\frac{f_{cam}}{W/2} \\ a_y = -\frac{f_{cam}}{H/2} \\ ax=−W/2fcamay=−H/2fcam
(所谓焦距,指的是相机光圈到成像平面的距离。但正如文章开始提到的,由于图形学中的相机是模拟的,所以并不存在焦距的概念。只是由于投影平面一般和 Near Clipping Plane 重合,因此可以简单认为 f c a m = n f_{cam} = n fcam=n ,但二者其实是不同的概念)
对于 a z a_z az 和 b z b_z bz ,由于论文将 f 设定为无穷远,因此:
a z = lim f → ∞ f + n f − n = lim f → ∞ ( 1 + 2 n f − n ) = 1 a_z = \lim_{f \rightarrow \infty} \frac{f+n}{f-n} \\ =\lim_{f \rightarrow \infty}(1+\frac{2n}{f-n}) \\ = 1 az=f→∞limf−nf+n=f→∞lim(1+f−n2n)=1
b z = lim f → ∞ 2 f n f − n = lim f → ∞ 2 n 1 − n f = 2 n b_z = \lim_{f \rightarrow \infty} \frac{2fn}{f-n} \\ =\lim_{f \rightarrow \infty} \frac{2n}{1-\frac{n}{f}} \\ = 2n bz=f→∞limf−n2fn=f→∞lim1−fn2n=2n
可以得到最终的 o’ 和 d’

在 t ∈ [ 0 , 1 ] t\ \in [0,1] t ∈[0,1] 内采样,等价于相机坐标系中在 t ∈ [ 0 , ∞ ] t\in[0,\infty] t∈[0,∞] 范围内采样。但是,如前文描述的,相机坐标系的可视范围是从 Near Clipping Plane 到 Far Clipping Plane 之间,也就是在 z ∈ [ − ∞ ] , − n z\in[-\infty],-n z∈[−∞],−n 这个区间。为了保证光线上每个采样点可见,需要把光线起点对齐到 Near Clipping Plane 上。
即 o 沿光线方向移动 t n t_n tn 个单位后, o z = − z o_z = -z oz=−z,表示成公式为:
o z + t n ∗ d z = − n t n = n + o z d z o_z+t_n*d_z = -n \\ t_n = \frac{n+o_z}{d_z} oz+tn∗dz=−ntn=dzn+oz
因此,移动后的光线起点为 o n = o + t n d o_n = o+t_n d on=o+tnd:




![[ 蓝桥杯Web真题 ]-组课神器](https://img-blog.csdnimg.cn/direct/c760d682770341768ffe2da6f01ba10e.gif)