目录
- 题目描述
- 输入格式
- 输出格式
- 测试样例
- 样例说明
- 思路
- 核心代码
题目描述
在 f u f u fufu fufu乐园,每天都会有各种各样精彩的内容发生。就比如说,今天,小樱的米饭店开张啦!
为了吸引 f u f u fufu fufu们前来购买小樱的大米,小樱决定设置一个问题来吸引 f u f u fufu fufu们!如果有 f u f u fufu fufu可以解决这个问题,那么这位 f u f u fufu fufu每周都可以去小樱的米饭店免费吃一次米饭大餐!当然,为了不让太多的 f u f u fufu fufu成功白嫖到小樱的大米,这个问题还是需要一些思考的!
小樱的问题是什么呢?首先,小樱会给你很多个一维数轴上线段的左端点和右端点,既然有很多个线段,那么就很可能会有交叉的地方啦!小樱的问题就是,让你求出有多少个整数被至少两个线段覆盖。同时,小樱定义了重叠部分,当一个区间至少有包含两个线段,那么这个区间就被定义为重叠部分。
众所周知,大傻最最最喜欢吃大米了,但是大傻又太傻了,解决不了小樱出的问题。大傻只知道,你最最最喜欢大傻了。为了得到更多的大米,大傻想要你帮她解决小樱的问题,使她得到每周免费吃大餐的机会。作为补偿,你可以和大傻一起去吃大米 (这可是大傻的邀请欸)!
那么,聪明的,你告诉我,你可以解决大傻的问题吗?
输入格式
第 1 1 1行包含一个整数 n n n, 表示线段的个数 第 2 2 2行至第 n + 1 n+1 n+1行,每行包含两个数 l l l和 r r r,各自代表线段的左段点和右端点
输出格式
仅输出 1 1 1个整数,代表被至少两个线段覆盖的数的数量
测试样例
3
1 4
2 5
6 9
3
6
1 10
10 20
20 30
30 40
40 50
50 60
5
3
-1 2
1 4
2 5
4
3
1 1000
500 101000
99999 1000000
1503
数据范围:
1 < = n < = 1000000 1<= n <= 1000000 1<=n<=1000000
− 1000000 < = l < r < = 1000000 -1000000<=l<r<=1000000 −1000000<=l<r<=1000000
样例说明
样例 1 1 1解释
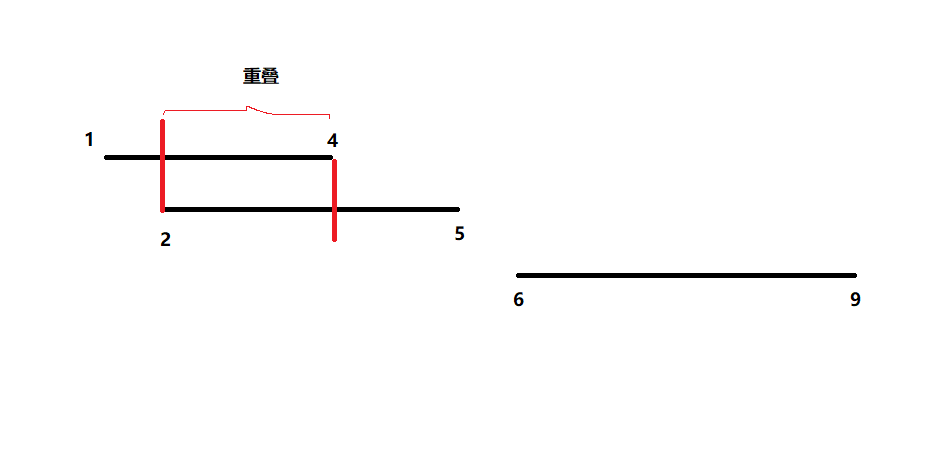
重叠部分有 [ 2 , 4 ] [2, 4] [2,4]即 2 , 3 , 4 2, 3, 4 2,3,4,答案是 3 3 3
样例 2 2 2解释
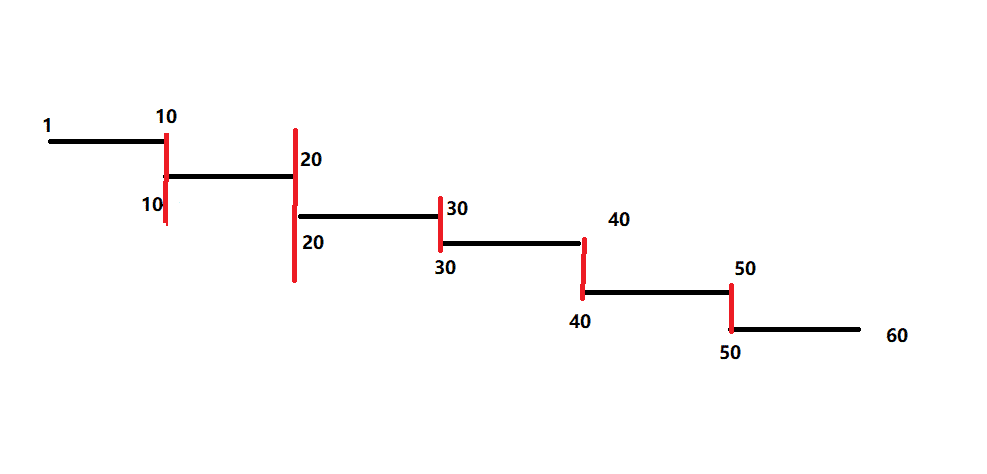
重叠部分是 [ 10 , 10 ] , [ 20 , 20 ] , [ 30 , 30 ] , [ 40 , 40 ] , [ 50 , 50 ] [10, 10], [20, 20], [30, 30], [40, 40], [50, 50] [10,10],[20,20],[30,30],[40,40],[50,50]即 10 , 20 , 30 , 40 , 50 10 ,20, 30, 40, 50 10,20,30,40,50,答案是 1 + 1 + 1 + 1 + 1 = 5 1 + 1 + 1 + 1 + 1 = 5 1+1+1+1+1=5
样例 3 3 3解释
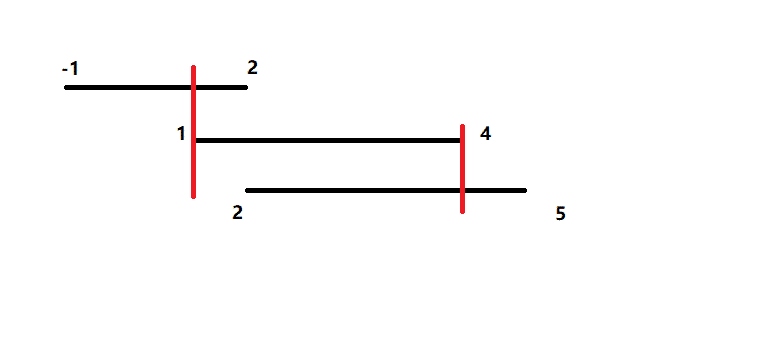
重叠部分是 [ 1 , 4 ] [1, 4] [1,4] ,即 1 , 2 , 3 , 4 1, 2, 3, 4 1,2,3,4,答案是 4 4 4
样例 4 4 4解释
重叠部分是 [ 500 , 1000 ] , [ 99999 , 101000 ] [500, 1000], [99999, 101000] [500,1000],[99999,101000]答案是 501 + 1002 = 1503 501 + 1002 = 1503 501+1002=1503

思路
这道题目是求重合的线段有多少个,本题中出现的所有的点都是整数,那我们就对线段上所有的数离散化,然后就就可以使用前缀和进行区间加法的操作,这里不难理解,因为多加上一个线段就意味着这个区间上的所有点的值需要加一。
核心代码
#include <iostream>
using namespace std;
long long arr[100000005];
int main() {
int n;
cin>>n;
long long x,y;
for(int i=0;i<n;++i)
{
scanf("%lld%lld",&x,&y);
x+=1000000;
y+=1000000;
arr[x]++;
arr[y+1]--;
}
long long sum=0;
int ans=0;
for(int i=0;i<1e7;++i)
{
sum+=arr[i];
if(sum>1)ans++;
}
cout<<ans;
return 0;
}