推文作者：Amiee，研究方向：交通物流

编者按：

VRP问题由于其理论难度和实践价值，学者们设计了大量的精确或启发式求解算法。本文讨论了车辆路径启发式中分解技术的主要特征，强调了它们的优缺点，并推导出了一组理想的性质。

摘要

分解技术是用于求解车辆路径问题的大型实例的现代启发式算法的重要组成部分。当前的文献缺乏对分解策略的描述，也缺乏对其影响的系统研究，这些研究与最先进的启发式方法相结合。本文讨论了车辆路径启发式中分解技术的主要特征，强调了它们的优缺点，并推导出了一组理想的性质。通过数值实验，分析了在两种经典算法（自适应大邻域搜索算法和混合遗传搜索）中集成分解技术对CVRP求解的影响。结果表明，基于route的分解方法优于基于Path的分解方法。

引言

VRP问题的目标是为一组在空间上离散的节点确定一条最小成本的车辆路径。因为其理论难度和实践价值，学者们设计了大量的精确或启发式求解算法。特别地，启发式算法已经被证明是求解大规模问题的有效算法，而分解策略对启发式算法的性能具有明显的影响。因此，本文主要关注以下两个方面：

• 讨论了VRP启发式分解技术的一些基本特征，其主体思路为：
  • 将实例重复分解为单独求解的较小子问题，并通过合并子问题的解，以获得原始问题的完整解。
  • 粗化聚合方法(Coarsening and aggregation)：固定某些弧段的粗化和聚合方法，它会有效减少问题中的节点数量。
  • 破坏和重建方法(Ruin-and-recreate)：暂时将一组客户和弧段保持固定，并试图重新排列其余的决策变量。
• 通过计算实验讨论不同分解技术对CVRP解的影响，重点关注了Pisinger和Ropke (2007)的自适应大邻域搜索(ALNS), 和Vidal &Thibaut(2022)的混合遗传搜索（HGS），在集成分解技术后的性能表现。

分解技术的特征

启发式分解技术具有以下四个特征：第一是分解得到的子问题的特征，第二是定义子问题用到的信息，第三是子问题的解法，第四是子问题的解应用到主问题的方式。

子问题的特征

同质分解和异质分解

• 所谓同质分解就是从原问题分解得到的子问题与原问题具有相同的结构，在这种分解模式下，通过递归地调用单一解法来求解。例如，基于顾客划分的分解带来的子问题通常是同质分解，这种分解导致了规模更小的车辆路径问题。
• 所谓异质分解是指求解子问题的算法和求解主问题的算法是不同的算法。例如，将某个距离相近聚合为宏节点(macro-nodes)的方式，可能需要为子问题定制不同的求解方案。例如，有A,B,C,D四个节点，我们将节点A和节点B聚合为宏节点，那么优化问题就变为节点C和节点D在宏节点AB之前访问还是在AB之后访问更有利。
  

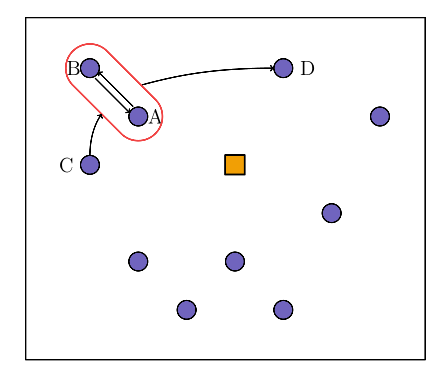
子问题是独立的还是相互依赖的

• 分解后会得到多个子问题。每个子问题的目标值和可行性，不依赖与其他子问题的目标值和可行性时，子问题间是相互独立的。大部分基于顾客划分的分解技术，产生的节点子集之间不存在交集，进而衍生出来的子问题就是相互独立的子问题。但是也有例外的情况。
• 产生依赖子问题的一类分解方法是破坏和重建算法。这些算法通过迭代破坏解决方案的一部分而其余部分保持不变来改进解决方案，这可以理解为迭代地生成并解决较小子问题的分解方法。因为从一次迭代到下一次迭代，破坏的部分之间可能存在重叠，所以这些子问题的求解通常是按顺序进行的。
• 总的来说，子问题之间相互独立的分解方式是我们希望看到的，因为它可以通过并行来减少计算时间，并且能够通过合并子问题的解来生成原问题的解。

子问题的信息

分解方法通常遵循以下三个主要原则：第一，分解产生的固定变量应支持高质量的求解方法，第二子问题的自由变量不能太多或太少，第三是自由变量应该是相关的。

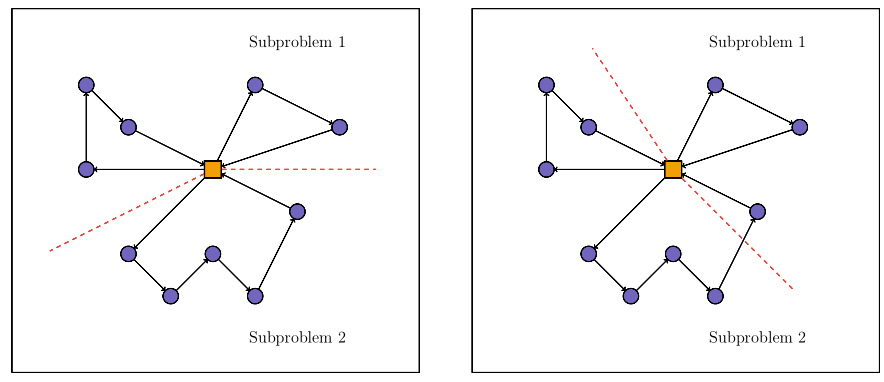
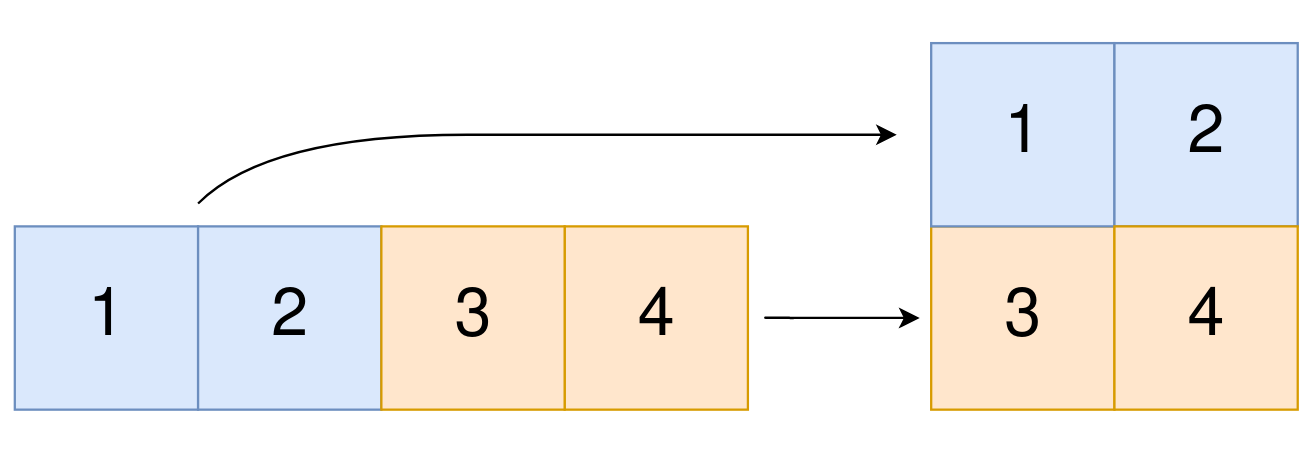
• 第一是分解是否支持精英解决方案。也就是说，我们是通过高质量的解决方案来定义子问题。如下图，左侧的图中，分解之后的子问题不会破坏精英解决方案，此时分解策略支持精英解决方案；而在右侧图中，分解后的子问题会破坏精英解决方案，此时分解策略不支持精英解决方案。

• 第二是子问题的规模，它是控制子问题难度和改进潜力的重要参数，子问题规模的大小取决于算法的性能（包括计算时间和解决方案的质量）。子问题的规模可以是固定的，也可以是随机的，还可以是根据算法的某些指标在搜索过程中动态变化。当可以精确地知道算法求解子问题的能力时，可以选择固定大小模式。但是如果不知道这样的信息，或者子问题规模的细微变化会对算法的性能产生重大影响时，自适应地确定子问题的规模则是一个更好地选择。

• 第三是关联信息。子问题的创建可能用到一些关联信息，如节点间的空间关联、时间关联、历史关联和解的模式关联等。空间和时间相关性度量直接源自问题的特征，并测量两个节点在空间或时间上的接近程度。相比之下，历史关联和解的模式关联，则考察了在历史搜索中，在得到的较好的解决方案中，某些决策被同时做出的频率。

子问题的求解技术

不同的子问题求解技术，在运行时间和解决方案质量上可能有很大差异。子问题的求解技术的范畴包括从简单的贪婪启发式到复杂的元启发式的启发式谱系，和从隐式枚举到分支定价技术的精确算法谱系。
求解算法的运行时间和解的质量是密切相关的，在破坏重建型算法中，使用贪婪启发式方法的好处在于很快能得到一个新的解，但产生良好解决方案的概率随着子问题的大小而迅速降低。同时，随着基于分支定价技术的精确算法在获取精确解的能力方面的改善，在子问题的求解中，探索使用基于精确算法处理子问题的新型分解算法，展现出了很好的前景。

子问题解的用处

当定义的子问题支持精英解时，直接替换或改进精英解即可。因此，推荐使用具有独立特征和同质分解结构，且支持精英解决方案的启发式分解技术；在这种情形下，可充分的利用子问题的解。

分解技术的设计

基于此思路，重点考虑了两种启发式分解技术，第一是基于Route的分解，这种模式是基于精英路径来定义子问题；第二是基于Path的分解，迭代地规定某些节点序列。

基于Route的分解

基于Route的分解方法创建一组独立的子问题S={S_{1},…,S_{k}}，然后通过递归地求解每一个子问题，之后合并子问题的解即可重建出原始问题的解。每个子问题可以定义为S_{j}={V_{j},p_{j}}，其中V_{j}表示构成子问题的节点集合，p_{j}表示该子问题中包含的车辆数目。

对于CVRP，它的解可表示为一个路径集，每条路径包含一组节点，如果车辆没有被使用，则对应子问题包含的节点集合为空，车辆数目为0。

基于Path的分解

基于Path的分解的思路是将一组节点T=(v_{1},…,v_{r})合并为一个宏节点v_{T}，从而来定义子问题。宏节点内部将对应一个访问序列，假设为(v_{1},…,v_{r})，也即Path。基于Path，则有：

• 宏节点的需求量等于组成宏节点的所有节点的需求量之和
• 宏节点与不在宏节点内的其他节点u\in V-T之间的行驶成本为c_{u,v_{T}}=c_{u,v_{1}}和c_{v_{T}，u}=c_{v_{r},u}。
• 宏节点处的服务时间为内部节点的行驶时间之和。

在这种分解方式下，利用宏节点定义削减的子问题(reduced subproblem)，在求解完子问题后，将子问题的解替换到原问题解的对应部分。这种分解其实可以理解为，从精英解中抽取一部分节点，来定义子问题。如果每个宏节点只包含一个节点，则相当于是抽取了单个弧段。

集成分解技术的ALNS设计

ALNS算法通过迭代地调用破坏和修复算子来快速求解大规模的路径问题，其中破坏算子移除了解的一部分节点，而修复算子重建了破坏算子产生的部分解。在ALNS集成分解技术的一个简单实现为，每隔固定的次数，对当前最优解执行一次分解。

基于分解技术的混合遗传搜索（HGS）

HGS是一种为各种VRP设计的遗传算法，它与经典遗传算法的区别是，对种群多样性进行了更高层级的管理。该算法允许可行解和不可行解在种群中共存。解决方案的适应度是根据其成本、对可能不可行的惩罚以及对其对种群多样性贡献的奖励来计算的。类似地，集成分解策略的HGS的一个简单实现为，每隔固定的次数，对当前最优解执行一次分解。

结论

经过测试，基于Route的分解方法通常优于基于Path分解方法。这样的结论为未来的研究工作带来许多新的潜能，例如可以使用复杂的学习机制和稀疏化( sparsification)技术来更好的定义子问题；并且随着CVRP及其子问题的数学规划的重大进展，利用精确技术处理分解子问题，也可能在未来表现出更大的潜力。

参考文献

Santini, A., Schneider, M., Vidal, T., & Vigo, D. (2023). Decomposition strategies for vehicle routing heuristics. INFORMS Journal on Computing. doi：https://doi.org/10.1287/ijoc.2023.1288