更多资料获取

📚 个人网站：ipengtao.com

---

当处理迷宫问题时，遗传算法提供了一种创新的解决方案。本文将深入探讨如何运用Python和遗传算法来解决迷宫问题。迷宫问题是一个经典的寻路问题，寻找从起点到终点的最佳路径。遗传算法是一种启发式优化方法，适用于解决复杂问题，其中个体进化和自然选择的概念被用于寻找最优解。

通过Python的代码示例和解释，将展示遗传算法如何在迷宫问题中发挥作用。此外，本文还将解释如何建模迷宫、编码迷宫路径、设计适应度函数以及实现遗传算法的选择、交叉和变异操作。

迷宫建模

当建模迷宫时，可以使用二维数组来表示不同的迷宫区域，如墙壁、路径、起点和终点。以下是一个示例的Python代码：

# 0 表示可通行的路径
# 1 表示墙壁
# S 表示起点
# E 表示终点

maze = [
    [1, 1, 1, 1, 1, 1, 1],
    [1, 0, 0, 0, 0, 0, 1],
    [1, 0, 1, 1, 1, 0, 1],
    [1, 0, 0, 0, 0, 0, 1],
    [1, 1, 1, 1, 1, 0, 1],
    [1, 'S', 0, 0, 0, 0, 1],
    [1, 1, 1, 1, 1, 1, 1]
]

上述代码使用数字和字符表示不同类型的迷宫区域。其中，0表示可通行的路径，1表示墙壁，'S’表示起点，'E’表示终点。这种表示方法使得迷宫的结构清晰，并便于编写寻路算法。将迷宫抽象成二维数组，可以更轻松地进行路径搜索和分析。

遗传算法基础

遗传算法是一种基于生物进化过程的优化方法，通常用于解决搜索和优化问题。其基本原理涵盖个体编码、选择、交叉和变异。

基本原理

1. 个体编码：在迷宫问题中，个体编码可以表示为一串代表移动方向的序列。例如，使用字符串（比如"DDRRUULDL"）来代表向下、向右、向上、向左的移动。

2. 选择：在遗传算法中，优秀的个体通常更有可能被选择为下一代的父代。这涉及到通过一种适应度函数来评估每个个体的性能。

3. 交叉：被选中的个体会以某种方式进行“交叉”，从而生成下一代个体。在迷宫问题中，交叉可以是路径序列的交换和组合，以产生新的路径。

4. 变异：随机性是遗传算法的一个关键部分。在交叉后，一些新个体可能会经历变异操作，以增加搜索空间。对于迷宫问题，变异可以是路径序列中某些步骤的随机变动。

解决迷宫问题

使用遗传算法解决迷宫问题涉及将上述原理应用到迷宫的搜索过程中。基于迷宫的二维数组表示，个体编码将是代表路径的序列。适应度函数将评估路径的有效性和质量，即路径是否能成功走出迷宫。选择、交叉和变异操作将在不断迭代中产生出下一代更优秀的路径，最终找到出路。

结合遗传算法的基本原理和迷宫问题的特点，可以设计一个自定义的遗传算法来解决迷宫问题，找到最优路径以走出迷宫。

编码个体

在遗传算法中，编码迷宫路径可以采用字符串表示路径的方向。例如，用单个字符串来表示移动的方向，其中每个字符代表一种移动方向。

在迷宫问题中，可以使用以下方式编码迷宫路径：

• D：向下移动
• U：向上移动
• L：向左移动
• R：向右移动

例如，一个路径编码可能如下所示：

path = "DDRURULDL"

上述编码表示从起点到终点的一条路径，其中每个字符代表了在迷宫中的一个移动方向。在迷宫问题中，将这样的路径编码与遗传算法相结合，通过选择、交叉和变异操作，逐步寻找最佳路径以走出迷宫。

适应度函数

适应度函数在遗传算法中扮演着至关重要的角色。它用于评估每条路径的优劣，并决定哪些路径更有可能被选择进入下一代。在迷宫问题中，适应度函数将评估路径是否能够成功通向迷宫出口。

下面是一个简单的示例，演示如何编写一个适应度函数来评估迷宫路径的优劣：

def fitness_function(path, maze):
    # 获取起点坐标
    start = find_starting_point(maze)
    
    x, y = start[0], start[1]
    
    # 按路径移动
    for move in path:
        if move == 'D':
            x += 1
        elif move == 'U':
            x -= 1
        elif move == 'L':
            y -= 1
        elif move == 'R':
            y += 1
        
        # 检查是否越界或撞墙
        if x < 0 or y < 0 or x >= len(maze) or y >= len(maze[0]) or maze[x][y] == 1:
            return 0  # 无效路径，返回适应度为0
    
        # 到达终点
        if maze[x][y] == 'E':
            return 1  # 成功到达终点，返回适应度为1
            
    return 0  # 路径未到达终点，返回适应度为0

适应度函数的基本思路是按照路径移动，检查路径是否越界、撞墙或成功到达终点。如果路径能够成功通向迷宫的出口，适应度函数返回一个较高的值（如1），否则返回较低的值（如0）。通过这样的适应度函数，可以评估路径的有效性，并在遗传算法中筛选出更优秀的路径。

选择、交叉和变异

在遗传算法中，选择、交叉和变异是重要的操作，用于产生新的路径。这些操作基于已有的路径，通过一定的机制生成下一代的路径。

选择（Selection）

选择操作根据路径的适应度函数对现有路径进行筛选，挑选出更适应迷宫的路径作为父代。一个简单的选择方法是基于路径的适应度函数进行随机选择或按照适应度函数排序选择。

def selection(population, maze):
    # 根据适应度函数对路径进行排序或随机选择
    # 选择较优秀的路径作为父代
    # 返回父代路径集合
    pass

交叉（Crossover）

交叉操作是将两个父代路径交叉产生新的子代路径。在迷宫问题中，交叉可以是对两个路径的某个位置进行切割并交换部分路径。

def crossover(parent1, parent2):
    # 对父代路径进行交叉操作
    # 产生子代路径
    # 返回子代路径
    pass

变异（Mutation）

变异操作是为了增加种群的多样性，对部分路径进行随机变动。在迷宫问题中，变异可以是路径序列中某些步骤的随机变动。

def mutation(path):
    # 对路径进行变异操作
    # 产生新的路径
    # 返回变异后的路径
    pass

这些操作相互作用，通过选择、交叉和变异不断迭代，产生新的路径，最终找到适应度更高的路径，以解决迷宫问题。综合使用这些操作可以提高寻找到最优路径的可能性。

迷宫求解

在迷宫问题中，使用遗传算法搜索最佳路径是一个有趣而挑战性的过程。通过综合选择、交叉和变异操作，可以编写一个迷宫求解函数，该函数利用遗传算法来寻找最佳路径。

以下是一个示例，展示如何使用遗传算法求解迷宫问题：

def solve_maze(maze, population_size, generations):
    population = generate_initial_population(population_size, maze)  # 生成初始种群

    for generation in range(generations):
        parents = selection(population, maze)  # 选择父代
        new_population = []

        for i in range(0, len(parents), 2):
            parent1 = parents[i]
            parent2 = parents[i + 1] if i + 1 < len(parents) else parents[i]

            child = crossover(parent1, parent2)  # 交叉操作
            if random_chance_of_mutation():  # 变异操作
                child = mutation(child)

            new_population.append(child)

        population = new_population  # 更新种群

        # 找到最优路径
        best_path = max(population, key=lambda path: fitness_function(path, maze))
        if fitness_function(best_path, maze) == 1:  # 如果找到最佳路径
            return best_path

    return None  # 未找到最佳路径

这段代码中的 solve_maze 函数使用遗传算法来搜索最佳路径。它包含了种群初始化、选择、交叉、变异等操作，并循环进行多代迭代以寻找最优路径。最终，它会返回找到的最佳路径或 None（如果没有找到解决方案）。

结果展示

展示最优路径和在迷宫中标记路径走向可以通过图形化展示来呈现。这需要使用相应的可视化工具和技术。

下面是一个基本示例，演示如何展示最优路径并在迷宫中标记路径走向：

import matplotlib.pyplot as plt

def display_solution(maze, best_path):
    # 标记迷宫
    for i in range(len(maze)):
        for j in range(len(maze[0])):
            if maze[i][j] == 1:  # 墙壁
                plt.fill([j, j+1, j+1, j], [len(maze) - i, len(maze) - i, len(maze) - i + 1, len(maze) - i + 1], 'black')

    # 标记路径
    x, y = find_starting_point(maze)
    for move in best_path:
        if move == 'D':
            x += 1
        elif move == 'U':
            x -= 1
        elif move == 'L':
            y -= 1
        elif move == 'R':
            y += 1

        plt.fill([y, y+1, y+1, y], [len(maze) - x, len(maze) - x, len(maze) - x + 1, len(maze) - x + 1], 'green')

    plt.show()

在这个示例中，使用了 matplotlib 库来绘制迷宫和标记路径。display_solution 函数接受迷宫和找到的最佳路径作为参数，并在图形中用不同的颜色标记出迷宫中的墙壁和最佳路径。

总结

遗传算法在解决迷宫问题中展现出了灵活性和适用性。通过编码、选择、交叉和变异等操作，遗传算法能够寻找到迷宫中的最佳路径。遗传算法利用了进化的思想，通过不断迭代和进化，从初始种群中产生新的路径，并筛选出更优秀的路径。这种迭代过程使得算法能够逐步优化路径，找到迷宫的出口。其优势在于可以处理多样性、搜索空间大、应对复杂情况等。然而，也需要根据具体问题调整参数和方法以获得更好的效果。

总体而言，遗传算法作为一种搜索和优化的方法，在解决迷宫问题等特定领域具有广泛的应用前景。通过本文的介绍，可以更好地理解遗传算法，并将其应用于类似问题的求解中。

---

Python学习路线

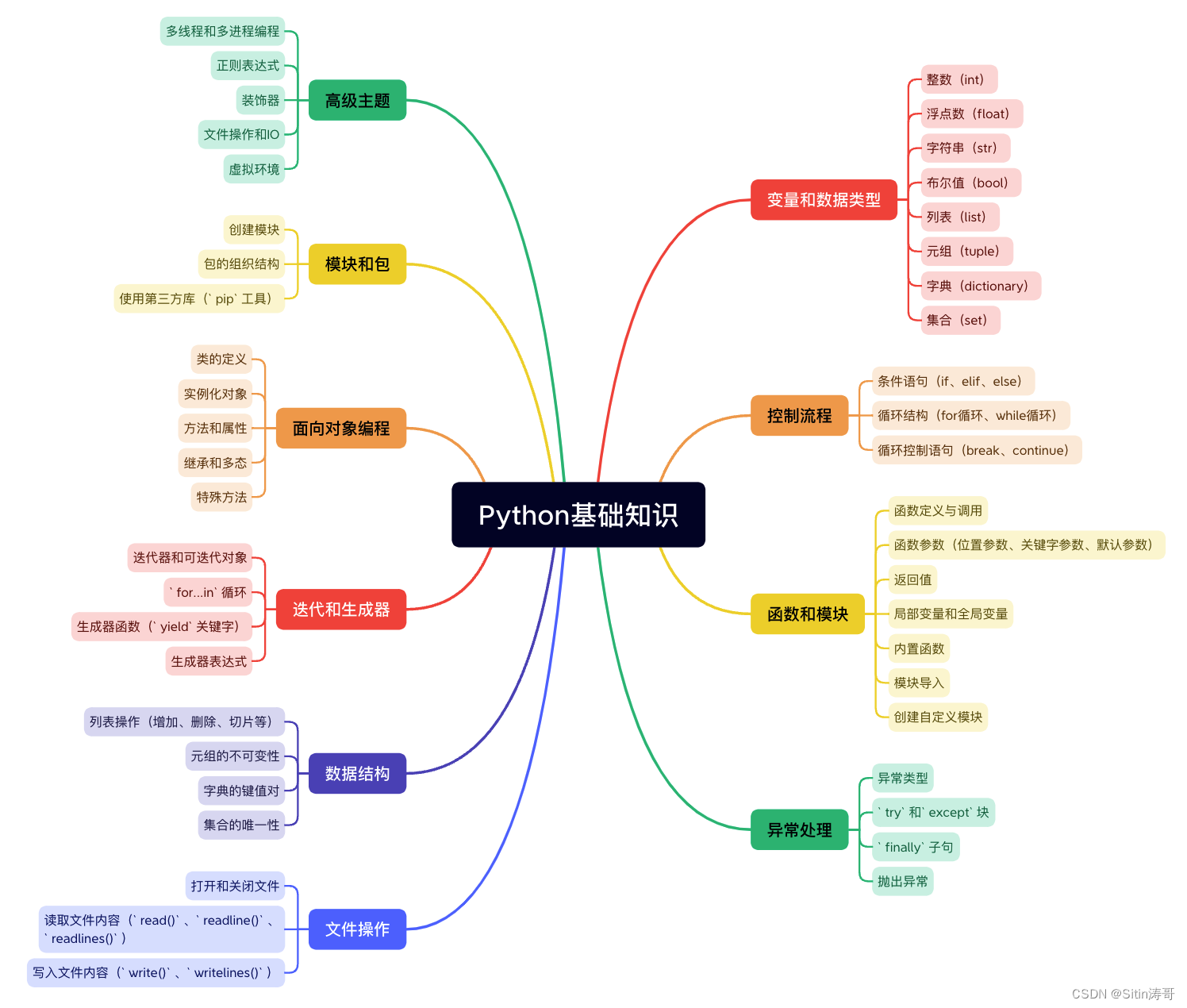
更多资料获取

📚 个人网站：ipengtao.com

如果还想要领取更多更丰富的资料，可以点击文章下方名片，回复【优质资料】，即可获取 全方位学习资料包。

点击文章下方链接卡片，回复【优质资料】，可直接领取资料大礼包。