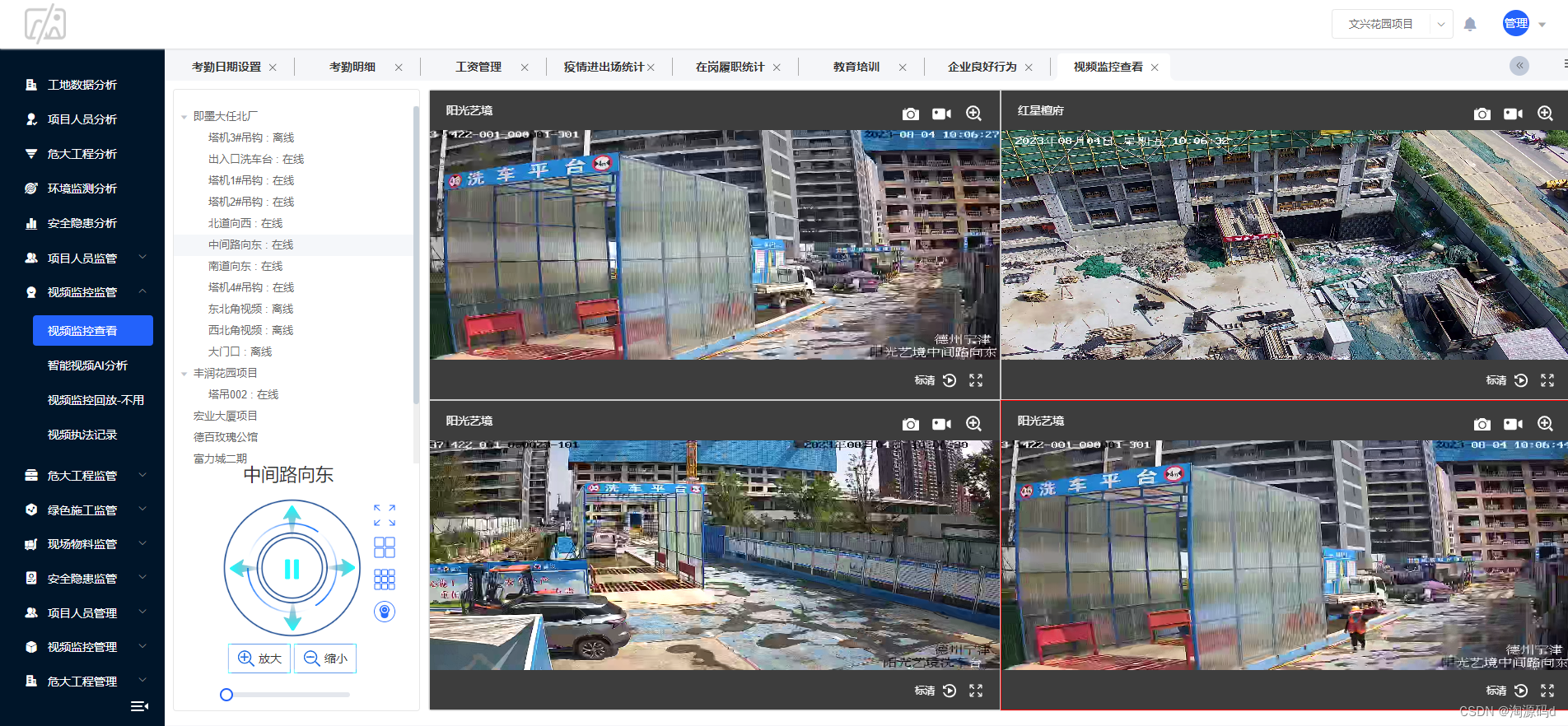
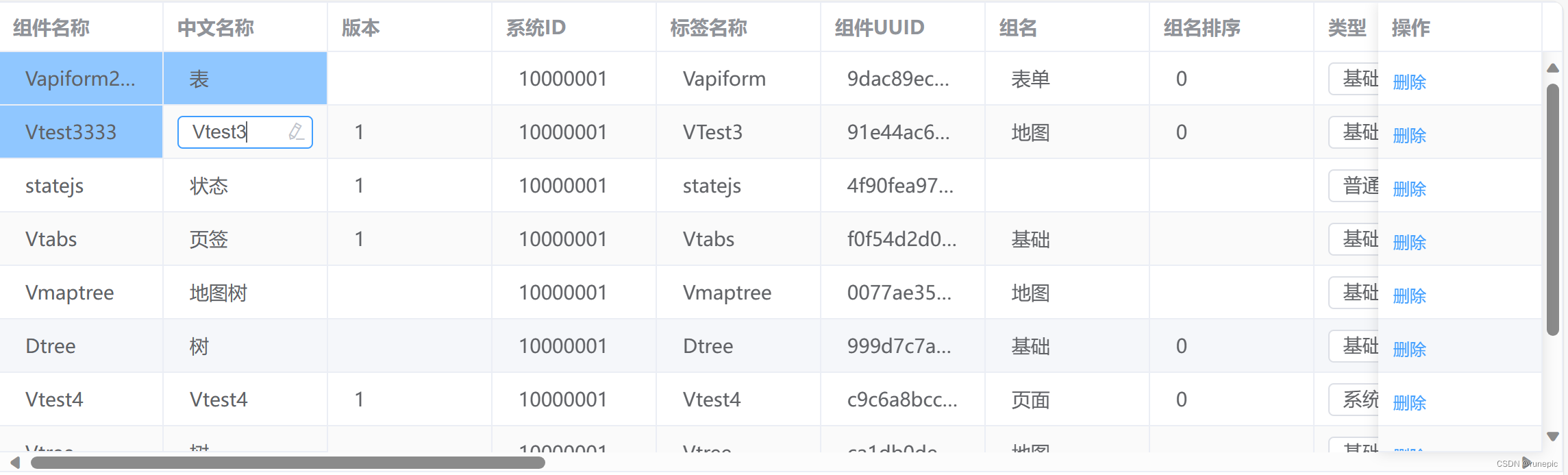
首先需要花大约20分钟来思考解决这个问题，如果对问题不是很熟悉，也可以在完成题目之后，找相关的资料翻阅（例如看UML类图的基本情况，UML状态图的基本情况，然后结合这些信息 做一个自我评价，看这个题目的相关知识是否掌握透彻），然后再看分析与讲解。在看分析与讲解的时候，需要注意分析的思路比这道提的答案更重要一些。

可以在图上标注：

首先，继承关系是很具有代表性的，因为在整个题干描述中，只有一个地方存在继承关系：

艺术家分为乐队和歌手，歌手乐队都属于艺术家，因此艺术家和歌手乐队直接存在继承关系。

艺术家是父类，乐队和歌手是子类。

所以A是艺术家。

那么D和C必然有一个是乐队一个是歌手。那么根据关系来判断，C和D直接是聚合关系，多个歌手聚合为一个乐队，那么根据空心菱形的方向，空心菱形指向的是整体部分，所以C是乐队，D是歌手。无论编写和演奏，都是由艺术家来做的，那么编写演奏的是什么呢？所以B是歌曲，歌曲是放在哪里的呢？根据描述，所以唱片包含了音轨，音轨包含了歌曲。E是音轨，F是唱片。因为唱片是整体部分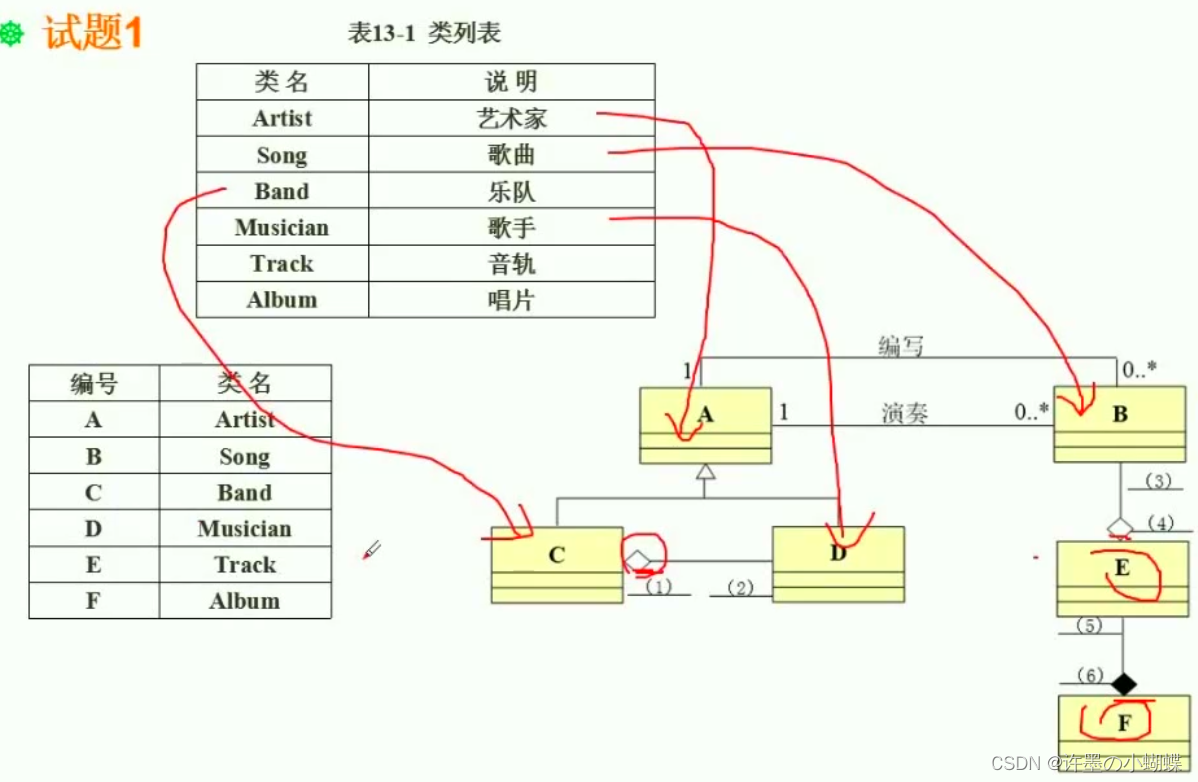

问题2：

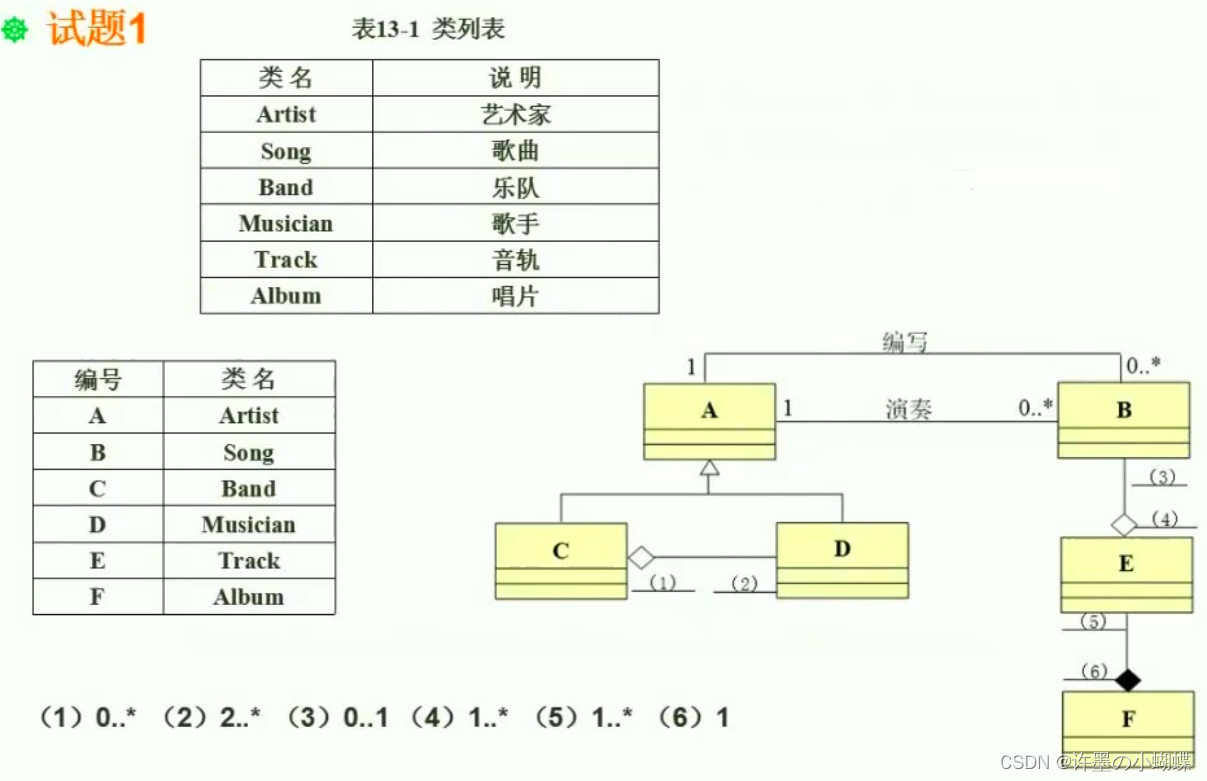
根据题目中的描述,给出图13-1中的1~6的处的多重度。

首先看C和D的关系：

D是乐队，是由2名或2名以上的歌手组成，那么（2）就是2..*， 反过来，一名歌手对应的乐队是怎么样的呢？是不是一名歌手就对应一个乐队呢？

歌手和乐队的关系： 一名歌手可以不属于任何一个乐队，也可以属于一个或多个乐队。

那么（1）就是0..*

我们判断多重度的时候，站在C的纬度来看一个乐队对应多少歌手，然后确定2处多重度是什么，然后站在D的角度来看一个歌手对应多少个乐队来确认1的位置的多重度。是从2个角度来看待问题和分析问题。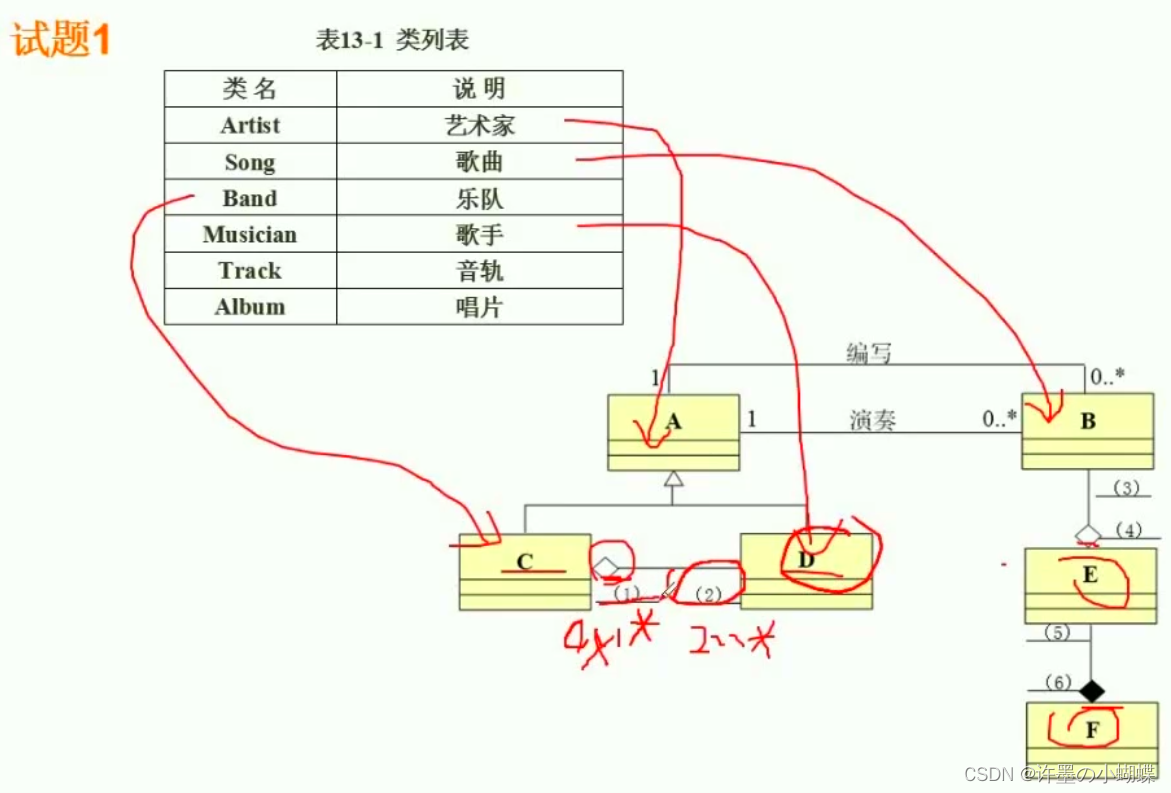

继续看B E F之 间的关系，看B和E之间的关系，也就是歌曲和音轨的关系，一条音轨包含一首歌曲或为空。那么3位置是0..1,一首歌曲可以分布在多条音轨上，那么4位置是1..*(注意如果包含0那么就没有意义了，所以不包含0）

一张唱片可以有多条音轨，也就是1条或多条。一条音轨只能在一张唱片上出现。那么5位置是1..*, 6位置是1

问题3：

图13-1中缺少了一条关联，请住处这条关联两端所对应的类以及每一端的多重度。

分析： 缺了关联，要从整个题干来分析，题干的1 2段落的内容都表现在图里了，继续往下看，发现 一条音轨和上一条音轨或者下一条音轨需要创建联系，关系是0-1，因为音轨如果有上一条或者下一条，那么就对应了上一条或下一条音轨，如果没有的话，就是0的情况。所以答案是0-1的多重度，两端都是音轨。

问题4：

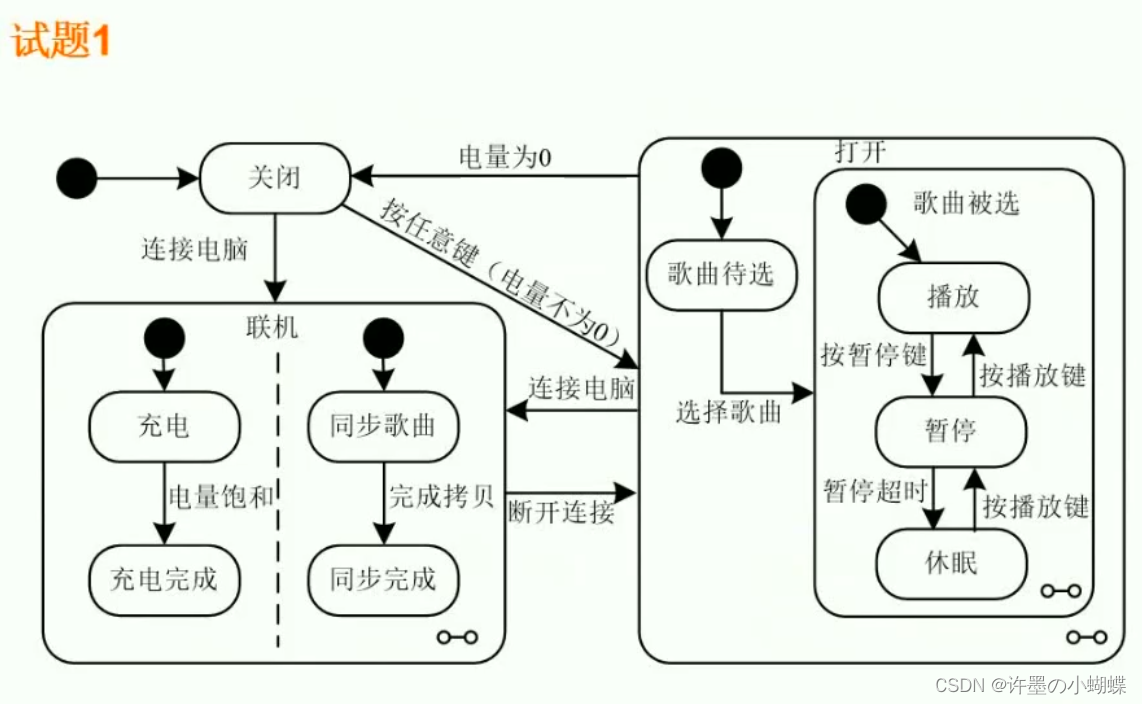
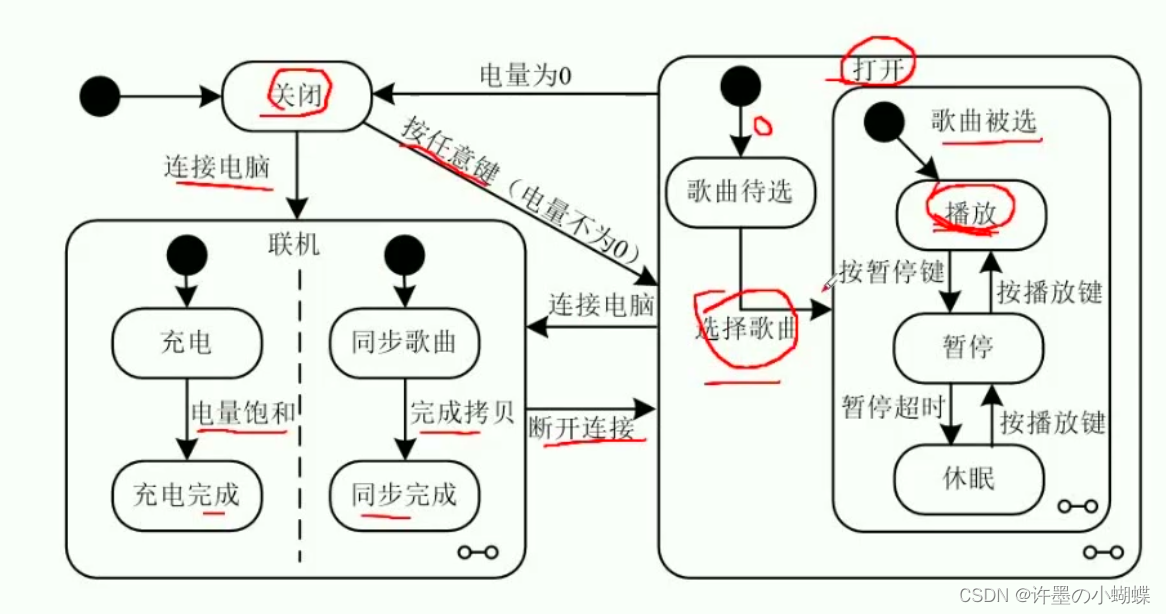
根据图13-2所示的播放器行为UML状态图，给出从关闭状态到播放状态所经过的最短事件序列。（假设电池一开始就是有电的）

根据图，标注起点“关闭”，终点“播放”，可以知道一条路径是按任意键，打开，歌曲选择，播放。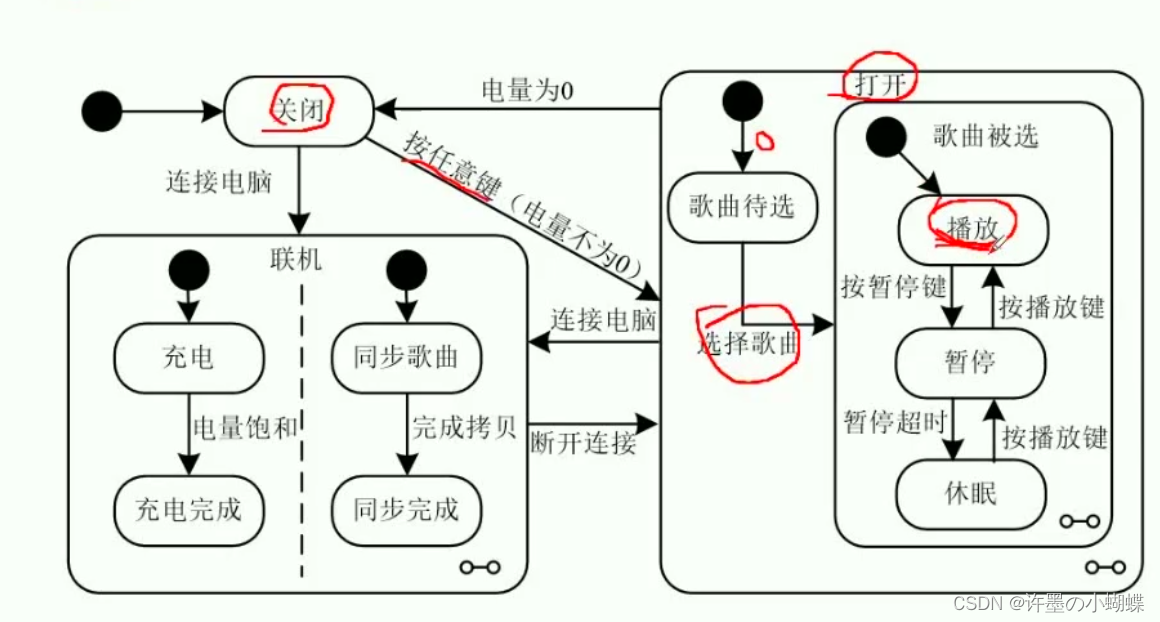

另一条路径是连接电脑，充电或同步歌曲，进入完成状态，断开连接，打开，歌曲选择，播放，可以知道按任意键是最短的路径。

根据做案例题，发现UML类型的题难度不高，可能出现的图有2种，少的时候需要1种，多的时候3种。所以要求大家对UML常见的类型图有一个基本的认识否则不知道这个图表达的是什么意思，也就无从解决问题，但是对图有一个基本的概念的认知，要解答这种问题本身技术难度并不高。