线性回归算法-实战-房价预测

本次使用线性回归的算法和knn算法进行对比
- 加载并处理数据
- 对数据进行归一化处理
- 数据拆分
- knn模型对象创建和训练
- 线性回归建模和训练
加载并且处理数据
import numpy as np
import pandas as pd
from sklearn.neighbors import KNeighborsRegressor
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
记载数据
# 加载数据
data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
target = raw_df.values[1::2, 2]
display(data.shape, target.shape)
对数据进行归一化处理
# 数据的归一化处理 正态分布
from sklearn.preprocessing import StandardScaler
# 创建对象
scaler = StandardScaler()
X = scaler.fit_transform(data)
X
数据拆分
# 数据拆分
x_train, x_test, y_train, y_test = train_test_split(X, target, test_size=0.2, random_state=1024)
knn模型对象创建和训练
%%time
knn = KNeighborsRegressor()
params = {'n_neighbors': [3, 5, 7, 9, 11, 15, 19, 23, 31],
'weights': ["uniform", 'distance'],
'p': [1, 2]}
gCV = GridSearchCV(knn, params, cv=5, scoring="neg_root_mean_squared_error")
gCV.fit(x_train,y_train)
获取knn算法决定性参数和训练参数
gCV.best_params_
gCV.score(x_test,y_test)
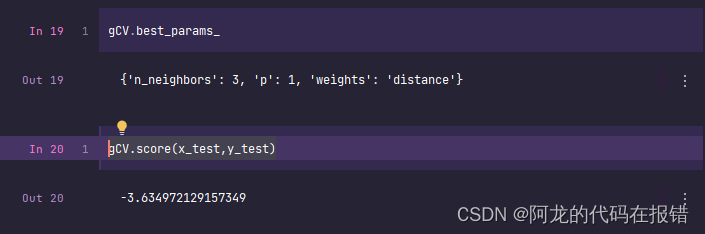
线性回归建模和训练
# 正规方程
model = LinearRegression()
model.fit(x_train,y_train)
# 决定系数最大值为1 ,最小可以是负数
model.score(x_test,y_test)
0.7259630925033402
这组波士顿房价的数据,形状偏向于正态分布所以使用线性回归的算法比较合适
The coefficient of determination :math:
R
2
R^2
R2 is defined as
:math:
(
1
−
u
v
)
(1 - \frac{u}{v})
(1−vu), where :math:u is the residual
sum of squares
(
(
y
t
r
u
e
−
y
p
r
e
d
)
∗
∗
2
)
.
s
u
m
(
)
((y_true - y_pred)** 2).sum()
((ytrue−ypred)∗∗2).sum() and :math:v
is the total sum of squares
(
(
y
t
r
u
e
−
y
t
r
u
e
.
m
e
a
n
(
)
)
∗
∗
2
)
.
s
u
m
(
)
((y_true - y_true.mean()) ** 2).sum()
((ytrue−ytrue.mean())∗∗2).sum().
The best possible score is 1.0 and it can be negative (because the
model can be arbitrarily worse). A constant model that always predicts
the expected value of y, disregarding the input features, would get
a :math:
R
2
R^2
R2 score of 0.0.
我给百度翻译了一下子
决定系数 :math:
R
2
R^2
R2 定义为
:math:
(
1
−
u
v
)
(1 - \frac{u}{v})
(1−vu),其中 :math:‘u’ 是残差
平方和
((
y
t
r
u
e
−
y
p
r
e
d
)
∗
∗
2
)
.
s
u
m
()
((y_true - y_pred)** 2).sum()
((ytrue−ypred)∗∗2).sum() 和 :math:‘v’
是平方
((
y
t
r
u
e
−
y
t
r
u
e
.
m
e
a
n
())
∗
∗
2
)
.
s
u
m
()
((y_true - y_true.mean()) ** 2).sum()
((ytrue−ytrue.mean())∗∗2).sum() 的总和。
最好的分数是 1.0,它可以是负数(因为
模型可以任意更差)。始终预测的常量模型
“y”的期望值,不考虑输入要素,将得到
A :math:
R
2
R^2
R2 得分为 0.0。
坚持学习,整理复盘