目录

一、 Kennard-Stone算法原理（KS算法）

二、Kennard-Stone算法作用

三、代码

四、对选出来的train样本使用T-SNE算法进行绘制

五、参考链接

---

一、 Kennard-Stone算法原理（KS算法）

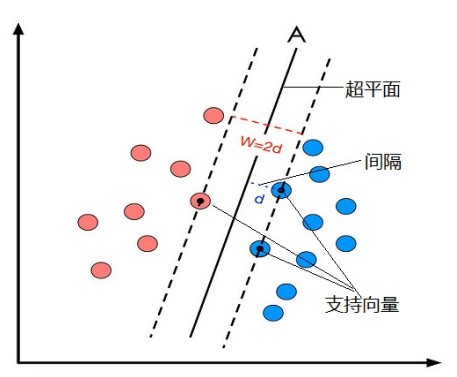
KS算法原理：把所有的样本都看作训练集候选样本,依次从中挑选样本进训练集。首先选择欧氏距离最远的两个样本进入训练集，其后通过计算剩下的每一个样品到训练集内每一个已知样品的欧式距离，找到距已选样本最远以及最近的两个样本，并将这两个样本选入训练集，重复上述步骤直到样本数量达到要求。

欧式距离计算公式：

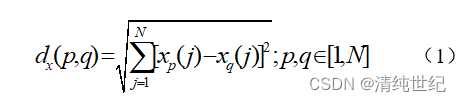
Xp，Xq表示两个不同的样本，N代表样本的光谱波点数量

二、Kennard-Stone算法作用

Kennard-Stone算法作用：用于数据集的划分，使用算法，将输入的数据集划分为训练集、测试集，并同时输出训练集和测试集在原样本集中的编号信息，方便样本的查找。

三、代码

版本1、返回样本索引：

# select samples using Kennard-Stone algorithm
import numpy as np


# --- input ---
# X : dataset of X-variables (samples x variables)
# k : number of samples to be selected
#
# --- output ---
# selected_sample_numbers : selected sample numbers (training data)
# remaining_sample_numbers : remaining sample numbers (test data)

def kennardstonealgorithm(x_variables, k):
    x_variables = np.array(x_variables)
    original_x = x_variables
    distance_to_average = ((x_variables - np.tile(x_variables.mean(axis=0), (x_variables.shape[0], 1))) ** 2).sum(
        axis=1)
    max_distance_sample_number = np.where(distance_to_average == np.max(distance_to_average))
    max_distance_sample_number = max_distance_sample_number[0][0]
    selected_sample_numbers = list()
    selected_sample_numbers.append(max_distance_sample_number)
    remaining_sample_numbers = np.arange(0, x_variables.shape[0], 1)
    x_variables = np.delete(x_variables, selected_sample_numbers, 0)
    remaining_sample_numbers = np.delete(remaining_sample_numbers, selected_sample_numbers, 0)
    for iteration in range(1, k):
        selected_samples = original_x[selected_sample_numbers, :]
        min_distance_to_selected_samples = list()
        for min_distance_calculation_number in range(0, x_variables.shape[0]):
            distance_to_selected_samples = ((selected_samples - np.tile(x_variables[min_distance_calculation_number, :],
                                                                        (selected_samples.shape[0], 1))) ** 2).sum(
                axis=1)
            min_distance_to_selected_samples.append(np.min(distance_to_selected_samples))
        max_distance_sample_number = np.where(
            min_distance_to_selected_samples == np.max(min_distance_to_selected_samples))
        max_distance_sample_number = max_distance_sample_number[0][0]
        selected_sample_numbers.append(remaining_sample_numbers[max_distance_sample_number])
        x_variables = np.delete(x_variables, max_distance_sample_number, 0)
        remaining_sample_numbers = np.delete(remaining_sample_numbers, max_distance_sample_number, 0)

    return selected_sample_numbers, remaining_sample_numbers

np.random.seed(0)
a = np.random.random((100,125))
b = np.random.randint(0,5,(100,))
selected_sample_numbers, remaining_sample_numbers = kennardstonealgorithm(a,80)

print(remaining_sample_numbers)

版本2、直接返回划分好的训练和测试样本：

import numpy as np

def ks(x, y, test_size=0.2):
    """
    :param x: shape (n_samples, n_features)
    :param y: shape (n_sample, )
    :param test_size: the ratio of test_size (float)
    :return: spec_train: (n_samples, n_features)
             spec_test: (n_samples, n_features)
             target_train: (n_sample, )
             target_test: (n_sample, )
    """
    M = x.shape[0]
    N = round((1 - test_size) * M)
    samples = np.arange(M)

    D = np.zeros((M, M))

    for i in range((M - 1)):
        xa = x[i, :]
        for j in range((i + 1), M):
            xb = x[j, :]
            D[i, j] = np.linalg.norm(xa - xb)

    maxD = np.max(D, axis=0)
    index_row = np.argmax(D, axis=0)
    index_column = np.argmax(maxD)

    m = np.zeros(N)
    m[0] = np.array(index_row[index_column])
    m[1] = np.array(index_column)
    m = m.astype(int)
    dminmax = np.zeros(N)
    dminmax[1] = D[m[0], m[1]]

    for i in range(2, N):
        pool = np.delete(samples, m[:i])
        dmin = np.zeros((M - i))
        for j in range((M - i)):
            indexa = pool[j]
            d = np.zeros(i)
            for k in range(i):
                indexb = m[k]
                if indexa < indexb:
                    d[k] = D[indexa, indexb]
                else:
                    d[k] = D[indexb, indexa]
            dmin[j] = np.min(d)
        dminmax[i] = np.max(dmin)
        index = np.argmax(dmin)
        m[i] = pool[index]

    m_complement = np.delete(np.arange(x.shape[0]), m)

    spec_train = x[m, :]
    target_train = y[m]
    spec_test = x[m_complement, :]
    target_test = y[m_complement]
    return spec_train, spec_test, target_train, target_test

np.random.seed(0)
a = np.random.random((100,125))
b = np.random.randint(0,5,(100,))
print(b)
spec_train, spec_test, target_train, target_test = ks(a,b)
print(spec_train.shape,target_train.shape)
print(spec_test.shape,target_test.shape)

四、对选出来的train样本使用T-SNE算法进行绘制

# -*- coding: utf-8 -*- %reset -f
import numpy as np
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE

# --- input ---
# X : dataset of X-variables (samples x variables)
# k : number of samples to be selected
#
# --- output ---
# selected_sample_numbers : selected sample numbers (training data)
# remaining_sample_numbers : remaining sample numbers (test data)

def kennardstonealgorithm(x_variables, k):
    x_variables = np.array(x_variables)
    original_x = x_variables
    distance_to_average = ((x_variables - np.tile(x_variables.mean(axis=0), (x_variables.shape[0], 1))) ** 2).sum(
        axis=1)
    max_distance_sample_number = np.where(distance_to_average == np.max(distance_to_average))
    max_distance_sample_number = max_distance_sample_number[0][0]
    selected_sample_numbers = list()
    selected_sample_numbers.append(max_distance_sample_number)
    remaining_sample_numbers = np.arange(0, x_variables.shape[0], 1)
    x_variables = np.delete(x_variables, selected_sample_numbers, 0)
    remaining_sample_numbers = np.delete(remaining_sample_numbers, selected_sample_numbers, 0)
    for iteration in range(1, k):
        selected_samples = original_x[selected_sample_numbers, :]
        min_distance_to_selected_samples = list()
        for min_distance_calculation_number in range(0, x_variables.shape[0]):
            distance_to_selected_samples = ((selected_samples - np.tile(x_variables[min_distance_calculation_number, :],
                                                                        (selected_samples.shape[0], 1))) ** 2).sum(
                axis=1)
            min_distance_to_selected_samples.append(np.min(distance_to_selected_samples))
        max_distance_sample_number = np.where(
            min_distance_to_selected_samples == np.max(min_distance_to_selected_samples))
        max_distance_sample_number = max_distance_sample_number[0][0]
        selected_sample_numbers.append(remaining_sample_numbers[max_distance_sample_number])
        x_variables = np.delete(x_variables, max_distance_sample_number, 0)
        remaining_sample_numbers = np.delete(remaining_sample_numbers, max_distance_sample_number, 0)

    return selected_sample_numbers, remaining_sample_numbers

# 对样本进行预处理并画图
def plot_embedding(data, title):
    """
    :param data:数据集
    :param label:样本标签
    :param title:图像标题
    :return:图像
    """
    x_min, x_max = np.min(data, 0), np.max(data, 0)
    data = (data - x_min) / (x_max - x_min)  # 对数据进行归一化处理
    fig = plt.figure()  # 创建图形实例
    ax = plt.subplot(111)  # 创建子图
    # 遍历所有样本
    for i in range(data.shape[0]):
        # 在图中为每个数据点画出标签
        plt.text(data[i, 0], data[i, 1], str(0), color=plt.cm.Set1(0 / 10),
                 fontdict={'weight': 'bold', 'size': 7})
    plt.xticks()  # 指定坐标的刻度
    plt.yticks()
    plt.title(title, fontsize=14)
    # 返回值
    return fig

if __name__ == '__main__':
    np.random.seed(0)
    data = np.random.random((100,125))
    y = np.random.randint(0,5,(100,))

    number_of_selected_samples = 80
    idxs_selected_sample, idxs_remaining_sample = kennardstonealgorithm(data, number_of_selected_samples)

    data_slt = data[idxs_selected_sample]
    tsne = TSNE(n_components=2, init='pca', random_state=0)
    reslut = tsne.fit_transform(data_slt)

    fig = plot_embedding(reslut, 't-SNE Embedding of digits')
    plt.show()

五、参考链接

GitHub - hkaneko1985/kennardstonealgorithm: Sample selection using Kennard-Stone algorighm

KS算法、样本集划分