在探索排序算法的世界中,我们经常遇到需要对大量数据进行排序的情况。传统的插入排序虽然简单,但在处理大规模数据时效率并不高。这时,希尔排序(Shell Sort)就显得尤为重要。本文将通过深入解析希尔排序的逻辑,帮助读者更好地理解这一高效的排序方法。
希尔排序的基本概念
希尔排序,由Donald Shell于1959年提出,是插入排序的一种改进版本。它通过引入“间隔因子”来分组进行插入排序,有效地减少了数据交换和移动的次数。希尔排序的核心思想是将整个待排序的记录序列分割成若干个子序列分别进行直接插入排序。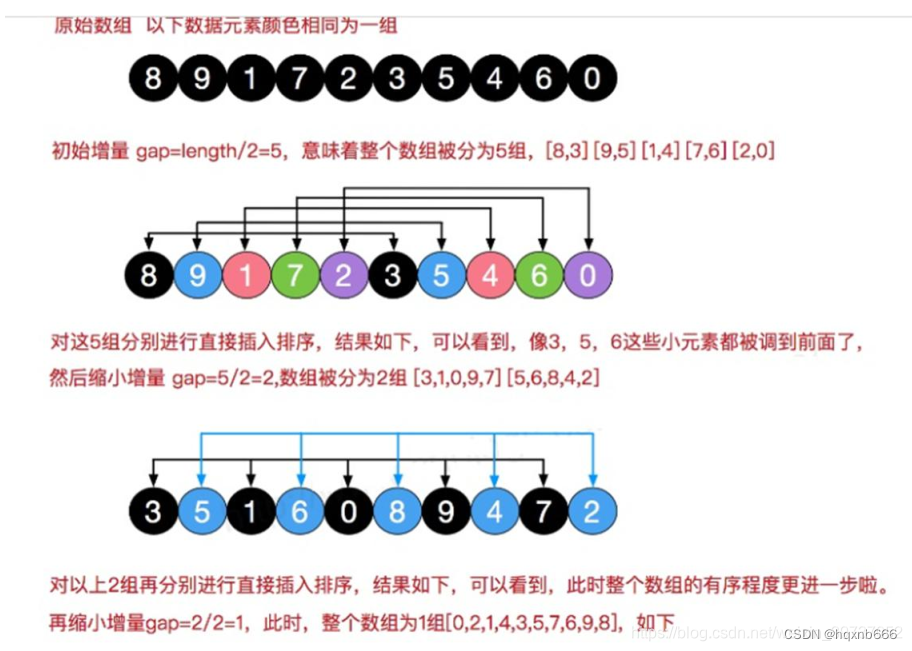
接下来,我们先从他的基础,插入排序讲解。
直接插入排序是一种简单的插入排序法,其基本思想是:
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为 止,得到一个新的有序序列 。 实际中我们玩扑克牌时,就用了插入排序的思想

当插入第i(i>=1)个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排序码与 array[i-1],array[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移
直接插入排序的特性总结:
1. 元素集合越接近有序,直接插入排序算法的时间效率越高
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1),它是一种稳定的排序算法
4. 稳定性:稳定
void InsertSort(int* a, int n)
{
for (int i = 0; i < n; i++)
{
int end = i;
int tmp = a[end + 1];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + 1] = a[end];
end--;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}探索希尔排序的代码逻辑
我们以C语言代码为例,详细解析希尔排序的实现过程:
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1; // 计算新的间隔
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end]; // 进行数据的交换
end -= gap; // 向前移动gap位置
}
else
{
break;
}
}
a[end + gap] = tmp; // 插入元素
}
}
}
在希尔排序中,我们可以将整个排序过程划分为“预排序”,和“直接插入排序”
预排序:分别对每个组进行插入排序

在上述代码中,我们采用嵌套关系来控制每一组进行预排序。也就是当<gap时,就有++j次的组进行预排序。所以gap就是组次
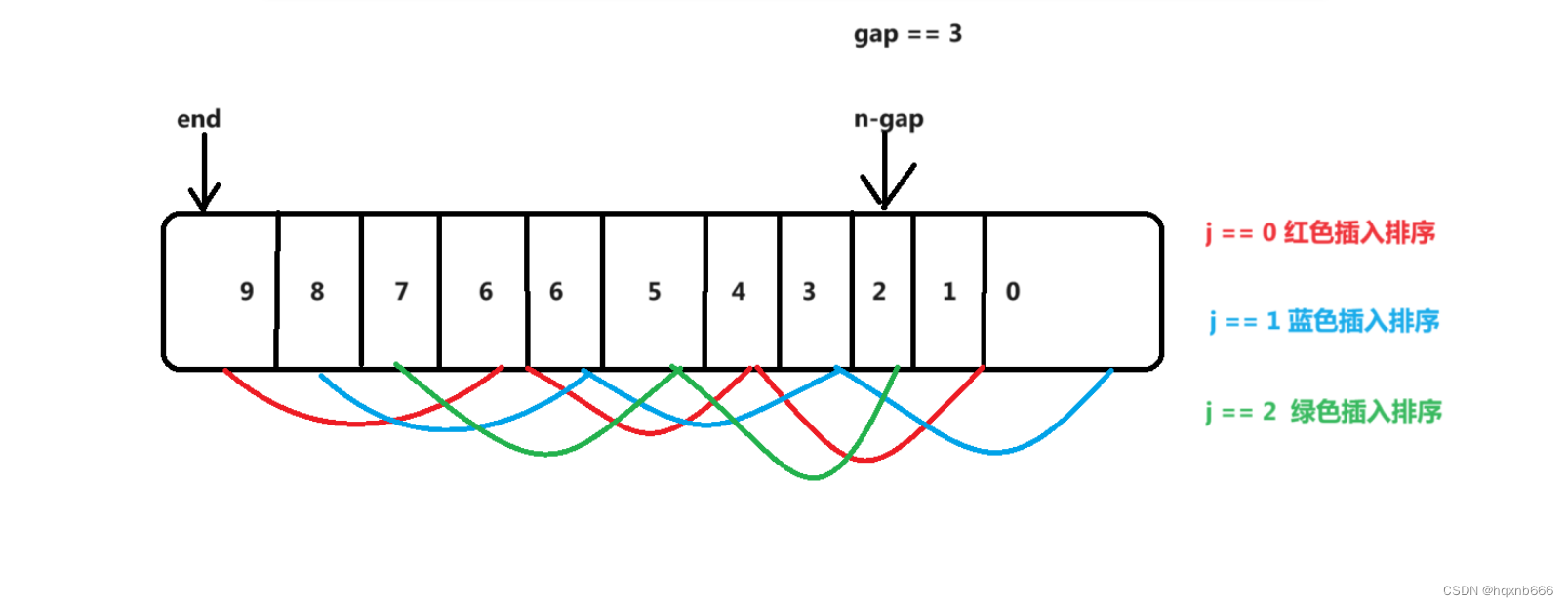
此时我们按照一组一组预排序,还需要外层嵌套for循环来控制,所以我们采用多组并排进行代码优化。

此时相当于我们走了第一个红色,紧接着不走红色这组,我们++i来到蓝色这组,蓝色也走一次,再来到绿色,以此类推。当我们走到n-gap时,就代表我们三组并排,直接走完
此时预排序已经走完,接下来就是到如何预排序完进行插入排序


所以gap的大小我们如何确定才能选择一个最为合适的gap呢,我们采用while循环.
和 ‘gap = gap/3 +1’ 当我们最开始进行预排序时,很快,但是不够接近有序,所以我们不断缩小gap,一开始有人提出用gap /2 ,确实可以,但又有人发现/3效率更高,但/3有可能为0,所以我们进行+1 ,确保最后gap一定能为1,所以此while循环不断进行,直到gap==1,进行插入排序,此时上一层预排序后已经十分接近升序序列,所以这一层的时间复杂度接近O(n),最后经过研究,最接近希尔排序的时间复杂度是N^1.13
我们采用Pop函数进行排序时间测试,排序代码见附录

可见希尔排序已经相对于冒泡和插入,已经十分优秀了。
间隔序列的选择
在此代码中,间隔序列是关键。初始时,gap 设置为数组长度,然后逐步减小(gap = gap / 3 + 1),直至减到1。这种递减的间隔序列可以帮助我们在排序初期迅速减少大量的逆序对,从而提高排序效率。
排序过程
在每一个固定的间隔下,代码通过插入排序的方式对分组数据进行排序。随着间隔的不断减小,整个数组越来越接近于完全有序,当间隔减小到1时,整个数组实际上已经接近于完全有序状态,此时进行一次插入排序后,数组即变为有序。
希尔排序的效率和应用
希尔排序的时间复杂度与间隔序列的选择有很大关系,最佳情况下的时间复杂度可以达到O(n^1.13)。由于其独特的排序方式,希尔排序在处理大规模乱序数组时,相较于传统的插入排序有着显著的效率优势。它不仅适用于普通的数据排序任务,还在某些特定类型的数据处理场景中表现出色。
希尔排序的优缺点
-
优点:
- 相较于传统的插入排序,在处理大量数据时有更高的效率。
- 算法结构简单,易于理解和实现。
- 适用于大型数据集,特别是对于初期无序的数据排序效果显著。
-
缺点:
- 间隔序列的选择对性能有很大影响,但最优的间隔序列尚无定论。
- 在最坏的情况下,性能可能并不理想。
- 相对于更高级的排序算法(如快速排序、归并排序等),在一些特定情况下仍然效率较低。
附录:
#define _CRT_SECURE_NO_WARNINGS
#include "Sort.h"
void TestOP()
{
srand(time(0));
const int N = 100000;
int* a1 = (int*)malloc(sizeof(int) * N);
int* a2 = (int*)malloc(sizeof(int) * N);
int* a3 = (int*)malloc(sizeof(int) * N);
int* a4 = (int*)malloc(sizeof(int) * N);
int* a5 = (int*)malloc(sizeof(int) * N);
int* a6 = (int*)malloc(sizeof(int) * N);
int* a7 = (int*)malloc(sizeof(int) * N);
for (int i = 0; i < N; ++i)
{
a1[i] = rand();
a2[i] = a1[i];
a3[i] = a1[i];
a4[i] = a1[i];
a5[i] = a1[i];
a6[i] = a1[i];
a7[i] = a1[i];
}
int begin1 = clock();
InsertSort(a1, N);
int end1 = clock();
int begin2 = clock();
ShellSort(a2, N);
int end2 = clock();
int begin3 = clock();
//SelectSort(a3, N);
int end3 = clock();
int begin4 = clock();
//HeapSort(a4, N);
int end4 = clock();
int begin5 = clock();
//QuickSort(a5, 0, N - 1);
int end5 = clock();
int begin6 = clock();
//MergeSort(a6, N);
int end6 = clock();
int begin7 = clock();
BubbleSort(a7, N);
int end7 = clock();
printf("InsertSort:%d\n", end1 - begin1);
printf("ShellSort:%d\n", end2 - begin2);
printf("SelectSort:%d\n", end3 - begin3);
printf("HeapSort:%d\n", end4 - begin4);
printf("QuickSort:%d\n", end5 - begin5);
printf("MergeSort:%d\n", end6 - begin6);
printf("BubbleSort:%d\n", end7 - begin7);
free(a1);
free(a2);
free(a3);
free(a4);
free(a5);
free(a6);
free(a7);
}
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void InsertSort(int* a, int n)
{
for (int i = 0; i < n; i++)
{
int end = i;
int tmp = a[end + 1];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + 1] = a[end];
end--;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}
void BubbleSort(int* a, int n)//使用bool来进阶冒泡 ,当有一层不交换,就代表已经排完序,防止永久时间复杂度都是O(n^2)
{
for (int j = 0; j < n; j++)
{
bool exange = false;
for (int i = 1; i < n - j; i++)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exange = true;
}
}
if (exange == false)
break;
}
}
void ShellSort(int* a, int n)
// gap > 1时是预排序,目的让他接近有序
// gap == 1是直接插入排序,目的是让他有序
{
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
希尔排序的特性总结:
1. 希尔排序是对直接插入排序的优化。
2. 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就 会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
3. 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些树中给出的 希尔排序的时间复杂度都不固定 
总结起来,希尔排序是一种高效且实用的排序算法,特别适用于大规模且初期无序的数据集。你的代码提供了一个很好的示例,展现了希尔排序的实现及其与其他排序算法相比的性能优势。希望这篇博客能帮助读者更好地理解和运用希尔排序算法。